Biết \(\frac{a}{2}=\frac{b}{3};\frac{a}{4}=\frac{c}{9}\) và \(^{a^3+b^3+c^3=-1009}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TT
0

TN
1

2 tháng 10 2015
a) Xem hình vẽ.
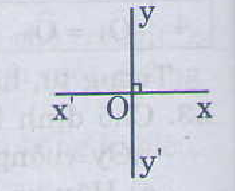
b)
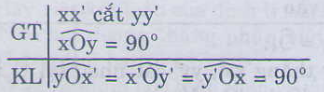
c) Điền vào chỗ trống:
1) (vì là hai góc kề bù).
2) (theo giả thiết và căn cứ vào 1).
3) (căn cứ vào 2).
4) (vì là hai góc đối đỉnh).
5) (căn cứ vào 4 và giả thiết).
6) (vì là hai góc đối đỉnh).
7) (căn cứ vào 6 và 3).
d)Trình bày lại cách chứng minh một cách gọn hơn.
Ta có: (hai góc kề bù) mà
(gt)
nên .
Suy ra
Lại có (hai góc đối đỉnh).
Suy ra .
TT
1

2 tháng 10 2015
\(\frac{2x-3y}{x+2y}=\frac{2}{3}\)
=> 3(2x-3y)=2(x+2y)
=> 6x-9y=2x+4y
=> 4x=13y
=> x/y=13/4
y/x=4/13
V
0

NT
1
\(\frac{a}{2}=\frac{b}{3}\Rightarrow\frac{a}{4}=\frac{b}{6}=\frac{c}{9}\)
\(\Rightarrow\frac{a^3}{4^3}=\frac{b^3}{6^3}=\frac{c^3}{9^3}=\frac{a^3+b^3+c^3}{64+216+729}=\frac{-1009}{1009}=-1\)
=>a3=-64=>a=-4
b3=216=>b=-6
c3=-729=>c=-9
Vậy (a;b;c)=(-4;-6;-9)
\(\frac{a}{2}=\frac{b}{3};\frac{a}{4}=\frac{c}{9}\)
suy ra: \(\frac{b}{12}=\frac{a}{8}=\frac{c}{18}suyra\frac{b^3}{1728}=\frac{a^3}{512}=\frac{c^3}{5832}\)
suy ra \(\frac{b^3+a^3+c^3}{1728+512+5832}=\frac{-1009}{8072}=\frac{-1}{8}\)
a/8= -1/8 suy ra a=-1
b/12=-1/8 suy ra b= -3/2
c/18=-1/8 suy ra c = -9/4
b/