HCl→CH3​CH2​Cl

\(\left(\right. 2 \left.\right) \left(C H\right)_{3} \left(C H\right)_{2} C l + N a O H \left(C H\right)_{3} \left(C H\right)_{2} O H + N a C l\)

\(\left(\right. 3 \left.\right) \left(C H\right)_{3} \left(C H\right)_{2} O H + C u O \left(C H\right)_{3} C H O + C u + H_{2} O\)

\(\left(\right. 4 \left.\right) \left(C H\right)_{3} C H O + \left(B r\right)_{2} + H_{2} O \rightarrow \left(C H\right)_{3} C O O H + 2 H B r\)

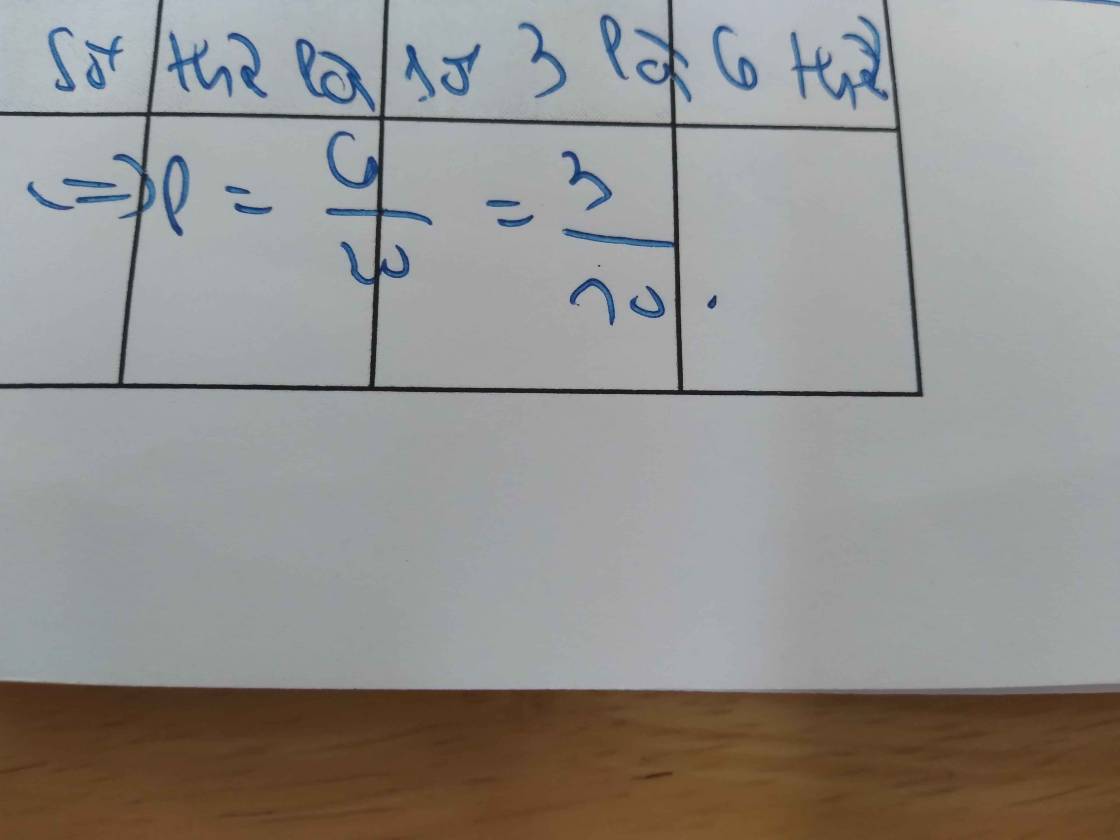
Có 6 khả năng rút được thẻ số 3 nên xác suất của biến cố "Thẻ rút ra là thẻ đánh số 3" là:

P = 6/20 = 3/10

\(Fe+2HCl→\:FeCl_2+H_2\)

  0,16       0,32          0,16         0,16

số mol Fe là:

\(n_{Fe}=\dfrac{m_{Fe}}{M_{Fe}}=\dfrac{8,96}{56}=0,16\left(mol\right)\)

thể tích khí H₂ thoát ra là:

\(V_{H_2}=24,79\cdot n_{H_2}=24,79\cdot0,16=3,9664\left(L\right)\)

=))

ummm......

cũng được!

(a) 2CH₃[CH₂]₄CHO + O₂  xt,to−→→xt,to 2CH₃[CH₂]₄COOH

hexanal                         hexanoic acid

(b) CH₃[CH₂]₆CHO + H_{2 Ni,to−−→→Ni,to} CH₃[CH₂]₆CH₂OH

octanal                          octan-1-ol

(c) CH₃CH₂COOH + CH₃OH  H2SO4dac,t°⇌⇌H2SO4dac,t° CH₃CH₂COOCH₃ + H₂O

     propanoic acid                        methanol     methyl propanoate

(d) CH₃CH₂-CO-CH₂CH₂CH₃ + H₂   Ni,to−−→→Ni,to  CH₃CH₂-CH(OH)-CH₂CH₂CH₃

        hexan-3-one                                    hexan-3-ol

(e) CH₃CH₂CH(CH₃)CH₂COOH + CH₃-CH(OH)-CH_{3  Ni,to−−→→Ni,to}

3-methylpentanoic acid         propan-2-ol

CH₃CH₂CH(CH₃)CH₂COOCH(CH₃)₂ + H₂O

isopropyl 3-methylpentanoate

(g) CH₃CH₂CH(CH₃)CHO + H₂   Ni,to−−→→Ni,to CH₃CH₂CH(CH₃)CH₂OH

         2-methylbutanal                            2-methylbutanol

(h) CH₃CH(CH₃)CH(CH₃)CH₂OH+O_{2 enzyme−−−→→enzyme}CH₃CH(CH₃)CH(CH₃)COOH + H₂O

2,3-dimethylbutan-1-ol                   2,3-dimethylbutanoic acid

Kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu là:

135,45-88,18=47,27(tỉ USD)

Kim ngạch xuất khẩu của Việt Nam với thị trường Mỹ là:

\(156,32\%\cdot47,27\simeq73,89\left(tỉUSD\right)\)

Kim ngạch xuất khẩu của Việt nam với thị trường châu Á nhiều hơn tổng 2 thị trường kia là:

135,45-(47,27+73,89)\(\simeq\)14,29(tỉ USD)

Kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu là:

135,45-88,18=47,27(tỉ USD)

Kim ngạch xuất khẩu của Việt Nam với thị trường Mỹ là:

$156,32\%\cdot 47,27\simeq 73,89\left(tỉ\; usd\right)$

Kim ngạch xuất khẩu của Việt nam với thị trường châu Á nhiều hơn tổng 2 thị trường kia là:

135,45-(47,27+73,89)$\simeq$14,29(tỉ USD)

Nước hóa rắn (tức là quá trình nước chuyển từ thể lỏng sang thể rắn) là một quá trình tỏa nhiệt

  đây ạ 

a) Xét $△ABC$ có �^+�^+�^=180∘A^+B^+C^=180∘ mà �^=90∘;�^=50∘A^=90∘;B^=50∘ suy ra 90∘+50∘+�^=180∘=>�^=40∘90∘+50∘+C^=180∘=>C^=40∘
b) Xét tam giác $△BEA$ và $△BEH$.
có $BE$ là cạnh chung
 ���^=���^(=90∘)��=�� suy  ra △���=△��� (c.h-cgv) ⇒���^=���^  suy ⇒​BAE=BHE(=90

a) Xét $△ABC$ có �^+�^+�^=180∘A^+B^+C^=180∘ mà �^=90∘;�^=50∘A^=90∘;B^=50∘ suy ra 90∘+50∘+�^=180∘=>�^=40∘90∘+50∘+C^=180∘=>C^=40∘
b) Xét tam giác $△BEA$ và $△BEH$.
có $BE$ là cạnh chung
 ���^=���^(=90∘)��=�� suy  ra △���=△��� (c.h-cgv) ⇒���^=���^  suy ⇒​BAE=BHE(=90