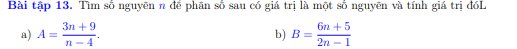
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(A=\dfrac{1,11+0,19-13.2}{2,06+0,54}-\left(\dfrac{1}{2}+\dfrac{1}{4}\right):2\\ =\dfrac{1,3-26}{2,6}-\dfrac{3}{4}.\dfrac{1}{2}\\ =\dfrac{1,3\left(1-20\right)}{1,3.2}-\dfrac{3}{8}\\ =\dfrac{-19}{2}-\dfrac{3}{8}=-\dfrac{79}{8}\)
\(B=\left(5\dfrac{7}{8}-2\dfrac{1}{4}-0,5\right):2\dfrac{23}{26}\\ =\left(5+\dfrac{7}{8}-2-\dfrac{1}{4}-0,5\right):\dfrac{75}{26}\\ =\left[\left(3-0,5\right)+\left(\dfrac{7}{8}-\dfrac{2}{8}\right)\right]:\dfrac{75}{26}\\ =\left(2,5+\dfrac{5}{8}\right):\dfrac{75}{26}\\ =\dfrac{25}{8}.\dfrac{26}{75}=\dfrac{13}{12}\)
b) Để \(A< x< B\) thì: \(-\dfrac{79}{8}< x< \dfrac{13}{12}\)
\(\Rightarrow x\in\left\{-9;-8;-7;...;1\right\}\) (do \(x\in\mathbb{Z}\))

a: \(3\cdot9\cdot\left(-27\right)=3\cdot3^2\cdot\left(-3^3\right)=-3^6\)
b: \(5\cdot25\cdot\left(-125\right)^2=5\cdot5^2\cdot\left(5^3\right)^2=5^9\)
c: \(0,5\cdot\left(-0,25\right)\cdot0,0625=0,5\cdot\left(-1\right)\cdot\left(0,5\right)^2\cdot\left(0,5\right)^4\)
\(=-\left(0,5\right)^7\)
d: \(2\cdot32\cdot\left(-1024\right)=2\cdot2^5\cdot\left(-1\right)\cdot2^{10}=-2^{16}\)
e: \(49\cdot7^3\cdot\left(-7\right)^3=7^2\cdot7^3\cdot\left(-1\right)\cdot7^3=-7^8\)
f: \(\dfrac{3}{4}\cdot\dfrac{9}{16}\cdot\dfrac{27}{64}=\dfrac{3}{4}\cdot\left(\dfrac{3}{4}\right)^2\cdot\left(\dfrac{3}{4}\right)^3=\left(\dfrac{3}{4}\right)^6\)
a, 3.9.27
= - 3.32.33
= - 31+2+3
= - 33+3
= - 36

1: \(\dfrac{-2}{3}+\dfrac{3}{4}-\dfrac{-1}{6}+\dfrac{-2}{5}\)
\(=-\dfrac{40}{60}+\dfrac{45}{60}+\dfrac{10}{60}-\dfrac{24}{60}\)
\(=\dfrac{5-14}{60}=-\dfrac{9}{60}=-\dfrac{3}{20}\)
2: \(\dfrac{-2}{3}+\dfrac{-1}{5}+\dfrac{3}{4}-\dfrac{5}{6}-\dfrac{-7}{10}\)
\(=\left(-\dfrac{2}{3}+\dfrac{3}{4}-\dfrac{5}{6}\right)+\left(-\dfrac{1}{5}+\dfrac{7}{10}\right)\)
\(=\left(-\dfrac{8}{12}+\dfrac{9}{12}-\dfrac{10}{12}\right)+\left(-\dfrac{2}{10}+\dfrac{7}{10}\right)\)
\(=\dfrac{-9}{12}+\dfrac{5}{10}=-\dfrac{3}{4}+\dfrac{1}{2}=-\dfrac{3}{4}+\dfrac{2}{4}=-\dfrac{1}{4}\)
3: \(\dfrac{1}{2}-\dfrac{-2}{5}+\dfrac{1}{3}+\dfrac{5}{7}-\dfrac{-1}{6}+\dfrac{-4}{35}+\dfrac{1}{41}\)
\(=\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}\right)+\left(\dfrac{2}{5}+\dfrac{5}{7}-\dfrac{4}{35}\right)+\dfrac{1}{41}\)
\(=\dfrac{3+2+1}{6}+\dfrac{14+25-4}{35}+\dfrac{1}{41}\)
\(=\dfrac{6}{6}+\dfrac{35}{35}+\dfrac{1}{41}=2+\dfrac{1}{41}=\dfrac{83}{41}\)
4: \(\dfrac{1}{100\cdot99}-\dfrac{1}{99\cdot98}-\dfrac{1}{98\cdot97}-...-\dfrac{1}{3\cdot2}-\dfrac{1}{2\cdot1}\)
\(=\dfrac{1}{100\cdot99}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{97\cdot98}+\dfrac{1}{98\cdot99}\right)\)
\(=\dfrac{1}{100\cdot99}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{98}-\dfrac{1}{99}\right)\)
\(=\dfrac{1}{99}-\dfrac{1}{100}-\dfrac{98}{99}=\dfrac{-97}{99}-\dfrac{1}{100}=\dfrac{-9799}{9900}\)
5: \(\dfrac{\left(\dfrac{3}{10}-\dfrac{4}{15}-\dfrac{7}{20}\right)\cdot\dfrac{5}{19}}{\left(\dfrac{1}{14}+\dfrac{1}{7}-\dfrac{-3}{35}\right)\cdot\dfrac{-4}{3}}=\dfrac{\dfrac{18-16-21}{60}\cdot\dfrac{5}{19}}{\dfrac{5+10+6}{70}\cdot\dfrac{-4}{3}}\)
\(=\dfrac{\dfrac{-19}{60}\cdot\dfrac{5}{19}}{\dfrac{21}{70}\cdot\dfrac{-4}{3}}=\dfrac{-5}{60}:\dfrac{-84}{210}=\dfrac{-1}{12}\cdot\dfrac{-5}{2}=\dfrac{5}{24}\)
6: \(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}+\dfrac{\dfrac{3}{5}-\dfrac{3}{25}-\dfrac{3}{125}-\dfrac{3}{625}}{\dfrac{4}{5}-\dfrac{4}{25}-\dfrac{4}{125}-\dfrac{4}{625}}\)
\(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4\left(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}\right)}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
\(=\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{4}{4}=1\)

Gọi mẫu số của phân số cần tìm là x
Theo đề, ta có: \(-\dfrac{11}{13}< \dfrac{9}{x}< \dfrac{-11}{15}\)
=>\(\dfrac{11}{13}>\dfrac{-9}{x}>\dfrac{11}{15}\)
=>\(\dfrac{99}{117}>\dfrac{-99}{11x}>\dfrac{99}{135}\)
=>\(\dfrac{99}{117}>\dfrac{99}{-11x}>\dfrac{99}{135}\)
=>\(-11x\in\left\{118;119;...;134\right\}\)
=>\(x\in\left\{-\dfrac{118}{11};-\dfrac{119}{11};...;\dfrac{134}{-11}\right\}\)
mà x nguyên
nên \(x\in\left\{-11;-12\right\}\)
Vậy: Hai phân số cần tìm là \(\dfrac{9}{-11};\dfrac{9}{-12}\)
=>

\(\dfrac{a}{d}+\dfrac{c}{d}=\dfrac{a}{b}\cdot\dfrac{c}{d}\\ =>\dfrac{a}{b}\cdot\dfrac{c}{d}-\dfrac{c}{d}=\dfrac{a}{b}\\ =>\dfrac{c}{d}\cdot\left(\dfrac{a}{b}-1\right)=\dfrac{a}{b}\\ =>\dfrac{c}{d}\cdot\dfrac{a-b}{b}=\dfrac{a}{b}\\ =>\dfrac{c}{d}=\dfrac{a}{b}:\dfrac{a-b}{b}\\ =>\dfrac{c}{d}=\dfrac{a}{b}\cdot\dfrac{b}{a-b}\\ =>\dfrac{c}{d}=\dfrac{a}{a-b}\)
Vậy: ...

a) Để A là phân số thì \(n-2\ne0\Rightarrow n\ne2\)
b) \(A=-3=>\dfrac{2n-7}{n-2}=-3\)
\(=>2n-7=-3\left(n-2\right)\\ =>2n-7=-3n+6\\ =>2n+3n=6+7\\ =>5n=13\\ =>n=\dfrac{13}{5}\left(ktm\right)\)
c) \(A=\dfrac{2n-7}{n-2}=\dfrac{2n-4-3}{n-2}=\dfrac{2\left(n-2\right)-3}{n-2}=2-\dfrac{3}{n-2}\)
Để A nguyên thì: 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ={1; -1; 3; -3}
=> n ∈ {3; 1; 5; -1}
d) Để A lớn nhất thì \(\dfrac{3}{n-2}\) nhỏ nhất
=> \(\dfrac{3}{n-2}=-1\)
=> 3 = -(n - 2)
=> 3 = -n + 2
=> n = -1
e) Để A nhỏ nhất thì \(\dfrac{3}{n-2}\) lớn nhất
=> \(\dfrac{3}{n-2}=1\)
=> 3 = n - 2
=> n = 3 + 2
=> n = 5
f) Để A là phân số tối giản => ƯCLN(2n - 7; n - 2) = 1
=> ƯCLN(3; n - 2) = 1
=> n - 2 không chia hết cho 3
=> n - 2 ≠ 3k
=> n ≠ 3k + 2
g) Gọi d là ước nguyên tố của 2n - 7 và n - 2 ta có:
2n - 7 ⋮ d và n - 2 ⋮ d
=> 2n - 7 ⋮ d và 2(n - 2) ⋮ d
=> (2n - 4) - (2n - 7) ⋮ d
=> 3 ⋮ d
=> d ∈ {1; -1; 3; -3}
Mà d là STN => d = 3
Với d = 3 => 2n - 7 ⋮ 3 => 2(2n - 7) ⋮ 3 => 4n - 7 ⋮ 3
=> 3n + n - 7 ⋮ 3
=> n - 7 ⋮ 3
=> n - 7 = 3k
=> n = 3k + 7
bạn cho mình hỏi sao câu d và câu e lại là -1 và 1 thế ạ?

c; C = \(\dfrac{28^{28}+28^{24}+...+28^4+1}{28^{30}+28^{28}+...+28^2+1}\)
A = 1 + 284 + 288 + 2812 + ...2828
284A = 284 + 288 + 2812 + ... + 2828 + 2832
284A - A = 284+ 288+...+2828+ 2832- (1 + 284 + 288+...+2828)
(284 - 1)A = 284 + 288+ ...+ 2828 + 2832 - 1 - 284- ...- 2828
(284 - 1)A = (2832 - 1) + (284 - 284) + (288 - 288) + ... + (2828 - 2828)
(284 - 1)A = 2832 - 1 + 0 + 0... + 0
A = (2832 - 1): (284 - 1)
Đặt B = 2830 + 2828 + ... + 282 + 1
282B = 2832 + 2830 + ... + 284 + 282
282B - B = 2832 + 2830 + ... + 284 + 282 - (2830 + 2828 +...+1)
(282 - 1)B = 2832 + 2830+...+284 + 282 - 2830 - 2828 - ... 282- 1
(282 - 1)B = (2832 - 1) + (2830 - 2830) +...+(282 - 282)
(282 - 1)B = (2832 - 1) + 0 + 0 +...+ 0
(282 - 1)B = 2832 - 1
B = (2832 - 1): (282 - 1)
C = \(\dfrac{A}{B}\) = \(\dfrac{28^{32}-1}{28^4-1}\) : \(\dfrac{28^{32}-1}{28^2-1}\)
C = \(\dfrac{28^{32}-1}{28^4-1}\) \(\times\) \(\dfrac{28^2-1}{28^{32}-1}\)
C = \(\dfrac{28^2-1}{28^4-1}\)
C = \(\dfrac{1}{785}\)
Câu d:
\(\dfrac{x-1}{99}\) + \(\dfrac{x-2}{98}\) + \(\dfrac{x-3}{97}\) = \(\dfrac{x-4}{96}\) + \(\dfrac{x-5}{95}\) + \(\dfrac{x-6}{94}\)
(\(\dfrac{x-1}{99}\)-1)+(\(\dfrac{x-2}{98}\)-1)+(\(\dfrac{x-3}{97}\)-1) = (\(\dfrac{x-4}{96}\)-1) + (\(\dfrac{x-5}{95}\)-1)+(\(\dfrac{x-6}{94}\)-1)
\(\dfrac{x-100}{99}\)+\(\dfrac{x-100}{98}\)+\(\dfrac{x-100}{97}\) = \(\dfrac{x-100}{96}\)+\(\dfrac{x-100}{95}\)+\(\dfrac{x-100}{94}\)
\(\dfrac{x-100}{99}\)+\(\dfrac{x-100}{98}\)+\(\dfrac{x-100}{97}\)- \(\dfrac{x-100}{96}\)-\(\dfrac{x-100}{95}\)-\(\dfrac{x-100}{94}\) = 0
(\(x-100\)).(\(\dfrac{1}{99}\)+\(\dfrac{1}{98}\)+\(\dfrac{1}{97}\) - \(\dfrac{1}{96}\)-\(\dfrac{1}{95}\)-\(\dfrac{1}{94}\)) = 0
Vì\(\dfrac{1}{98}< \dfrac{1}{98}< \dfrac{1}{97}< \dfrac{1}{96}< \dfrac{1}{95}< \dfrac{1}{94}\)
Nên (\(\dfrac{1}{99}\) + \(\dfrac{1}{98}\) + \(\dfrac{1}{97}\) )- (\(\dfrac{1}{96}\) + \(\dfrac{1}{95}\) +\(\dfrac{1}{94}\) )< 0
⇒\(x-100\) = 0
Vậy \(x\) = 100

Ta có: QE\(\perp\)OM
NP\(\perp\)OM
Do đó: QE//NP
Ta có: PQ\(\perp\)Ox
MN\(\perp\)Ox
Do đó: PQ//MN

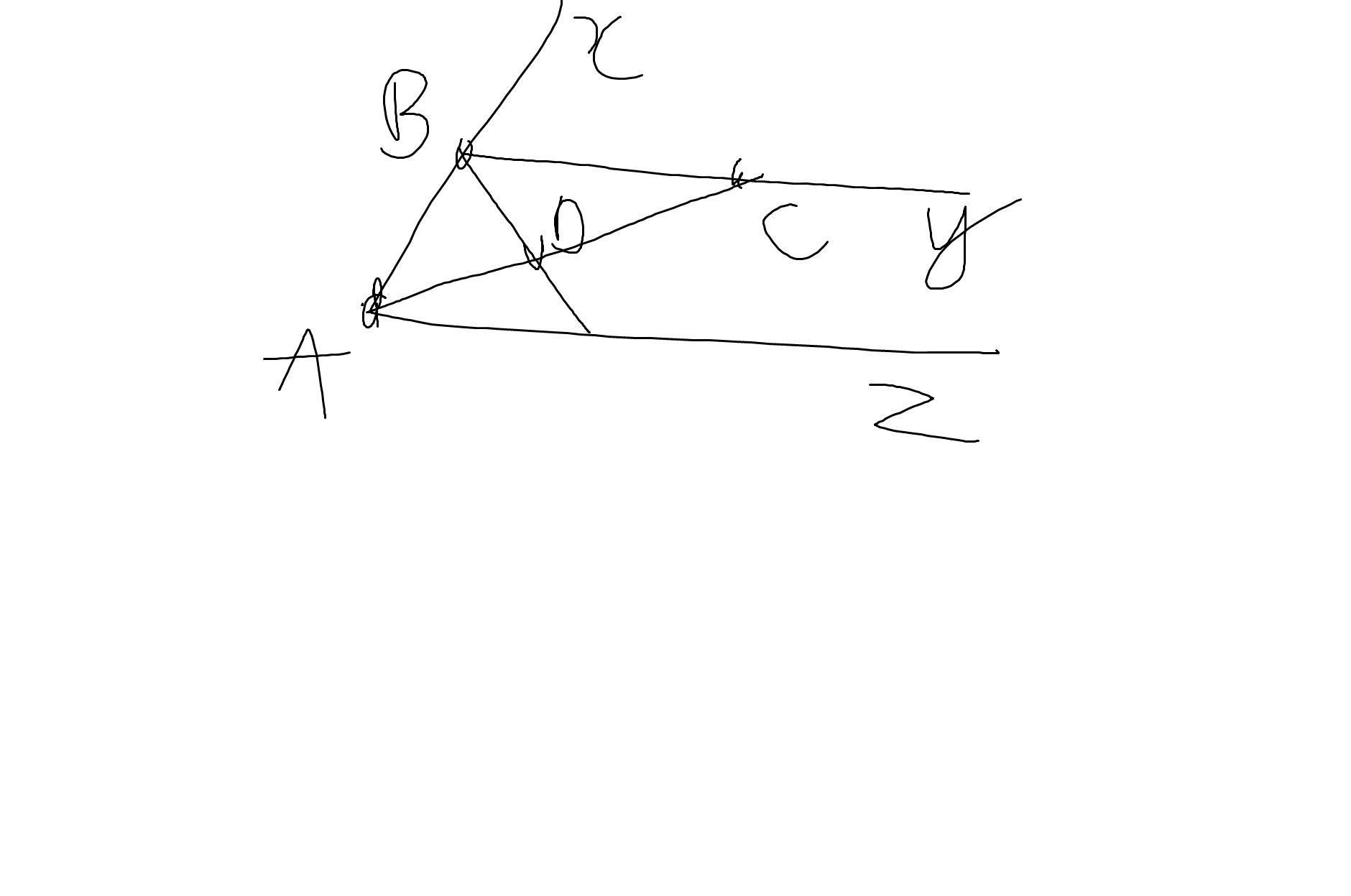
a: Ta có: \(\widehat{xBy}=\widehat{xAz}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên By//Az
b: Ta có: \(\widehat{ABC}+\widehat{xBC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABC}+60^0=180^0\)
=>\(\widehat{ABC}=120^0\)
AC là phân giác của góc zAB
=>\(\widehat{BAC}=\dfrac{\widehat{xAB}}{2}=30^0\)
Xét ΔBAC có \(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^0\)
=>\(\widehat{BCA}+120^0+30^0=180^0\)
=>\(\widehat{BCA}=30^0\)
c: Ta có: BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=60^0\)
Xét ΔDBA có \(\widehat{DBA}+\widehat{DAB}=60^0+30^0=90^0\)
nên ΔBDA vuông tại D
=>BD\(\perp\)AC
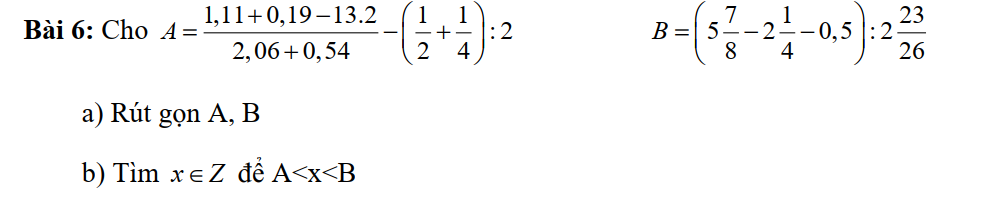



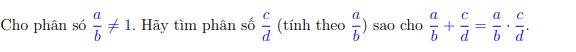
 Help!
Help!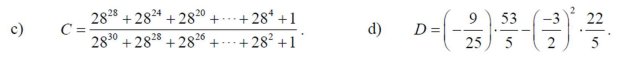
 Giúp mình với các bạn,mình cần gấp câu c1 và câu d2 ạ !
Giúp mình với các bạn,mình cần gấp câu c1 và câu d2 ạ !

a: ĐKXĐ: \(n\ne4\)
Để A là số nguyên thì \(3n+9⋮n-4\)
=>\(3n-12+21⋮n-4\)
=>\(21⋮n-4\)
=>\(n-4\in\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
=>\(n\in\left\{5;3;7;1;11;-3;25;-17\right\}\)
b: ĐKXĐ: \(n\ne\dfrac{1}{2}\)
Để B là số nguyên thì \(6n+5⋮2n-1\)
=>\(6n-3+8⋮2n-1\)
=>\(8⋮2n-1\)
=>\(2n-1\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
mà 2n-1 lẻ(do n là số nguyên)
nên \(2n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{1;0\right\}\)