Cho tam giác ABC vuông tại A, đường phân giác trong BE, EC = 3, BC = 6. Tính độ dài các đoạn thẳng AB, AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi tam giác cân là ABC (cân tại A), đường cao AH.
Gọi cạnh đáy của tam giác cân là a, cạnh bên là b. Theo đề bài:
10a = 12b
=> a/b = 6/5
Đặt a = 6k, b = 5k
Xét tam giác AHC vuông tại H:
AH^2 + HC^2 = AC^2
<=> 10^2 + a^2/4 = b^2
<=> a^2/4 = b^2 - 100
<=> (6k)^2/4 = (5k)^2 - 100
<=> 9k^2 = 25k^2 - 100
<=> 16k^2 = 100 <=> k = 10/4
=> a = 6k = 6.10/4 = 15 (cm)
=> S_ABC = 1/2BC.AH = 1/2a.10 = 5a = 5.15 = 75 (cm^2)
1012ABCDExy
Đặt CD=x,CD=x, AC=yAC=y.
Ta có: 10.x=6.y10.x=6.y (=SABC=SABC)
Suy ra xy=35xy=35.
Đặt x=3t,x=3t, y=5ty=5t.
Áp dụng định lí Pi-ta-go vào tam giác vuông ACDACD tìm được t=2t=2.
Vậy x=6,x=6, SABC=60cm2SABC=60cm2.

* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
mà \(\frac{AB}{AC}=\frac{5}{6}\Rightarrow AB=\frac{5}{6}AC\Rightarrow AB^2=\left(\frac{5}{6}AC\right)^2\)
hay \(\frac{1}{900}=\frac{1}{\left(\frac{5}{6}AC\right)^2}+\frac{1}{AC^2}\Rightarrow AC=6\sqrt{55}\)
\(\Rightarrow AB=\frac{5}{6}.6\sqrt{55}=5\sqrt{55}\)
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow BC=\frac{AB.AC}{AH}=\frac{1650}{30}=\frac{165}{3}\)
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{1375}{\frac{165}{3}}=\frac{25}{9}\)
* Áp dụng hệ thức : \(AC^2=HC.BC\Rightarrow HC=\frac{AC^2}{BC}=\frac{1980}{\frac{165}{3}}=4\)
Ta có: \(\dfrac{AB}{AC}\)=\(\dfrac{5}{6}\)
⇒ \(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.HC}=\dfrac{BH}{CH}=\dfrac{x}{y}=\dfrac{25}{36}\)
Đặt x= 25z, y= 36z
ΔABC vuông tại H có:
AH2= BH.HC ( Py-ta-go)
⇔302= 25z.36z
⇔900z2= 900
⇔z2= 1
⇔z=1
Vậy x=25, y=36

tam giác ABC vuông tại A có AT là đường cao
Áp dụng định lí Py ta go ta có : \(AB^2+AC^2=BC^2\Rightarrow25-AB^2=AC^2\)(1)
* Theo hệ thức : \(\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AT^2}\Rightarrow\frac{1}{4}=\frac{1}{AB^2}+\frac{1}{25-AB^2}\)( theo 1 )
\(\Rightarrow AB=2\sqrt{5};\sqrt{5}\)
TH1 : \(25-\left(2\sqrt{5}\right)^2=AC\Rightarrow AC=\sqrt{5}\)
TH2 : \(25-\left(\sqrt{5}\right)^2=AC\Rightarrow AC=2\sqrt{5}\)
Gọi BH là z ( z>0), thì HC là 5-z
ΔABC vuông tại A có:
AH.BC=BH.HC (định lý 3)
⇔ 22 = z(5-z)
⇔ z2 - 5z + 4 = 0
⇔ z(z-1) - 4(z-1) = 0
⇔(z-4)(z-1)=0
⇔\(\left[{}\begin{matrix}z-4=0\\z-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}z=4\left(nhận\right)\\z=1\left(nhận\right)\end{matrix}\right.\)
TH1:Nếu z=4
ΔABC vuông tại A có:
x2=BC.BH ( định lý 1)
⇔ x2= 5.4
⇔ x2= 20
⇒x=\(2\sqrt{5}\)
ta có: y2= BC.HC ( định lý 1)
Chứng minh tương tự như trên ta được
y= \(\sqrt{5}\)
TH2: Nếu z=1
Chứng minh tương tự như TH1 ta được:
x=\(\sqrt{5}\)
y= \(2\sqrt{5}\)

Xét tam giác ABC vuông tại A, có AH là đường cao
Áp dụng định lí Py ta go ta có :
\(BC^2=AB^2+AC^2=36+64=100\Rightarrow BC=10\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{36}{10}=\frac{18}{5}\)
hay \(x=\frac{18}{5}\)cm
* Áp dụng hệ thức : \(AC^2=HC.BC\Rightarrow HC=\frac{AC^2}{BC}=\frac{64}{10}=\frac{32}{5}\)
hay \(y=\frac{32}{5}\)cm
xét tam giác ABC ,ta có:
theo định lí py-ta-go :
BC=x+y=\(\sqrt{AB^2+AC^2}\)=\(\sqrt{6^2+8^2}\)=\(\sqrt{100}\)=10
\(6^2\)=10*x\(\Rightarrow\)x=\(\dfrac{6^2}{10}\)\(\Leftrightarrow\)x=3,6
y+x=10\(\Leftrightarrow\)y=10-3,6\(\Leftrightarrow\)y=6,4

Xét tam giác ABC vuông tại A, có đường cao AH
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=400-144=256\Rightarrow AC=16\)
* Áp dụng hệ thức : \(AC^2=HC.BC\Rightarrow HC=\frac{AC^2}{BC}=\frac{256}{20}=\frac{89}{5}\)
hay \(y=\frac{89}{5}\)
*Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{144}{20}=\frac{36}{5}\)
hay \(x=\frac{36}{5}\)
\(12^2\)=20*x\(\Rightarrow\)x=\(\dfrac{12^2}{20}\)=7,2;
x+y=20\(\Leftrightarrow\)y=20-x\(\Leftrightarrow\)y=20-7,2\(\Leftrightarrow\)y=12,8

ΔABH vuông tại H có:
AH2 = AB2 - y2 ( Py-ta-go)
⇔BH.HC = AB2 - y2
⇔ 32y = 302 - y2
⇔ 32y + y2 - 900 = 0
⇔ 50y + y2 -18y - 900 = 0
⇔ y(50 + y) - 18( y + 50) = 0
⇔(y -18)(50+y)= 0
⇔\(\left[{}\begin{matrix}y-18=0\\50+y=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}y=18\left(nhận\right)\\y=-50\left(loại\right)\end{matrix}\right.\)
ΔABC vuông tại A có:
x2= BC2 - AB2 ( py-ta-go)
⇔x2= (18 + 32)2 - 302
⇔x2= 1600
⇒x=40
* Áp dụng hệ thức : \(AB^2=BH.BC\)( mà \(BC=BH+HC=BH+32\))
\(\Rightarrow BH=\frac{900}{BH+32}\Rightarrow BH=18\)
hay \(y=18\)
* Áp dụng hệ thức : \(AC^2=HC.BC\)( mà \(BC=HC+BH=32+18=40\))
\(\Rightarrow AC^2=32.40=1280\Rightarrow AC=16\sqrt{5}\)
hay \(x=16\sqrt{5}\)

Áp dụng định lí Py ta go ta có : \(AC^2=AH^2+HC^2\Rightarrow AH^2=AC^2-HC^2\)
\(=100-64=36\Rightarrow AH=6\)cm
* Áp dụng hệ thức \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AB^2}=\frac{1}{AH^2}-\frac{1}{AC^2}\)
\(=\frac{1}{36}-\frac{1}{100}=\frac{100-36}{3600}=\frac{64}{3600}\Rightarrow AB^2=\frac{3600}{64}\Rightarrow AB=\frac{15}{2}\)
hay \(x=\frac{15}{2}\)cm
* Áp dụng hệ thức : \(AH^2=BH.HC\Rightarrow BH=\frac{AH^2}{HC}=\frac{36}{8}=\frac{9}{2}\)
hay \(y=\frac{9}{2}\)cm


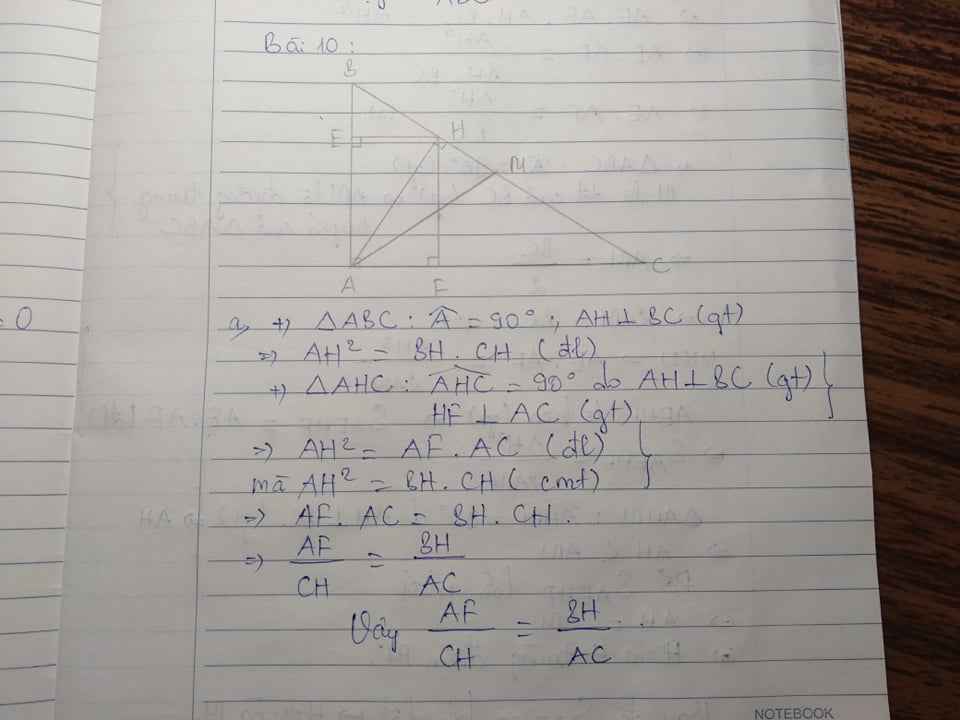
BE là đường phân giác
=> AE/EC=AB/BC
=> AB=AE.BC/EC=6AE/3=2EC
có AB^2+AC^2=BC^2
<=>4AE^2+AE^2+2AE.AC+EC^2=BC^2
<=>5AE^2+6AE+9=36
<=> 5AE^2+6AE-27=0
<=> [AE=1,8
[AE=-3(loại)
=> AC=4,8 cm
AB=3,6 cm
A B C E 3 6
Xét tam giác ABC vuông tại A , BE là đường phân giác
\(\Rightarrow\frac{AB}{BC}=\frac{AE}{EC}\)mà : \(AB^2+AC^2=BC^2\Rightarrow AB^2=BC^2-AC^2\Rightarrow AB=\sqrt{36-AC^2}\)
\(AE=AC-EC=AC-3\)
\(\Rightarrow\frac{\sqrt{36-AC^2}}{6}=\frac{AC-3}{3}\)
\(\Rightarrow\frac{36-AC^2}{36}=\frac{\left(AC-3\right)^2}{9}\Rightarrow AC=\frac{24}{5}\)
Áp dụng định lí Py ta go ta có :
\(AB^2+AC^2=BC^2\Rightarrow AB^2=BC^2-AC^2=36-\frac{576}{25}=\frac{324}{25}\)
\(\Rightarrow AB=\frac{18}{5}\)