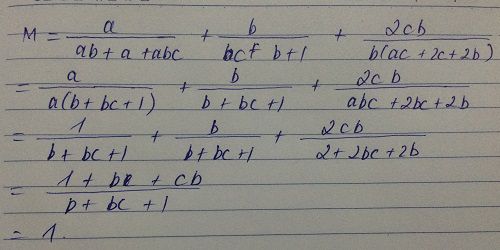Kẻ \(CH//AG\)và các điểm như hình vẽ. 

Trong tam giác \(BCF\): \(\widehat{FBC}+\widehat{BCF}+\widehat{CFB}=180^o\). 

Trong tam giác \(ADE\): \(\widehat{DAE}+\widehat{DEA}+\widehat{ADE}=180^o\)

\(BC//AD\Rightarrow\widehat{FBC}=\widehat{EDA}\)(Hai góc so le trong) 

\(CH//AG\Rightarrow\widehat{CFB}=\widehat{AED}\)(Hai góc so le trong) 

Suy ra \(\widehat{BCF}=\widehat{DAE}\).

Xét tam giác \(DAE\)và tam giác \(BCF\)có: 

\(\widehat{BCF}=\widehat{DAE}\)(cmt)

\(DA=BC\)(tính chất hình bình hành)

\(\widehat{CBF}=\widehat{ADE}\)(cmt)

Suy ra \(\Delta DAE=\Delta BCF\). 

Suy ra \(DE=BF\)(hai cạnh tương ứng). 

Có: \(\frac{DG}{GC}=\frac{DE}{EF}=\frac{DE}{EB-BF}=\frac{DE}{EB-DE}\Rightarrow\frac{GC}{DG}=\frac{EB-DE}{DE}=4-1=3\Rightarrow\frac{DG}{GC}=\frac{1}{3}\)

Ta có: \(M=\frac{1}{\left(x-2\right).\left(x-3\right)}+\frac{1}{\left(x-3\right).\left(x-4\right)}+\frac{1}{\left(x-4\right).\left(x-5\right)}+\frac{1}{\left(x-5\right).\left(x-6\right)}\)

   \(\Leftrightarrow M=\frac{1}{x-2}-\frac{1}{x-3}+\frac{1}{x-3}-\frac{1}{x-4}+\frac{1}{x-4}-\frac{1}{x-5}+\frac{1}{x-5}-\frac{1}{x-6}\)

   \(\Leftrightarrow M=\frac{1}{x-2}-\frac{1}{x-6}\)

   \(\Leftrightarrow M=\frac{x-6-x+2}{\left(x-2\right).\left(x-6\right)}\)

   \(\Leftrightarrow M=-\frac{4}{x^2-8x+12}\)

tau đéo biết

Vì \(abc=2\)nên ta có:

\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)

\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)

\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(1+bc+b\right)}\)

\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+c+1}\)

\(=\frac{1+b+bc}{bc+c+1}=1\)

câu trả lời;

ĐKXĐ : x ≠ ±1

pt <=> \(\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}-\frac{4}{\left(x-1\right)\left(x+1\right)}=0\)

<=> \(\frac{x^2+2x+1-x^2+2x-1-4}{\left(x-1\right)\left(x+1\right)}=0\)

<=> \(\frac{4x-4}{\left(x-1\right)\left(x+1\right)}=0\)

=> 4x - 4 = 0 

<=> x = 1 ( ktm )

Vậy phương trình vô nghiệm 

Gọi h(x) là thương trong phép chia f(x) cho g(x)

Vì f(x) bậc 3, g(x) bậc 2 => h(x) bậc nhất

=> h(x) có dạng cx + d

f(x) ⋮ g(x) <=> f(x) = g(x).h(x)

<=> x³ + ax² + 2x + b = ( x² + x + 1 )( cx + d )

<=> x³ + ax² + 2x + b = cx³ + dx² + cx² + dx + cx + d

<=> x³ + ax² + 2x + b = cx³ + ( d + c )x² + ( d + c )x + d

Đồng nhất hệ số ta có :

\(\hept{\begin{cases}c=1\\d+c=a=2\\d=b\end{cases}}\Rightarrow\hept{\begin{cases}a=2\\b=c=d=1\end{cases}}\)

Vậy a = 2 , b = 1

Vì \(f \left(x\right)⋮g\left(x\right)\)\(\Rightarrow\)\(f\left(x\right)=g\left(x\right).Q\left(x\right)\)     

Đặt \(Q\left(x\right)=cx+d\)          \(\left(c,d\ne0\right)\)

\(\Rightarrow\)\(f\left(x\right)=\left(x^2+x+1\right).\left(cx+d\right)\)

\(\Leftrightarrow\)\(f\left(x\right)=cx^3+dx^2+cx^2+dx+cx+d\)

\(\Leftrightarrow\)\(x^3+ax^2+2x+b=cx^3+\left(d+c\right)x+\left(d+c\right)x+d\)

Đồng nhất hệ số, ta có:

      \(c=1\)                                             \(a=2\)

      \(d+c=a\)              \(\Leftrightarrow\)           \(b=1\)

      \(d+c=2\)                                    \(c=1\)\(\left(TM\right)\)

      \(d=b\)                                             \(d=1\)\(\left(TM\right)\)

Vậy \(f \left(x\right)⋮g\left(x\right)\)khi  \(\hept{\begin{cases}a=2\\b=1\end{cases}}\)

Ta có: \(P=\sqrt{x+2}+\sqrt{4-x}\)

\(\Leftrightarrow P^2=\left(\sqrt{x+2}+\sqrt{4-x}\right)^2\) , áp dụng bất đẳng thức Bunyakovsky ta có:

\(P^2\le\left(1^2+1^2\right)\left[\left(\sqrt{x+2}\right)^2+\left(\sqrt{4-x}\right)^2\right]\)

\(=2\left(x+2+4-x\right)=2\cdot6=12\)

\(\Rightarrow P\le2\sqrt{3}\)

Dấu "=" xảy ra khi: \(x+2=4-x\Leftrightarrow x=1\)

Vậy \(Max\left(P\right)=2\sqrt{3}\Leftrightarrow x=1\)