Nửa chu vi hình chữ nhật là 120:2=60(m)

Gọi chiều rộng hình chữ nhật là x(m)

(ĐIều kiện: x>0)

Chiều dài hình chữ nhật là x+20(m)

Nửa chu vi là 60m nên ta có:

x+x+20=60

=>2x=40

=>x=40:2=20(nhận)

=>Chiều dài hình chữ nhật là 20+20=40(m)

Diện tích hình chữ nhật là \(20\cdot40=800\left(m^2\right)\)

a: Xét ΔABD vuông tại A và ΔDAK vuông tại D có

\(\widehat{ABD}=\widehat{DAK}\left(=90^0-\widehat{ADB}\right)\)

Do đó: ΔABD~ΔDAK

b: Ta có: ΔABD vuông tại A

=>\(AB^2+AD^2=BD^2\)

=>\(BD^2=12^2+5^2=169=13^2\)

=>BD=13(cm)

ΔABD~ΔDAK

=>\(\dfrac{BD}{AK}=\dfrac{AB}{DA}\)

=>\(\dfrac{13}{AK}=\dfrac{12}{5}\)

=>\(AK=13\cdot\dfrac{5}{12}=\dfrac{65}{12}\left(cm\right)\)

x² - 2x = 8

x² - 2x - 8 = 0

x² - 2x + 1 - 9 = 0

(x² - 2x + 1) - 9 = 0

(x - 1)² - 3² = 0

(x - 1 - 3)(x - 1 + 3) = 0

(x - 4)(x + 2) = 0

⇒ x - 4 = 0 hoặc x + 2 = 0

*) x - 4 = 0

x = 4

*) x + 2 = 0

x = -2

Vậy x = -2; x = 4

Gọi x là số thứ nhất

⇒ Số thứ hai là: 59 - x

Theo đề bài, ta có phương trình:

2x - 3(59 - x) = -7

2x - 177 + 3x = -7

5x = -7 + 177

5x = 170

x = 170 : 5

x = 34

Vậy số thứ nhất là 34

số thứ hai là 59 - 34 = 25

34 và 25.

giúp mình với nhé mình đang cần ngay bây giờ

oke

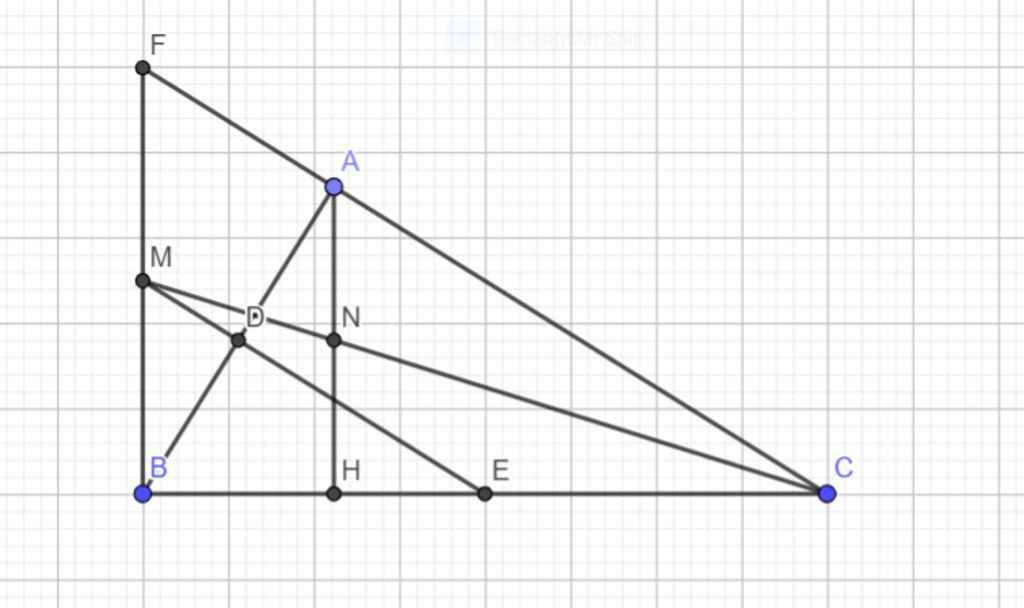
a: ΔABC vuông tại A

=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(1\right)\)

ΔABC có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(2\right)\)

Từ (1) và (2) suy ra \(AB\cdot AC=AH\cdot BC\)

b: Xét ΔABC có

D,E lần lượt là trung điểm của BA,BC

=>DE là đường trung bình của ΔABC

=>DE//AC và DE=1/2AC

=>AC=2DE

Xét ΔCHA vuông tại H và ΔCAB vuông tại A có

\(\widehat{HCA}\) chung

Do đó: ΔCHA~ΔCAB

=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)

=>\(CH\cdot CB=CA^2=4DE^2\)

a) \(P=\left(\dfrac{x^2-2}{x^2+2x}+\dfrac{1}{x+2}\right):\dfrac{x+1}{x}\left(x\ne\left\{0;-2;-1\right\}\right)\\ =\left[\dfrac{x^2-2}{x\left(x+2\right)}+\dfrac{1}{x+2}\right].\dfrac{x}{x+1}\\ =\dfrac{x^2-2+x}{x\left(x+2\right)}.\dfrac{x}{x+1}\\ =\dfrac{\left(x+2\right)\left(x-1\right)}{x\left(x+2\right)}.\dfrac{x}{x+1}\\ =\dfrac{x-1}{x+1}\)

b) \(P=\dfrac{5}{2}\Rightarrow\dfrac{x-1}{x+1}=\dfrac{5}{2}\\ \Rightarrow2\left(x-1\right)=5\left(x+1\right)\\ \Leftrightarrow2x-2=5x+5\\ \Leftrightarrow5x-2x=-2-5\\ \Leftrightarrow3x=-7\\ \Leftrightarrow x=-\dfrac{7}{3}\left(TMDK\right)\)

Vậy : x=-7/3 thì P=5/2

c) \(P=\dfrac{x-1}{x+1}=\dfrac{x+1-2}{x+1}\\ =1-\dfrac{2}{x+1}\)

Để P nhận gt nguyên => 2/x+1 đạt gt nguyên

=> 2 chia hết cho x+1

=> x+1 thuộc Ư(2)={1;-1;2;-2}

=> x thuộc {0;-2;1;-3}

Đối chiếu đk : x khác {0;-2;-1}

Kết luận : x thuộc {1;-3} là 2 giá trị nguyên của x thỏa mãn P nguyên

a: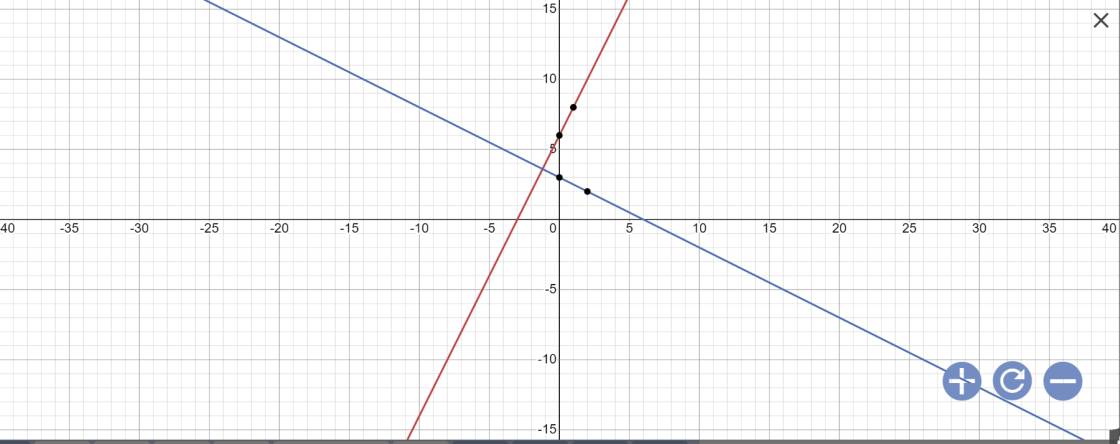 

b: Phương trình hoành độ giao điểm là:

\(2x+6=-\dfrac{1}{2}x+3\)

=>\(\dfrac{5}{2}x=-3\)

=>\(x=-3:\dfrac{5}{2}=-\dfrac{6}{5}\)=-1,2

Thay x=-1,2 vào y=2x+6, ta được:

\(y=2\cdot\left(-1,2\right)+6=3,6\)

vậy: C(-1,2;3,6)

c: Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\2x+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=0\end{matrix}\right.\)

vậy: A(-3;0); B(6;0); C(-1,2;3,6)

\(AB=\sqrt{\left(6+3\right)^2+\left(0-0\right)^2}=9\)

\(AC=\sqrt{\left(-1,2+3\right)^2+\left(3,6-0\right)^2}=\dfrac{9\sqrt{5}}{5}\)

\(BC=\sqrt{\left(-1,2-6\right)^2+\left(3,6-0\right)^2}=\dfrac{18\sqrt{5}}{5}\)

Vì \(AC^2+BC^2=AB^2\)

nên ΔABC vuông tại C

=>\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{9}{\sqrt{5}}\cdot\dfrac{18}{\sqrt{5}}=\dfrac{81}{5}\)

d: (d2): y=-1/2x+3

=>\(-\dfrac{1}{2}x-y+3=0\)

\(d\left(M;\left(d2\right)\right)=\dfrac{\left|0\cdot\left(-\dfrac{1}{2}\right)+\left(-3\right)\cdot\left(-1\right)+3\right|}{\sqrt{\left(-\dfrac{1}{2}\right)^2+\left(-1\right)^2}}=6:\dfrac{\sqrt{5}}{2}=\dfrac{12}{\sqrt{5}}\)

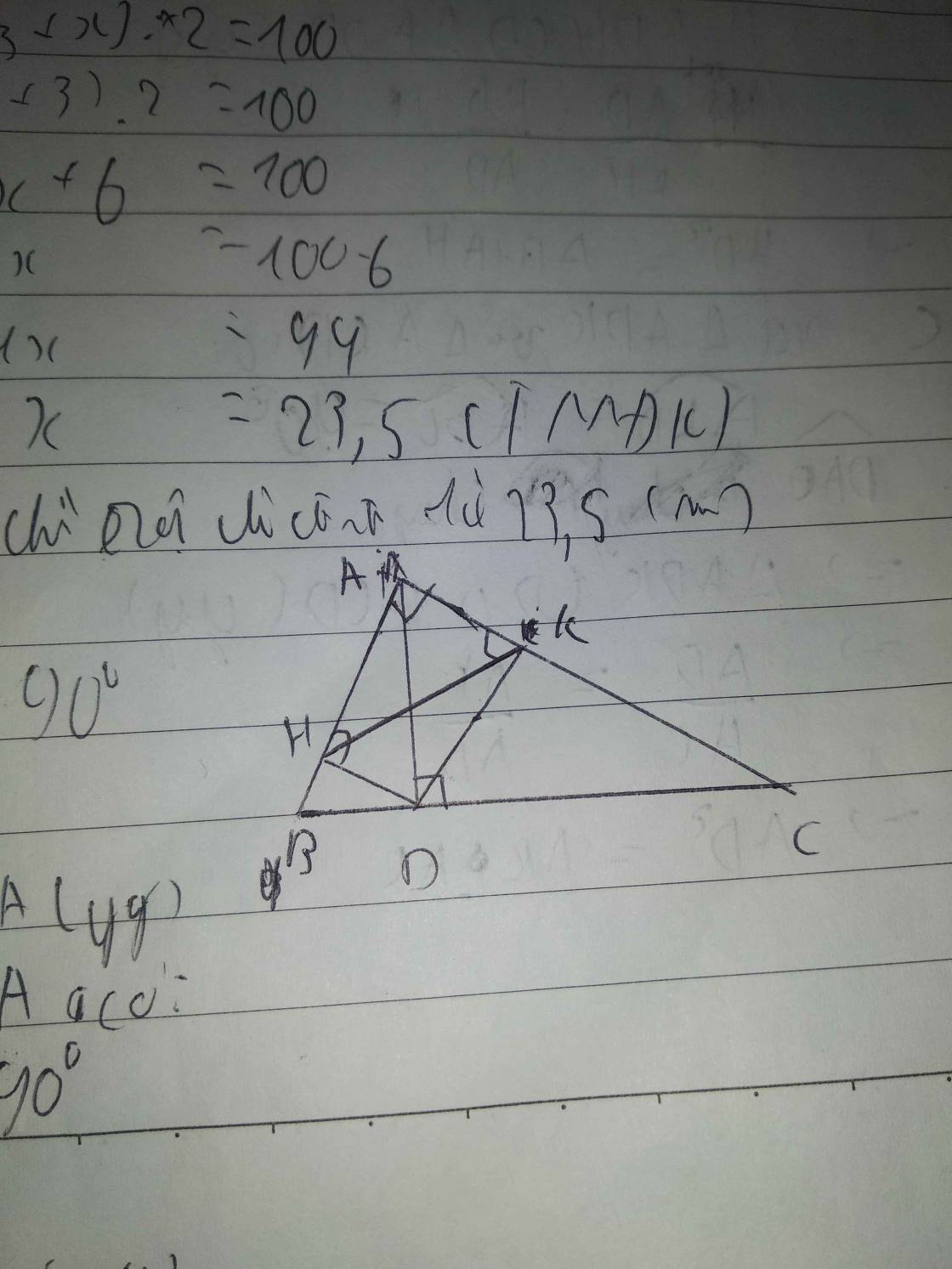
Xét ΔADB vuông tại D có DH là đường cao

nên \(AH\cdot AB=AD^2\left(1\right)\)

Xét ΔADC vuông tại D có DK là đường cao

nên \(AK\cdot AC=AD^2\left(2\right)\)

Từ (1) và (2) suy ra \(AH\cdot AB=AK\cdot AC\)

=>\(\dfrac{AH}{AC}=\dfrac{AK}{AB}\)

Xét ΔAHK vuông tại A và ΔACB vuông tại A có

\(\dfrac{AH}{AC}=\dfrac{AK}{AB}\)

Do đó: ΔAHK~ΔACB

a) \(A=\left(\dfrac{3x^2+3}{x^3-1}-\dfrac{x-1}{x^2+x+1}-\dfrac{1}{x-1}\right):\dfrac{2x^2-5x+5}{x-1}\left(x\ne1\right)\)

\(=\left[\dfrac{3x^2+3}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\right]\cdot\dfrac{x-1}{2x^2-5x+5}\)

\(=\dfrac{3x^2+3-\left(x-1\right)^2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x-1}{2x^2-5x+5}\)

\(=\dfrac{2x^2-x+2-\left(x^2-2x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x-1}{2x^2-5x+5}\)

\(=\dfrac{2x^2-x+2-x^2+2x-1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x-1}{2x^2-5x+5}\)

\(=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x-1}{2x^2-5x+5}\)

\(=\dfrac{1}{2x^2-5x+5}\)

b) Ta có: \(A=\dfrac{1}{2x^2-5x+5}=\dfrac{1}{2\left(x^2-\dfrac{5}{2}x+\dfrac{5}{2}\right)}\)

\(=\dfrac{1}{2\left(x^2-2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}-\dfrac{25}{16}+\dfrac{5}{2}\right)}\)

\(=\dfrac{1}{2\left[\left(x^2-2\cdot\dfrac{5}{4}+\dfrac{25}{16}\right)+\dfrac{15}{16}\right]}\)

\(=\dfrac{1}{2\left(x-\dfrac{5}{4}\right)^2+\dfrac{15}{8}}\)

Mà: \(2\left(x-\dfrac{5}{4}\right)^2\ge0\forall x\ne1\)

\(\Rightarrow2\left(x-\dfrac{5}{4}\right)^2+\dfrac{15}{8}\ge\dfrac{15}{8}\forall x\ne1\)

\(\Rightarrow\dfrac{1}{2\left(x-\dfrac{5}{4}\right)^2+\dfrac{15}{8}}\le\dfrac{8}{15}\forall x\ne1\) 

Dấu "=" xảy ra khi: \(\left(x-\dfrac{5}{4}\right)^2=0\Leftrightarrow x=\dfrac{5}{4}\)

Vậy: \(A_{max}=\dfrac{8}{15}\Leftrightarrow x=\dfrac{5}{4}\)