
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
Khi $x=1$ thì: $A=\frac{1}{\sqrt{1}+4}=\frac{1}{1+4}=\frac{1}{5}$
b. \(B=\frac{2(\sqrt{x}+3)-(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}-\frac{12}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{\sqrt{x}+9}{(\sqrt{x}-3)(\sqrt{x}+3)}-\frac{12}{(\sqrt{x}-3)(\sqrt{x}+3)}\)
\(=\frac{\sqrt{x}+9-12}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{\sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{1}{\sqrt{x}+3}\)
Ta có đpcm.
c. Với mọi $x\geq 0$ và $x\neq 9$ thì: $\sqrt{x}\geq 0\Rightarrow \sqrt{x}+3\geq 3$
$\Rightarrow B=\frac{1}{\sqrt{x}+3}\leq \frac{1}{3}< \frac{1}{2}$
Ta có đpcm.

Có: \(\left\{{}\begin{matrix}x^2+2y+1=0\\y^2+2z+1=0\\z^2+2x+1=0\end{matrix}\right.\)
\(\Rightarrow x^2+2y+1+y^2+2z+1+z^2+2x+1=0\)
\(\Rightarrow\left(x^2+2x+1\right)+\left(y^2+2y+1\right)+\left(z^2+2z+1\right)=0\)
\(\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2+\left(z+1\right)^2=0^{\left(1\right)}\)
Lại có:
\(\left\{{}\begin{matrix}\left(x+1\right)^2\ge0\forall x\\\left(y+1\right)^2\ge0\forall y\\\left(z+1\right)^2\ge0\forall z\end{matrix}\right.\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2+\left(z+1\right)^2\ge0\forall x;y;z^{\left(2\right)}\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x+1=0\\y+1=0\\z+1=0\end{matrix}\right.\Rightarrow x=y=z=-1\)
Thay \(x=y=z=-1\) vào \(A\), ta được:
\(A=\left(-1\right)^{2000}+\left(-1\right)^{2000}+\left(-1\right)^{2000}\)
\(=1+1+1=3\)
\(\text{#}\mathit{Toru}\)

a, với d = -1
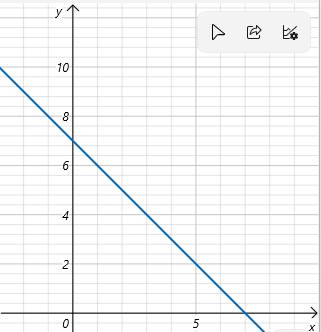
Ta có hàm số y = - \(x\) + 4 + 3 ⇒ y = -\(x\) + 7
+ Giao của đồ thị với trục o\(x\) là điểm có hoành độ thỏa mãn:
- \(x\) + 7 = 0 ⇒ \(x\) = 7
Giao đồ thì với trục o\(x\) là A(7; 0)
+ Giao của đồ thị với trục oy là điểm có tung độ thỏa mãn:
y = 0 + 7 ⇒ y = 7
Giao đồ thị với trục oy là điểm B(7; 0)
Ta có đồ thị
b, Đồ thị hàm số y = - m\(x\) + 4 - 3m (d)
(d) đi qua gốc tọa độ khi và chỉ tọa độ O(0; 0) thỏa mãn phương trình đường thẳng d
Thay tọa độ điểm O vào đường thẳng d ta có:
-m.0 + 4 - 3m = 0
4 - 3m = 0
m = \(\dfrac{4}{3}\)
c, để d cắt trục tung tại điểm - 4 khi và chỉ m thỏa mãn phương trình:
-m.0 + 4 - 3m = - 4
4 - 3m = - 4
3m = 8
m = \(\dfrac{8}{3}\)
d, d cắt trục tung tại điểm - 2 khi và chỉ khi m thỏa mãn phương trình
-m.0 + 4 - 3m = -2
4 - 3m = -2
3m = 6
m = 2
e, d song song với đường thẳng y = 2\(x\) + 3 khi và chỉ khi
- m = 2 và 4 - 3m ≠ 3 ⇒ m ≠ \(\dfrac{1}{3}\)
⇒m = -2
f, d đi qua A (1;2) khi và chỉ m thỏa mãn phương trình:
-m.(1) + 4 - 3m = 2
-m - 3m = 2 - 4
- 4m = -2
m = \(\dfrac{1}{2}\)

Bạn chỉ cần cho \(n\) lẻ thì \(p^{n+1}\) chính phương rồi nhé.

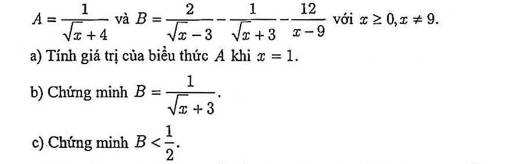
Ảnh bé và mờ quá. Bạn nên gõ hẳn đề lên để mọi người hỗ trợ tốt hơn nhé.