cho hình vuông ABCD cạnh 60. LẤy M, N, P trên AB, BC, CD sao cho MA=30, NB=20, PD=15. Gọi F là giao điểm ND và MP. tính diện tích tam giác MNF.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 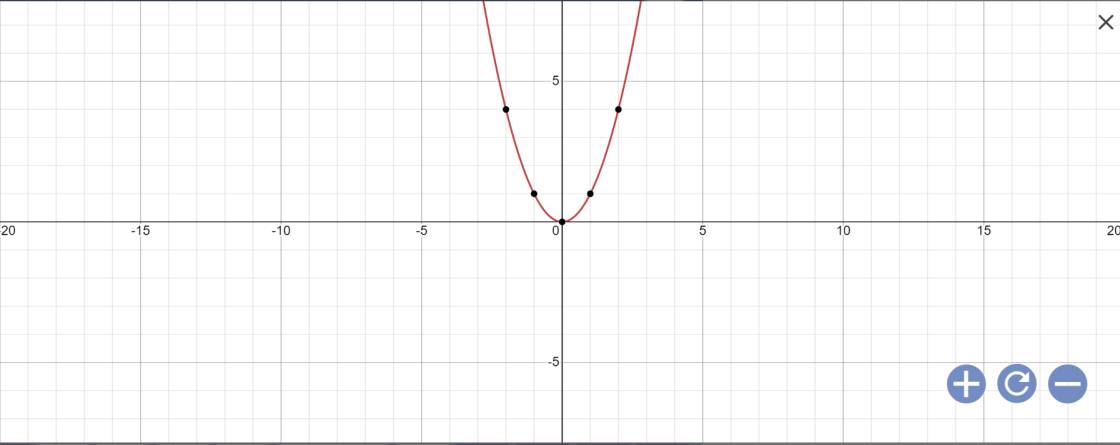
b: Phương trình hoành độ giao điểm là:
\(x^2=\left(m-2\right)x+6\)
=>\(x^2-\left(m-2\right)x-6=0\)
\(a\cdot c=1\cdot\left(-6\right)=-6< 0\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m-2\\x_1x_2=\dfrac{c}{a}=-6\end{matrix}\right.\)
\(x_2^2-x_1x_2+\left(m-2\right)x_1=16\)
=>\(x_2^2+x_1\left(x_1+x_2\right)-x_1x_2=16\)
=>\(x_2^2+x_1^2=16\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2=16\)
=>\(\left(m-2\right)^2-2\cdot\left(-6\right)=16\)
=>\(\left(m-2\right)^2=4\)
=>\(\left[{}\begin{matrix}m-2=2\\m-2=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=4\\m=0\end{matrix}\right.\)

Một hình bình hành có chiều cao là 9cm và bằng 3/4 độ dài đáy. Diện tích hình bình hành đó là 108 cm vuông
Độ dài đáy là 9:3/4=12(cm)
Diện tích hình bình hành là 9x12=108(cm2)

Xét tam giác AEB và tam giác CFD ta có
AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt)
Vậy tam giác AEB = tam giác CFD ( c.g.c )
=> AE = FC ( 2 cạnh tương ứng ) (1)
tương tự với tam giác AFD = tam giác EBC
=> AF = EC (2)
Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF
Xét tam giác AEB và tam giác CFD ta có
AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt)
Vậy tam giác AEB = tam giác CFD ( c.g.c )
=> AE = FC ( 2 cạnh tương ứng ) (1)
tương tự với tam giác AFD = tam giác EBC
=> AF = EC (2)
Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF



a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔNAI và ΔNCK có
\(\widehat{NAI}=\widehat{NCK}\)(AI//CK)
NA=NC
\(\widehat{ANI}=\widehat{CNK}\)(hai góc đối đỉnh)
Do đó: ΔNAI=ΔNCK
=>NI=NK
c: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của CB
Xét ΔABC có
AH,BN là các đường trung tuyến
AH cắt BN tại I
Do đó: I là trọng tâm của ΔABC
=>BI=2IN
mà IK=2IN
nên BI=IK
=>I là trung điểm của BK
Ta có: KC//AH
AH\(\perp\)BC
Do đó: KC\(\perp\)CB
=>ΔKCB vuông tại C
ΔCKB vuông tại C
mà CI là đường trung tuyến
nên IC=IK=IB
Xét ΔKBC có
KH,CI là các đường trung tuyến
KH cắt CI tại G
Do đó: G là trọng tâm của ΔKBC
=>IG=1/3IC
mà IC=IK
nên \(IG=\dfrac{1}{3}IK\)

Giải:
Vì a : 6 dư 2 ⇒ a + 10 ⋮ 6
a : 11 dư 1 ⇒ a + 10 ⋮ 11
⇒ a + 10 ⋮ 6 và 11
6 = 2.3; 11 = 11; BCNN(6; 11) = 2.3.11 = 66
⇒ a + 10 ⋮ 66
Vậy a chia 66 dư 10

Giải:
Nửa chu vi hình chữ nhật là: 54 x 2 = 108 (dm)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Chiều rộng của thửa ruộng hình chữ nhật là:
108 : (3 + 5) x 3 = 40,5 (dm)
Chiều dài của thửa ruộng là:
108 - 40,5 = 67,5 (dm)
Diện tích thửa ruộng là:
67,5 x 40,5 = 2733,75 (dm2)
Đáp số:..
Chu vi miếng đất hình vuông là:
54 x 4 = 216 (dm)
Nửa chu vi thửa ruộng HCN là:
216 : 2 = 108 (dm)
Chiều rộng thửa ruộng HCN là:
108 : (3+5) x 3 = 40,5 (dm)
Chiều dài thửa ruộng HCN là:
108 - 40,5 = 67,5 (dm)
Diện tích thửa ruộng HCN là:
40,5 x 67,5 = 2733,75 (dm2)
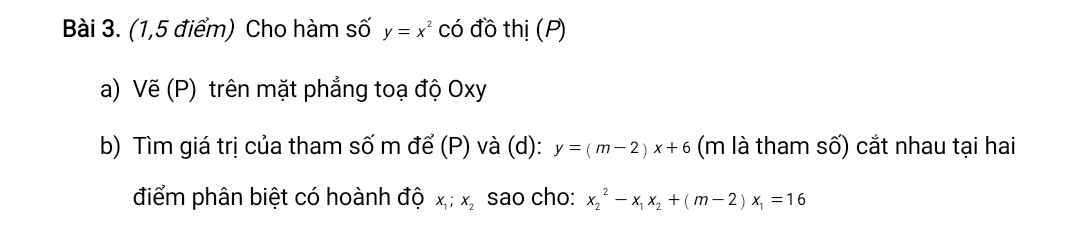

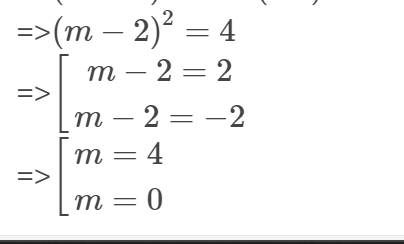
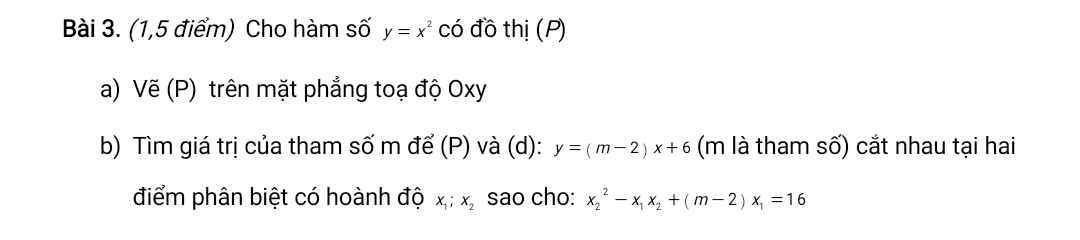

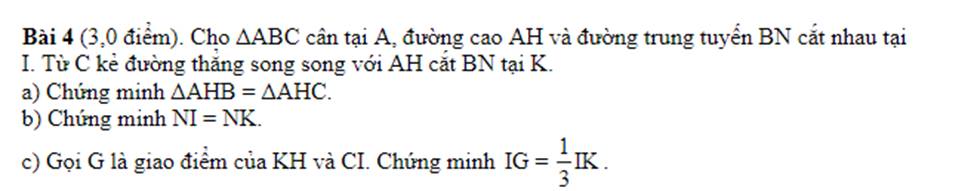

Đặt AM=NC=x��=��=�
Vì {AM//NCAM=NC⇒AMCN��//����=��⇒���� là hình bình hành ⇒SAMNC=60x⇒�����=60�
Vì SAMCN=SABCD⇒60x=6028⇔x=7,5(cm)�����=�����⇒60�=6028⇔�=7,5��
Vậy M cách A 7,5cm,7,5��,N cách C 7,5cm