
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\notin\left\{0;-3\right\}\)
\(\dfrac{3}{x+3}-\dfrac{x+6}{x^2+3x}\)
\(=\dfrac{3}{x+3}-\dfrac{x+6}{x\left(x+3\right)}\)
\(=\dfrac{3x-x-6}{x\left(x+3\right)}=\dfrac{2x-6}{x\left(x+3\right)}\)

ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(\dfrac{4}{x-3}+\dfrac{2}{x+3}\)
\(=\dfrac{4\left(x+3\right)+2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{4x+12+2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{6x+6}{\left(x-3\right)\left(x+3\right)}\)

ĐKXĐ: \(x\ne-\dfrac{3}{2}\)
\(\dfrac{5x}{2x+3}-\dfrac{x+4}{2x+3}=\dfrac{5x-x-4}{2x+3}=\dfrac{4x-4}{2x+3}\)

gọi chiều dài,chiều rộng là:a,b
Theo bài
(a+4)(b+2)-ab=8
ab+4b+2a+8-ab=8
2a+4b+8=8
Nửa chu vi là:36:2=18
=>36+2b+8=8
44+2b=8
2b=8-44
2b=-36
b=-18
=>a là : 36
em nghĩ bài này chx chắc nên anh tham khảo

Nửa chu vi mảnh vườn là:
36:2=18(m)
Gọi chiều dài mảnh vườn là x(m)
(ĐK: 0<x<18)
Chiều rộng mảnh vườn là 18-x(m)
Chiều dài khi tăng thêm 4m là x+4(m)
Chiều rộng khi giảm đi 2m là 18-x-2=16-x(m)
Diện tích tăng thêm 8m2 nên ta có:
(x+4)(16-x)-x(18-x)=8
=>\(16x-x^2+64-4x-18x+x^2=8\)
=>-6x=8-64=-56
=>\(x=\dfrac{56}{6}=\dfrac{28}{3}\left(nhận\right)\)
Vậy: Chiều dài mảnh vườn là 28/3(m)
Chiều rộng mảnh vườn là \(18-\dfrac{28}{3}=\dfrac{26}{3}\left(m\right)\)

a: Gọi giao điểm của d với CB là K
ta có: MK\(\perp\)AC
AB\(\perp\)AC
Do đó: MK//AB
Xét ΔCAB có
M là trung điểm của CA
MK//AB
Do đó: K là trung điểm của BC
Xét ΔABC có
M,K lần lượt là trung điểm của CA,CB
=>MK là đường trung bình của ΔABC
=>\(MK=\dfrac{1}{2}AB=MN\)
=>M là trung điểm của KN
Xét tứ giác ANCK có
M là trung điểm chung của AC và NK
=>ANCK là hình bình hành
Hình bình hành ANCK có CA\(\perp\)NK
nên ANCK là hình thoi
=>CA là phân giác của góc NCB
Xét ΔABC vuông tại A và ΔMNC vuông tại M có
\(\widehat{ACB}=\widehat{MCN}\)
Do đó: ΔABC~ΔMNC
b: Xét ΔCMN vuông tại M và ΔCAD vuông tại A có
\(\widehat{MCN}\) chung
Do đó: ΔCMN~ΔCAD

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB~ΔOCD
b: Sửa đề: cắt BC tại N
Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)
=>\(OM\cdot AC=DC\cdot AO\)
c: Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BO}{BD}\left(2\right)\)
Ta có: ΔOAB~ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra OM=ON
=>O là trung điểm của MN

1: \(x^4+3x^2-4=0\)
=>\(x^4+4x^2-x^2-4=0\)
=>\(\left(x^2+4\right)\left(x^2-1\right)=0\)
=>\(x^2-1=0\)
=>\(x^2=1\)
=>\(x=\pm1\)
2: \(\left(x^2-2x\right)^2+\left|x^2-2x\right|-2=0\)
=>\(\left(\left|x^2-2x\right|\right)^2+\left|x^2-2x\right|-2=0\)
=>\(\left(\left|x^2-2x\right|+2\right)\left(\left|x^2-2x\right|-1\right)=0\)
=>\(\left|x^2-2x\right|-1=0\)
=>\(\left[{}\begin{matrix}x^2-2x=1\\x^2-2x=-1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x^2-2x-1=0\\x^2-2x+1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(x-1\right)^2-2=0\\\left(x-1\right)^2=0\end{matrix}\right.\)
=>\(x\in\left\{1;\pm\sqrt{2}+1\right\}\)
3: ĐKXĐ: \(x\notin\left\{-2;-1\right\}\)
\(\dfrac{x}{x+2}< \dfrac{x}{x+1}\)
=>\(\dfrac{x}{x+2}-\dfrac{x}{x+1}< 0\)
=>\(\dfrac{x\left(x+1\right)-x\left(x+2\right)}{\left(x+2\right)\left(x+1\right)}< 0\)
=>\(\dfrac{-x}{\left(x+2\right)\left(x+1\right)}< 0\)
=>\(\dfrac{x}{\left(x+1\right)\left(x+2\right)}>0\)
TH1: \(\left\{{}\begin{matrix}x>0\\\left(x+1\right)\left(x+2\right)>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>0\\\left[{}\begin{matrix}x>-1\\x< -2\end{matrix}\right.\end{matrix}\right.\)
=>\(x>0\)
TH2: \(\left\{{}\begin{matrix}x< 0\\\left(x+1\right)\left(x+2\right)< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 0\\-2< x< -1\end{matrix}\right.\)
=>-2<x<-1
1.
$x^4+3x^2-4=0$
$\Leftrightarrow (x^4-x^2)+(4x^2-4)=0$
$\Leftrightarrow x^2(x^2-1)+4(x^2-1)=0$
$\Leftrightarrow (x^2-1)(x^2+4)=0$
$\Leftrightarrow x^2-1=0$ hoặc $x^2+4=0$
Nếu $x^2-1=0\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1$
Nếu $x^2+4=0\Leftrightarrow x^2=-4<0$ (vô lý)
Vậy pt có nghiệm $x=1$ hoặc $x=-1$


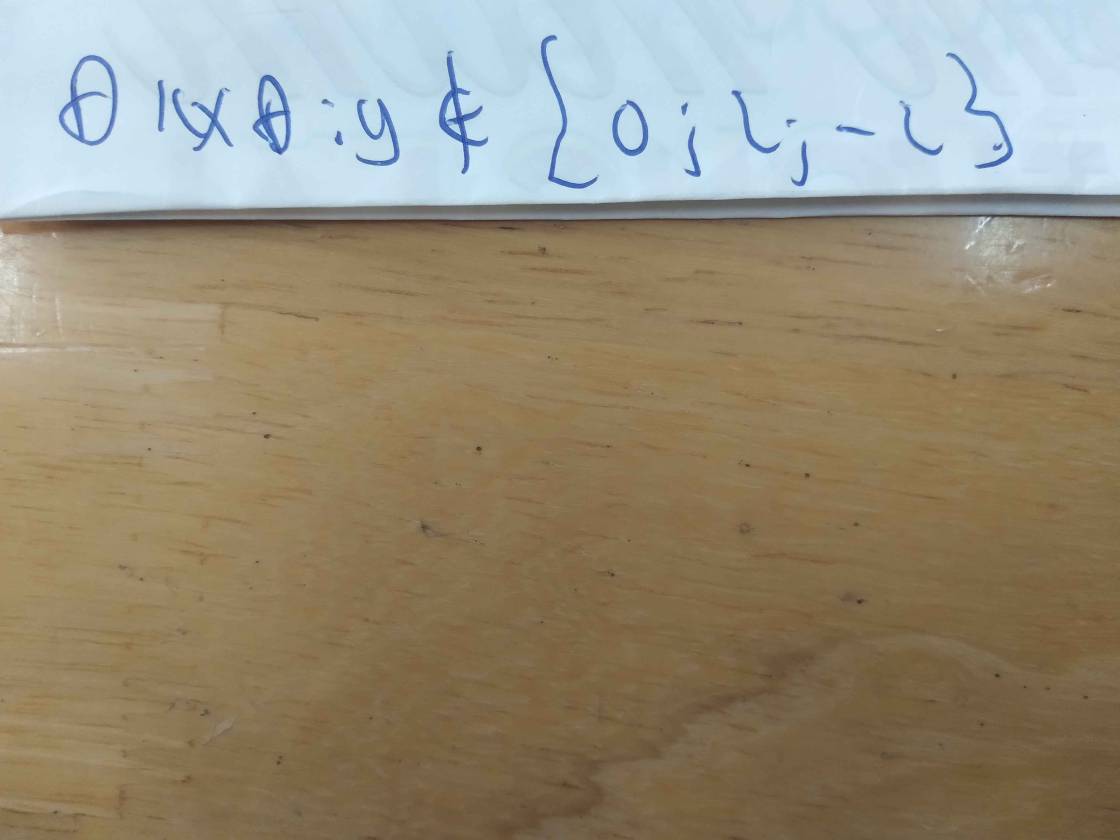



Gọi độ dài quãng đường từ Hà Giang đến Hà Nội là x(km)
(ĐK: x>0)
Thời gian đi từ Hà Giang đến Hà Nội là \(\dfrac{x}{60}\left(giờ\right)\)
Thời gian đi từ Hà Nội về Hà Giang là \(\dfrac{x}{50}\left(giờ\right)\)
Thời gian đi ít hơn thời gian về là 1 giờ nên ta có: \(\dfrac{x}{50}-\dfrac{x}{60}=1\)
=>\(\dfrac{x}{300}=1\)
=>x=300(nhận)
Vậy: độ dài quãng đường từ Hà Giang đến Hà Nội là 300km