1+1+978978+564561+456786+4+564+56+4+5+6+5+6+7+86++789+7+9+78+97+89+78+97+89+78+9+789+7+89+75+6+4+5+3+42+1+32+1++321+2+21+31+23+1+23+123+12+3+123+132++13+13+2+12+13+2+132+312+312+2+31+3=?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


"BSĐ: tìm nghiệm nguyên"
`x+2y+xy=5`
`=>x+y(x+2)=5`
`=>(x+2)+y(x+2)=5+2`
`=>(x+2)(y+1)=7`
Ta có bảng:
| x + 2 | 1 | 7 | -1 | -7 |
| y + 1 | 7 | 1 | -7 | -1 |
| x | -1 | 5 | -3 | -9 |
| y | 6 | 0 | -8 | -2 |
Vậy: ..
nếu (x=1):[1+2y+1/cdot y=5] [1+2y+y=5] [1+3y=5] [3y=4] [y=\frac{4}{3}]
Vậy là (x=1) và (y=\frac{4}{3})
bạn xem có đúng ko nhé

`1)` Ta có:
`Ư(15)={1;3;5;15}`
`Ư(20)={1;2;4;5;10;20}`
`=>ƯC(15;20)={1;5}`
`2)` Ta có:
`18=3^2*2`
`60=2^2*3*5`
`=>ƯCLN(18;60)=3*2=6`
`3)` Ta có:
`9=3^2`
`14=2*7`
`=>ƯCLN(9;14)=1`
`4)ƯCLN(4;10)=2`
`5)` 3 ⋮ n + 1
=> n + 1 ∈ Ư(3) = {1; -1; 3; -3}
Mà n là số tự nhiên => `n+1>=1`
=> n + 1 ∈ {1; 3}
=> n ∈ {0; 2}

\(2a-b=\dfrac{2}{3}\left(a+b\right)\)
\(3\left(2a-b\right)=2\left(a+b\right)\)
\(6a-3b=2a+2b\)
\(4a=5b\)
\(a=\dfrac{5}{4}b\)
Thay vào A ta được:
\(A=\dfrac{\left(\dfrac{5}{4}b\right)^4+5^4}{b^4+4^4}=\dfrac{\dfrac{5^4}{4^4}\left(b^4+4^4\right)}{b^4+4}=\dfrac{5^4}{4^4}\)

a.
\(\left(2x-3\right)^2=400\)
\(\left(2x-3\right)^2=20^2\)
\(2x-3=20\) hoặc \(2x-3=-20\)
\(2x=23\) hoặc \(2x=-17\)
\(x=\dfrac{23}{2}\notin N\) hoặc \(x=-\dfrac{17}{2}\notin N\)
Vậy không có số tự nhiên x thỏa mãn
b.
\(5^{x+4}-3.5^{x+3}=2.5^{11}\)
\(5^{x+3}\left(5-3\right)=2.5^{11}\)
\(2.5^{x+3}=2.5^{11}\)
\(5^{x+3}=5^{11}\)
\(x+3=11\)
\(x=8\)
c.
\(5.3^{x+6}=2.3^5+3.3^5\)
\(5.3^{x+6}=3^5\left(2+3\right)\)
\(5.3^{x+6}=2.3^5\)
\(3^{x+6}=3^5\)
\(x+6=5\)
\(x=-1\notin N\)
Vậy ko có số tự nhiên x thỏa mãn
`(2x - 3)^2 = 400`
`<=> (2x - 3)^2 = 20^2`
`<=> 2x - 3 = -20` hoặc `2x - 3 = 20`
`<=> 2x = -17` hoặc `2x = 23`
`<=> x = -17/2` hoặc `x = 23/2` (ko thỏa mãn)
Vậy ...
`5^(x+4) - 3 . 5^(x+3) = 2 . 5^11`
`<=> 5^(x+3) . 5 - 3 . 5^(x+3) = 2 . 5^11`
`<=> 5^(x+3) . (5 - 3) = 2 . 5^11`
`<=> 5^(x+3) . 2 = 2 . 5^11`
`<=> x + 3 = 11`
`<=> x = 8`
Vậy ...
`5 . 3^(x+6) = 2.3^5 + 3 . 3^5 `
`<=>5 . 3^(x+6) = (2+ 3) . 3^5 `
`<=>5 . 3^(x+6) = 5 . 3^5 `
`<=> x + 6 = 5`
`<=> x = -1 ` (không thỏa mãn)
Vậy ...

\(=8^{6-4}+3^3-1+2^{20+10}-2^{30}\)
\(=8^2+3^3-1+2^{30}-2^{30}\)
\(=8^2+3^3-1\)
\(=64+27-1\)
\(=90\)

Số đường còn lại sau buổi sáng là:
`180 - 60 = 120 (kg) `
Số đường bán đi trong buổi chiều là:
`120 xx 2/5 = 48 (kg)`
Số đường còn lại là:
`12 0- 48 = 72 (kg)`
Đáp số: ...

\(\dfrac{x+8}{28}+\dfrac{x+10}{27}=\dfrac{x+12}{26}+\dfrac{x+14}{25}\)
\(\left(\dfrac{x+8}{28}+2\right)+\left(\dfrac{x+10}{27}+2\right)=\left(\dfrac{x+12}{26}+2\right)+\left(\dfrac{x+14}{25}+2\right)\)
\(\dfrac{x+64}{28}+\dfrac{x+64}{27}=\dfrac{x+64}{26}+\dfrac{x+64}{25}\)
\(\dfrac{x+64}{28}+\dfrac{x+64}{27}-\dfrac{x+64}{26}-\dfrac{x+64}{25}=0\)
\(\left(x+64\right)\left(\dfrac{1}{28}+\dfrac{1}{27}-\dfrac{1}{26}-\dfrac{1}{25}\right)=0\)
\(x+64=0\) (do \(\dfrac{1}{28}+\dfrac{1}{27}-\dfrac{1}{26}-\dfrac{1}{25}\ne0\))
\(x=-64\)

\(10M=\dfrac{10.\left(10^{100}+1\right)}{10^{101}+1}=\dfrac{10^{101}+10}{10^{101}+1}=\dfrac{10^{101}+1+9}{10^{101}+1}=1+\dfrac{9}{10^{101}+1}\)
\(10N=\dfrac{10.\left(10^{101}+1\right)}{10^{102}+1}=\dfrac{10^{102}+10}{10^{102}+1}=\dfrac{10^{102}+1+9}{10^{102}+1}=1+\dfrac{9}{10^{102}+1}\)
Do \(10^{101}< 10^{102}\Rightarrow10^{101}+1< 10^{102}+1\)
\(\Rightarrow\dfrac{9}{10^{101}+1}>\dfrac{9}{10^{102}+1}\)
\(\Rightarrow1+\dfrac{9}{10^{101}+1}>1+\dfrac{9}{10^{102}+1}\)
\(\Rightarrow10M>10N\)
\(\Rightarrow M>N\)

\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{3}\)
\(\dfrac{x+y}{xy}=\dfrac{1}{3}\)
\(3\left(x+y\right)=xy\)
\(xy-3x-3y=0\)
\(xy-3x-3y+9=9\)
\(x\left(y-3\right)-3\left(y-3\right)=9\)
\(\left(x-3\right)\left(y-3\right)=9\)
Ta có bảng sau:
| x-3 | -9 | -3 | -1 | 1 | 3 | 9 |
| y-3 | -1 | -3 | -9 | 9 | 3 | 1 |
| x | -6 | 0 (loại) | 2 | 4 | 6 | 12 |
| y | 2 | 0 (loại) | -6 | 12 | 6 | 4 |
Vậy \(\left(x;y\right)=\left(-6;2\right);\left(2;-6\right);\left(4;12\right);\left(6;6\right);\left(12;4\right)\)
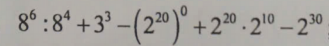
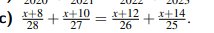
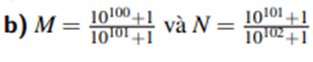
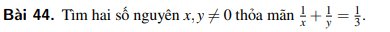
????