a)Ta có:

AB = AC ( tam giác ABC cân tại A )

=> 1/2 AB = 1/2 AC hay AE = AD

Xét ΔABD và ΔACE có:

AB = AC(cmt)

góc A chung

AD = AE (cmt)

=> 2Δ bằng nhau

=> BD=CE

b) BD = CE ( cmt )

=> 2/3 BD = 2/3 CE hay GB = GC

=> ΔGBC cân tại G

c) GD+GE = 1/3CD = 1/3CE

Mà BD = CE (cmt)

=> 1/3 BD + 1/3 CE = 2/3 BD = BG

Gọi F là t/đ BC 

=> BF = 1/2 BC

Xét tg BGF vuông tại F ( do tg ABC cân => AF vuông góc Bc ):

BG>BF(ch>cgv)

=> GD + GE> 1/2BC

a,�,

Do CE�� là đường trung tuyến (gt)

→E→� là trung điểm của AB��

Do BD�� là đường trung tuyến (gt)

→D→� là trung điểm của AC��

Có : AE=12AB��=12�� (Do E� là trung điểm của AB��)

Có : AD=12AC��=12�� (Do D� là trung điểm của AC��)

mà AB=AC��=�� (Do ΔABCΔ��� cân tại A�) →12AB=12AC→12��=12��

→AE=AD

Xét ΔADBΔ��� và ΔAECΔ��� có :

AE=AD��=�� (cmt)

AB=AC��=�� (Do ΔABCΔ��� cân tại A�)

ˆA�^ chung

→ΔADB=ΔAEC→Δ���=Δ��� (cạnh - góc - cạnh)

→BD=CE→��=�� (2 cạnh tương ứng)

và ˆABD=ˆACE���^=���^ (2 góc tương ứng)

Có : ˆABD+ˆGBC=ˆABC���^+���^=���^

Có : ˆACE+ˆGCB=ˆACB���^+���^=���^

mà ˆABD=ˆACE���^=���^ (cmt), ˆABC=ˆACB���^=���^ (Do ΔABCΔ��� cân tại A�)

→ˆGBC=ˆGCB→���^=���^

→ΔBGC→Δ��� cân tại G�

Vì G là trọng tâm tam giác ABC nên:

GD=12GB,GE=12GC��=12��,��=12��

Do đó GD+GE=12BG+12CG=12(BG+CG)��+��=12��+12��=12��+��.

Mặt khác: BG + CG > BC (bất đẳng thức trong tam giác GCB).

Suy ra GB+GE>12BC��+��>12�� (điều phải chứng minh).

dễ ấy mà

\(a,x^2-2=0\Leftrightarrow x^2-\left(\sqrt{2}\right)^2=0\Leftrightarrow\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)

Vậy \(S=\left\{-\sqrt{2};\sqrt{2}\right\}\)

\(b,x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

Vậy \(S=\left\{0;2\right\}\)

\(c,x^2-2x=0\Leftrightarrow x\left(x-2\right)\) phương trình như câu b, 

\(d,x\left(x^2+1\right)\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=-1\left(voli\right)\end{matrix}\right.\)( voli là vô lí )

Vậy \(S=\left\{0\right\}\)

a,x2−2=0⇔x2−(2​)2=0⇔(x−2​)(x+2​)=0⇔[x=2​x=−2​​

Vậy �={−2;2}S={−2​;2​}

�,�(�−2)=0⇔[�=0�=2b,x(x−2)=0⇔[x=0x=2​

Vậy �={0;2}S={0;2}

�,�2−2�=0⇔�(�−2)c,x2−2x=0⇔x(x−2) phương trình như câu b, 

�,�(�2+1)⇔[�=0�2+1=0⇔[�=0�2=−1(����)d,x(x2+1)⇔[x=0x2+1=0​⇔[x=0x2=−1(voli)​( voli là vô lí )

Vậy �={0}S={0}

Ta có:
\(\dfrac{x}{10}=\dfrac{y}{5}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}\)  \(\left(1\right)\)
\(\dfrac{y}{2}=\dfrac{z}{3}\)
\(\Rightarrow\dfrac{y}{10}=\dfrac{z}{15}\)  \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
Lại có:
\(\dfrac{z}{15}=\dfrac{4z}{60}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{4z}{60}=\dfrac{x+4z}{20+60}=\dfrac{240}{80}=3\)
\(\Rightarrow x=3\cdot20=60\)
     \(y=3\cdot10=30\)
     \(z=3\cdot15=45\)

H(-1) = 2\(x^2\)- 10 

H(-1) = 2.(-1)² - 10

H(-1) = 2 - 10

H(-1) = -8

H(\(\dfrac{1}{2}\)) = 2\(x^2\) - 10

H(\(\dfrac{1}{2}\)) = 2.(\(\dfrac{1}{2}\))² - 10

H(\(\dfrac{1}{2}\)) = \(\dfrac{1}{2}\) - 10

H(\(\dfrac{1}{2}\)) = \(-\dfrac{19}{2}\)

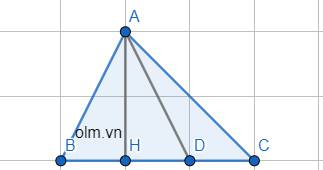
Vì AH \(\perp\) BC  \(\equiv\) H  nên:

BH là hình chiếu của AB trên BC

HC là hình chiếu của AC trên BC

AB < AC => BH < HC ( Mối quan hệ đường xiên và hình chiếu )

\(\widehat{BAH}\) Đối diện cạnh BH

\(\widehat{HAC}\) Đối diện cạnh HC

mà BH < HC ( chứng minh trên)

=> \(\widehat{BAH}\) < \(\widehat{HAC}\) ( mối quan hệ giữa cạnh và góc trong tam giác)

Ta có : HD = HB (gt) (1)

            AH \(\perp\) BD \(\equiv\) H (2)

Từ (1) và (2) ta có : \(\Delta\) ABD cân tại A vì AH vừa là đường cao vừa là đường trung tuyến của \(\Delta\) ABD

mn giúp mk với ạ!

a) G = {hs đến từ nước Mỹ , hs đến từ Anh , hs đến từ Pháp , hs đến từ Thái Lan , hs đến từ Việt Nam , hs đến từ Canada, hs đến từ Thụy Sĩ , hs đến từ Nga , hs đến từ Brasil

b) 

- kết quả có thể xảy ra : có 9 kết quả

- kết quả thuận lợi cho biến cố * Học sinh đến từ châu Á* : hs đến từ Thái , hs đến từ Việt => có 2 kq

- xác xuất của biến cố : 2/9

a) Tập hợp các kết quả có thể xảy ra đối với học sinh được chọn ra là:

�={G={Mỹ; Anh; Pháp; Thái Lan; Việt Nam; Canada; Thụy Sĩ; Nga; Brasil}}.

Số phần tử của tập hợp G là 9.

b) Trong 9 nước trên có các nước thuộc châu Á là: Việt Nam và Thái Lan.9

Do đó có 2 kết quả thuận lợi cho biến cố "Học sinh được chọn ra đến từ châu Á" là: Việt Nam; Thái Lan.

Khi đó xác suất của biến cố "Học sinh được chọn ra đến từ châu Á" bằng: 2/9.