
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(-\dfrac{3}{2}x\right)^2\cdot\left(-4\right)x^3\)
\(=\dfrac{9}{4}x^2\cdot\left(-4\right)x^3\)
\(=\left[\dfrac{9}{4}\cdot\left(-4\right)\right]\cdot\left(x^2\cdot x^3\right)\)
\(=-9x^5\)
\(\rightarrow\) Đơn thức A có bậc là 5
A = (-3/2 x)² .(-4x³)
= 9/4 x² . (-4x³)
= -9x⁵
Bậc của đơn thức A là 5

a) Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E, ta có:
BD là cạnh chung
góc ABD = góc DBE ( Vì BD là tia phân giác góc ABC )
`=>` tam giác ABD = tam giác EBD ( ch.gn )
b) Xét tam giác BAC và tam giác BEF, ta có:
góc FBC chung
BA = BE ( Vì tam giác ABD = tam giác EBD )
góc BAC = góc BEF = 90 độ
`=>` tam giác BAC = tam giác BEF ( g.c.g )
`=>` BF = BC ( 2 cạnh tương ứng )
`#NqHahh`
@linh nguyen
Bạn vô trang cá nhân của mình xem hình vẽ nhé.

Do x và y là hai đại lượng tỉ lệ nghịch
\(\Rightarrow\dfrac{y_1}{y_2}=\dfrac{x_2}{x_1}\)
Do \(\dfrac{y_1}{y_2}=-1\Rightarrow\dfrac{x_2}{x_1}=-1\)
\(\Rightarrow x_1=-x_2;y_2=-y_1\)
\(\Rightarrow x_1-y_2=-x_2-\left(-y_1\right)=y_1-x_2=-18\)
Do x;y là 2 đại lượng tỉ lệ nghịch
\(\Rightarrow x_1y_1=x_2y_2\Rightarrow\dfrac{y_1}{y_2}=\dfrac{x_2}{x_1}=\dfrac{y_1-x_2}{y_2-x_1}=-1\)
\(\Rightarrow\dfrac{-18}{y_2-x_1}=-1\Rightarrow y_2-x_1=18\)
\(\Rightarrow x_1-y_2=-18\)

\(x\) tỉ lệ thuận với \(y\) theo hệ số tỉ lệ là 2
\(\Rightarrow x=2y\)
\(y\) tỉ lệ thuận với \(z\) theo hệ số tỉ lệ \(-\dfrac{1}{2}\)
\(\Rightarrow y=\dfrac{-1}{2}.z\)
\(\Rightarrow x=2y=2.\left(-\dfrac{1}{2}.z\right)=-z\)
Khi \(x=5\Rightarrow-z=5\Rightarrow z=-5\)
x tỉ lệ thuận y theo hệ số tỉ lệ \(k=2\Rightarrow x=2y\)
y và z tỉ lệ nghịch theo hệ số tỉ lệ \(k=-\dfrac{1}{2}\Rightarrow yz=-\dfrac{1}{2}\)
Khi \(x=-5\Rightarrow y=\dfrac{x}{2}=-\dfrac{5}{2}\)
\(\Rightarrow\left(-\dfrac{5}{2}\right).z=-\dfrac{1}{2}\)
\(\Rightarrow z=-\dfrac{1}{2}:\left(-\dfrac{5}{2}\right)=\dfrac{1}{5}\)

\(2x\left(3x^2+4x+1\right)\)
\(=2x.3x^2+2x.4x+2x.1\)
\(=6x^3+8x^2+2x\)
------------------
\(\left(2x+1\right)\left(x-2\right)\)
\(=2x\left(x-2\right)+1.\left(x-2\right)\)
\(=2x.x-2x.2+x-2\)
\(=2x^2-4x+x-2\)
\(=2x^2+\left(-4x+x\right)-2\)
\(=2x^2-3x-2\)

a, Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến.
P(\(x\)) = 7\(x^3\) + 4\(x^4\) - 2\(x^2\) + 3\(x^2\) - 3\(x^3\) - \(x^4\) + 5 - 4\(x^3\)
P(\(x\)) = (7\(x^3\) - 3\(x^3\) - 4\(x^3\))+ (4\(x^4\) - \(x^4\)) - (2\(x^2\) - 3\(x^2\)) + 5
P(\(x\)) = 0 + 3\(x^4\) - (-\(x^2\)) +5
P(\(x\)) = 3\(x^4\) + \(x^2\) + 5
b; Hệ số cao nhất là 3; bậc của đa thức là 4; hệ số tự do của đa thức trên là 5

Olm chào em, hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp thế như sau:
Giải:
\(\dfrac{x}{y}\) = \(\dfrac{3}{-2}\) và \(x-y\) = 2y
\(x\) - y = 2y ⇒ \(x\) = 2y + y ⇒ \(x\) = 3y
Thay \(x=3y\) vào biểu thức \(\dfrac{x}{y}\) = \(\dfrac{3}{-2}\) ta có: \(\dfrac{3y}{y}\) = \(\dfrac{3}{-2}\)
⇒ 3 = \(\dfrac{3}{-2}\) (vô lí)
Vậy không có giá trị nào của \(x;y\) thỏa mãn đề bài.
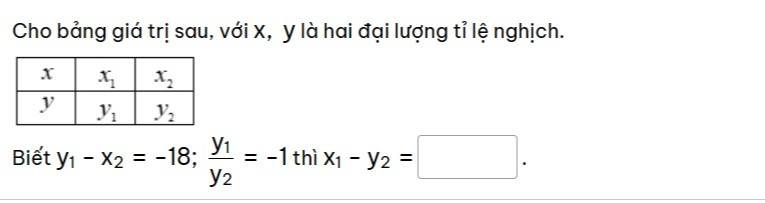
a: Xét ΔMHN vuông tại H và ΔMHP vuông tại H có
MN=MP
MH chung
Do đó: ΔMHN=ΔMHP
b: Ta có: EF//MP
=>\(\widehat{EFN}=\widehat{MPN}\)
=>\(\widehat{EFN}=\widehat{ENF}\)
=>ΔENF cân tại E
=>EN=EF
c: Ta có: EF=EN
mà EN=PI
nên EF=PI
Xét ΔMEF và ΔMIP có
\(\widehat{MFE}=\widehat{MPI}\)(FE//PI)
EF=PI
\(\widehat{MEF}=\widehat{MIP}\)(EF//IP)
Do đó: ΔMEF=ΔMIP
=>ME=MI
=>M là trung điểm của EI