Cho tứ giác ABCD. Gọi M, N, H lần lượt là trung điểm của AD, BC, AC. a) Chứng minh MN // CD; NH // AB. 1 b) So sánh MN và (AB + CD).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC có EI//BC
nên \(\dfrac{AE}{AB}=\dfrac{AI}{AC}\left(1\right)\)
Xét ΔADC có FI//DC
nên \(\dfrac{AI}{AC}=\dfrac{AF}{AD}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AE}{AB}=\dfrac{AF}{AD}\)
Xét ΔABD có \(\dfrac{AE}{AB}=\dfrac{AF}{AD}\)
nên EF//BD
b: Xét ΔCBA có GI//AB
nên \(\dfrac{CG}{BG}=\dfrac{CI}{IA}\left(3\right)\)
Xét ΔCAD có IH//AD
nên \(\dfrac{CI}{IA}=\dfrac{CH}{HD}\left(4\right)\)
Từ (3),(4) suy ra \(\dfrac{CG}{BG}=\dfrac{CH}{HD}\)
=>\(CG\cdot HD=BG\cdot CH\)


a: Ta có: AK=KO=OH
=>\(AK=KO=OH=\dfrac{1}{3}AH\)
=>\(AO=\dfrac{2}{3}AH;AK=\dfrac{1}{3}AH\)
Xét ΔAHB có EK//BH
nên \(\dfrac{AE}{AB}=\dfrac{AK}{AH}\)
=>\(\dfrac{AE}{AB}=\dfrac{1}{3}\)
Xét ΔABH có MO//BH
nên \(\dfrac{AM}{AB}=\dfrac{AO}{AH}\)
=>\(\dfrac{AM}{AB}=\dfrac{2}{3}\)
Xét ΔABC có EF//BC
nên \(\dfrac{EF}{BC}=\dfrac{AE}{AB}\)
=>\(\dfrac{EF}{BC}=\dfrac{1}{3}\)
=>\(EF=\dfrac{BC}{3}=\dfrac{30}{3}=10\left(cm\right)\)
Xét ΔABC có MP//BC
nên \(\dfrac{MP}{BC}=\dfrac{AM}{AB}\)
=>\(\dfrac{MP}{30}=\dfrac{2}{3}\)
=>\(MP=20\left(cm\right)\)
b: Xét ΔAMP và ΔABC có
\(\widehat{AMP}=\widehat{ABC}\)(hai góc đồng vị, MP//BC)
\(\widehat{MAP}\) chung
Do đó: ΔAMP~ΔABC
=>\(\dfrac{S_{AMP}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2\)
=>\(\dfrac{S_{AMP}}{10.8}=\dfrac{4}{9}\)
=>\(S_{AMP}=4,8\left(dm^2\right)\)
Xét ΔAEF và ΔABC có
\(\widehat{AEF}=\widehat{ABC}\)(hai góc đồng vị, EF//BC)
\(\widehat{FAE}\) chung
Do đó: ΔAEF~ΔABC
=>\(\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=\dfrac{1}{9}\)
=>\(S_{AEF}=\dfrac{10.8}{9}=1,2\left(dm^2\right)\)
Ta có: \(S_{AEF}+S_{MEFP}=S_{AMP}\)
=>\(S_{MEFP}+1,2=4,8\)
=>\(S_{MEFP}=3,6\left(dm^2\right)\)

\(A=\dfrac{2}{6x-5-9x^2}\)
\(=\dfrac{2}{-9x^2+6x-5}\)
\(=\dfrac{2}{-\left(9x^2-6x+5\right)}\)
\(=\dfrac{2}{-\left(9x^2-6x+1+4\right)}\)
\(=\dfrac{2}{-\left(3x-1\right)^2-4}\)
\(\left(3x-1\right)^2>=0\forall x\)
=>\(-\left(3x-1\right)^2< =0\forall x\)
=>\(-\left(3x-1\right)^2-4< =-4\forall x\)
=>\(A=\dfrac{2}{-\left(3x-1\right)^2-4}>=\dfrac{2}{-4}=-\dfrac{1}{2}\forall x\)
Dấu '=' xảy ra khi 3x-1=0
=>3x=1
=>\(x=\dfrac{1}{3}\)

a: Xét ΔAEH vuông tại E và ΔAHC vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHC
b: Ta có: ΔAEH vuông tại E
=>\(EH^2+EA^2=AH^2\)
=>\(EH^2=10^2-6^2=64=8^2\)
=>EH=8(cm)
Xét ΔAHE có AM là phân giác
nên \(\dfrac{MH}{AH}=\dfrac{ME}{AE}\)
=>\(\dfrac{MH}{10}=\dfrac{ME}{6}\)
=>\(\dfrac{MH}{5}=\dfrac{ME}{3}\)
mà MH+ME=EH=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MH}{5}=\dfrac{ME}{3}=\dfrac{MH+ME}{5+3}=\dfrac{8}{8}=1\)
=>MH=5(cm); ME=3(cm)
c: Xét ΔHEC có HN là phân giác
nên \(\dfrac{EN}{NC}=\dfrac{EH}{HC}\left(1\right)\)
Xét ΔAHE có AM là phân giác
nên \(\dfrac{EM}{MH}=\dfrac{EA}{AH}\left(2\right)\)
Xét ΔEHA vuông tại E và ΔHCA vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔEHA~ΔHCA
=>\(\dfrac{EA}{HA}=\dfrac{EH}{HC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{EM}{MH}=\dfrac{EN}{NC}\)
Xét ΔEHC có \(\dfrac{EM}{MH}=\dfrac{EN}{NC}\)
nên MN//HC
=>MN//BC
mà AH\(\perp\)BC
nên HA\(\perp\)MN
Xét ΔAHN có
NM,HE là các đường cao
NM cắt HE tại M
Do đó: M là trực tâm của ΔAHN
=>AM\(\perp\)HN

Gọi số tự nhiên ban đầu là X
Viết thêm chữ số 2 vào bên trái và một chữ số 2 vào bên phải thì số mới sẽ là 10X+2000+2=10X+2002
Số mới gấp 153 lần số ban đầu nên ta có:
10X+2002=153X
=>143X=2002
=>\(X=\dfrac{2002}{143}=14\left(nhận\right)\)
Vậy: Số cần tìm là 14

Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian dự kiến ban đầu là \(\dfrac{x}{40}\left(giờ\right)\)
Thời gian đi nửa quãng đường ban đầu là \(\dfrac{x}{2}:40=\dfrac{x}{80}\left(giờ\right)\)
vận tốc trên nửa quãng đường còn lại là 40+10=50(km/h)
Thời gian đi nửa quãng đường còn lại là \(\dfrac{x}{2}:50=\dfrac{x}{100}\left(giờ\right)\)
Tổng thời gian là 11h30p-6h30p-30p=4h30p=4,5(giờ)
Theo đề, ta có phương trình:
\(\dfrac{x}{80}+\dfrac{x}{100}=4,5\)
=>\(\dfrac{9x}{400}=4,5\)
=>\(9x=400\cdot4,5=1800\)
=>\(x=\dfrac{1800}{9}=200\left(nhận\right)\)
vậy: Quãng đường AB là 200km

a: \(P=\dfrac{x}{x-2}+\dfrac{2-x}{x+2}+\dfrac{8-6x}{x^2-4}\)
\(=\dfrac{x}{x-2}-\dfrac{x-2}{x+2}+\dfrac{8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x+2\right)-\left(x-2\right)^2+8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x-x^2+4x-4+8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{x^2-4}\)
b: Thay x=3 vào P, ta được:
\(P=\dfrac{4}{3^2-4}=\dfrac{4}{5}\)
Thay x=-1/2 vào P, ta được:
\(P=\dfrac{4}{\left(-\dfrac{1}{2}\right)^2-4}=\dfrac{4}{\dfrac{1}{4}-4}=4:\dfrac{-15}{4}=\dfrac{-16}{15}\)
c: Để P là số nguyên thì \(4⋮x^2-4\)
=>\(x^2-4\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x^2\in\left\{5;3;6;2;8;0\right\}\)
mà x nguyên
nên x^2=0
=>x=0(nhận)

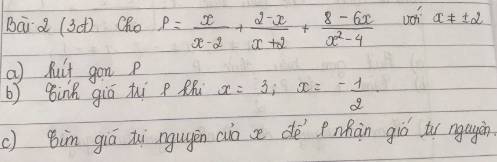
a: Sửa đề: MH//CD
Xét ΔADC có
M,H lần lượt là trung điểm của AD,AC
=>MH là đường trung bình của ΔADC
=>MH//DC và \(MH=\dfrac{DC}{2}\)
Xét ΔCABcó
N,H lần lượt là trung điểm của CB,CA
=>NH là đường trung bình của ΔCAB
=>NH//AB và \(NH=\dfrac{AB}{2}\)
b: MH+HN<=MN
=>\(\dfrac{1}{2}\left(AB+CD\right)< =MN\)
=>\(MN>=\dfrac{1}{2}\left(AB+CD\right)\)