`=30+30*0+1`

`=30+0+1`

`=31`

31

Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$Q=|x-2020|+|x-2021|=|x-2020|+|2021-x|\geq |x-2020+2021-x|=1$
Vậy $Q_{\min}=1$
Giá trị này đạt tại $(x-2020)(2021-x)\geq 0$

$\Leftrightarrow 2020\leq x\leq 2021$

$x\in\mathbb{N}$ nên $x\in\left\{2020; 2021\right\}$

Đề không có yêu cầu. Bạn coi lại đề.

100 m2 100m2 100m2

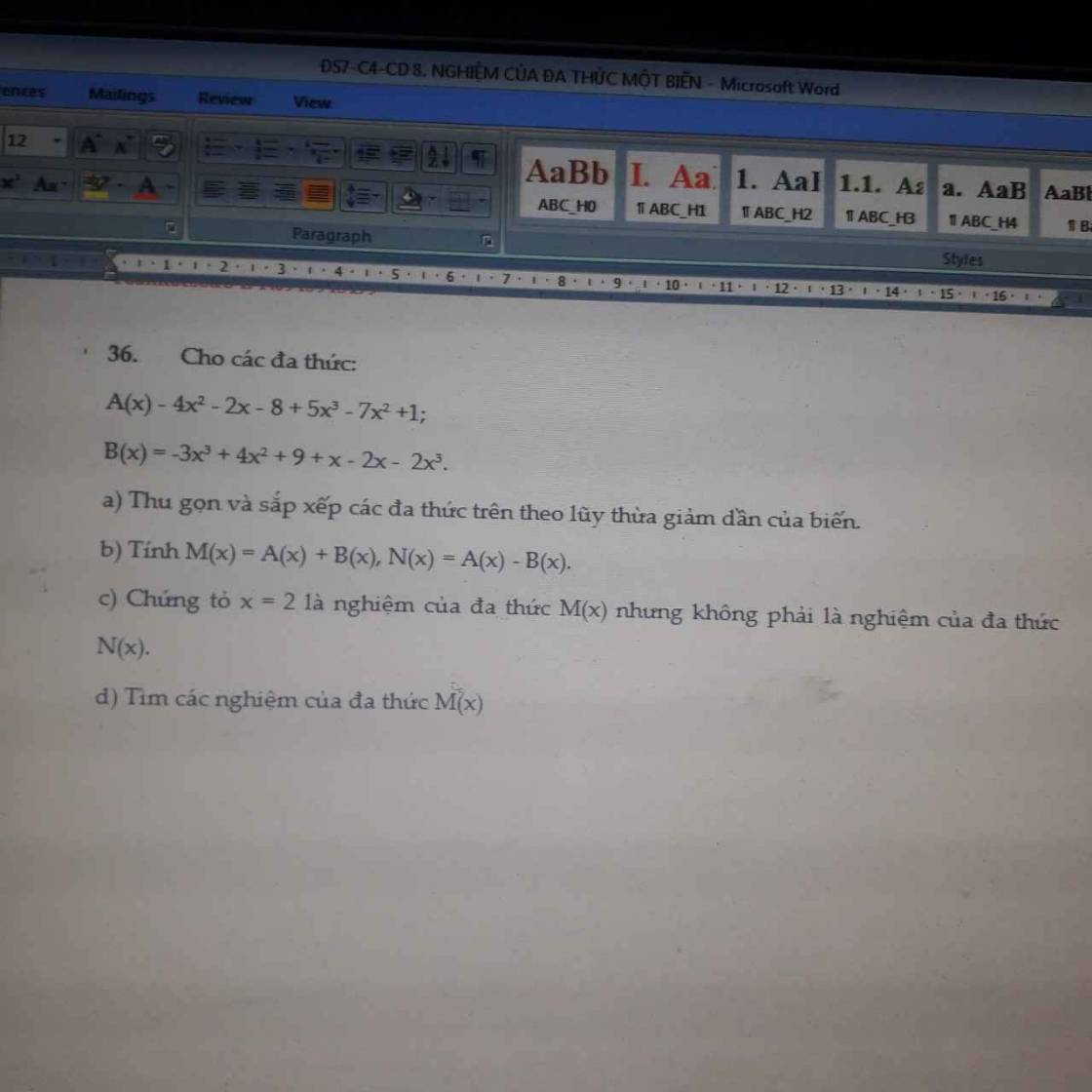
a)

\(A\left(x\right)=4x^2-2x-8+5x^3-7x^2+1\\ \text{ }=5x^3-\left(7x^2-4x^2\right)-2x-\left(8-1\right)\\ \text{ }=5x^3-3x^2-2x-7\)

\(B\left(x\right)=-3x^3+4x^2+9+x-2x-2x^3\\ \text{ }=\left(-3x^3-2x^3\right)+4x^2+\left(x-2x\right)+9\\ \text{ }=-5x^3+4x^2-x+9\)

b)

\(M\left(x\right)=A\left(x\right)+B\left(x\right)\\ \text{ }=\left(5x^3-3x^2-2x-7\right)+\left(-5x^3+4x^2-x+9\right)\\ \text{ }=5x^3-3x^2-2x-7-5x^3+4x^2-x+9\\ \text{ }=\left(5x^3-5x^3\right)+\left(4x^2-3x^2\right)-\left(2x-x\right)+\left(9-7\right)\\ \text{ }=x^2-x+2\)

\(N\left(x\right)=A\left(x\right)-B\left(x\right)\\ \text{ }=\left(5x^3-3x^2-2x-7\right)-\left(-5x^3+4x^2-x+9\right)\\ \text{ }=5x^3-3x^2-2x-7+5x^3-4x^2+x-9\\ \text{ }=\left(5x^3+5x^3\right)-\left(3x^2+4x^2\right)-\left(2x-x\right)-\left(7+9\right)\\ \text{ }=10x^3-7x^2-x-16\)

Thầy cô và các bạn giúp mình với ạ

Lời giải:

Ta có:
$f(1)=a+b+c$
$f(-2)=4a-2b+c$

$\Rightarrow 2f(-2)+3f(1)=2(4a-2b+c)+3(a+b+c)=11a-b+5c=0$

$\Rightarrow f(-2)=\frac{-3}{2}f(1)$

Vì $\frac{-3}{2}<0$ nên $f(-2)$ và $f(1)$ không thể cùng dấu.

r u ok

`P(x)=2x^5+2x+8-3x^2-2x^5+2x^3-4x^4 `

`= (2x^5 -2x^5) -4x^4 +2x^3 -3x^2 +2x +8`

`= -4x^4 +2x^3 -3x^2 +2x +8`

Bậc của `P(x)=10`

sai chỗ nào :))

có lộn đề không ạ