cho tam giác abc có 3 góc nhọn ab<ac, kẻ đường cao be và cf cắt nhau tại h
a) chứng minh tam giác aeb đồng dạng với tam giác afc
b)góc aef = góc abc
c) tam giác hef đồng dạng với tam giác hcb
d) lấy điểm k sao cho bc là đường trung trực của kh. gọi m,n lần lượt là hình chiếu của k trên ab, ac c/m: tam giác kmb đồng dạng với tam giác knc và mn đi qua trung điểm của kh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: \(x^2-11x-12=0\)
=>\(x^2-12x+x-12=0\)
=>(x-12)(x+1)=0
=>\(\left[{}\begin{matrix}x=12\\x=-1\end{matrix}\right.\)

Chúng ta sẽ chia ra 2 loại:
Loại 1: ba đỉnh ko có điểm A, loại 2: ba đỉnh có điểm A
Loại 1: ba đỉnh không có điểm A
TH1: 2 điểm nằm trên tia Ax, 1 điểm nằm trên tia Ay
Số cách lấy 2 điểm nằm trên tia Ax(không phải điểm A) là:
\(C^2_6\left(cách\right)\)
Số cách lấy 1 điểm nằm trên tia Ay(không phải điểm A) là 5 cách
Do đó: Có \(C^2_6\cdot5\left(cách\right)\)
TH2: 2 điểm nằm trên tia Ay, 1 điểm nằm trên tia Ax
Số cách lấy 1 điểm nằm trên tia Ax(không phải điểm A) là: 6(cách)
Số cách lấy 2 điểm nằm trên tia Ay(không phải điểm A) là:
\(C^2_5\left(cách\right)\)
=>Có \(6\cdot C^2_5\left(cách\right)\)
Tổng số cách là \(5\cdot C^2_6+6\cdot C^2_5=135\left(cách\right)\)
Loại 2: ba đỉnh có điểm A
Số cách lấy 1 điểm nằm trên tia Ax là 6(cách)
Số cách lấy 1 điểm nằm trên tia Ay là 5(cách)
Do đó: Có \(6\cdot5=30\left(cách\right)\)
Tổng số cách của cả 2 loại là 135+30=165(cách)

Lời giải:
Đặt $\frac{n(n+1)(n+2)}{6}+1=p$ với $p$ là snt
$\Leftrightarrow n(n+1)(n+2)+6=6p$
$\Leftrightarrow (n+3)(n^2+2)=6p$
Do $n+3\geq 3; n^2+2\geq 2$ với mọi $n$ tự nhiên nên ta có các TH sau:
TH1: $n+3=3, n^2+2=2p\Rightarrow n=0; p=1$ (loại)
TH2: $n+3=6, n^2+2=p\Rightarrow n=3; p=11$ (tm)
TH3: $n+3=p, n^2+2=6\Rightarrow n=2; p=5$ (tm)
TH4: $n+3=2p; n^2+2=3\Rightarrow n=1; p=2$ (tm)
TH5: $n+3=3p; n^2+2=2\Rightarrow n=0; p=1$ (loại)

\(11x+42-2x=100-9x-22\\ 11x-2x+9x=100-22-42\\ 18x=36\\ x=\dfrac{36}{18}=2\)

1: Xét ΔADH vuông tại D và ΔAHB vuông tại H có
\(\widehat{DAH}\) chung
Do đó: ΔADH~ΔAHB
2: Xét ΔEHA vuông tại E và ΔECH vuông tại E có
\(\widehat{EHA}=\widehat{ECH}\left(=90^0-\widehat{EHC}\right)\)
Do đó: ΔEHA~ΔECH
=>\(\dfrac{EH}{EC}=\dfrac{EA}{EH}\)
=>\(EH^2=EA\cdot EC\)
3: Xét ΔAEH vuông tại E và ΔAHC vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHC
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)
=>\(AE\cdot AC=AH^2\left(1\right)\)
Ta có: ΔADH~ΔAHB
=>\(\dfrac{AD}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AD\cdot AB\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AC=AD\cdot AB\)
=>\(\dfrac{AE}{AD}=\dfrac{AB}{AC}\)
Xét ΔAEB và ΔADC có
\(\dfrac{AE}{AD}=\dfrac{AB}{AC}\)
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔADC
=>\(\widehat{ABE}=\widehat{ACD}\)
Xét ΔMBD và ΔMCE có
\(\widehat{MBD}=\widehat{MCE}\)
\(\widehat{DMB}=\widehat{EMC}\)(hai góc đối đỉnh)
Do đó: ΔMBD~ΔMCE

a) Tam giác MNP có các đường cao MK, NI cắt nhau tại H nên H là trực tâm tam giác MNP => PH vuông góc MN hay PA vuông góc MN tại A.
b) Xét 2 tam giác MIN và MAP, ta có:
\(\widehat{MIN}=\widehat{MAP}=90^o\); \(\widehat{NMP}\) chung
\(\Rightarrow\Delta MIN\sim\Delta MAP\left(g.g\right)\)
c) Tương tự câu b), ta chứng minh được \(\Delta PIN\sim\Delta PKM\)
\(\Rightarrow\dfrac{PI}{PK}=\dfrac{PN}{PM}\Rightarrow\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
Xét tam giác PIK và PNM, ta có:
\(\dfrac{PI}{PN}=\dfrac{PK}{PM};\widehat{MPN}\) chung
\(\Rightarrow\Delta PIK\sim\Delta PNM\left(c.g.c\right)\)
\(\Rightarrow\widehat{PKI}=\widehat{PMN}\)
d) Xét tam giác MIH và MKP, ta có:
\(\widehat{MIH}=\widehat{MKP}=90^o\); \(\widehat{KMP}\) chung
\(\Rightarrow\Delta MIH\sim\Delta MKP\left(g.g\right)\)
\(\Rightarrow\dfrac{MI}{MK}=\dfrac{MH}{MP}\)
\(\Rightarrow MK.MH=MI.MP\)
e) Từ c), suy ra \(PK.PN=PI.PM\)
Do đó \(MH.MK+PK.PN\)
\(=MI.MP+PI.PM\)
\(=MP\left(MI+PI\right)\)
\(=MP^2\), ta có đpcm.
f) Từ câu d), ta có \(\widehat{PIK}=\widehat{PNM}\)
Tương tự câu d), ta cũng chứng minh được \(\Delta MIA\sim\Delta MNP\)
\(\Rightarrow\widehat{MIA}=\widehat{MNP}\)
\(\Rightarrow90^o-\widehat{MIA}=90^o-\widehat{MNP}\)
\(\Rightarrow\widehat{AIN}=\widehat{KIN}\)
\(\Rightarrow\) IN là tia phân giác \(\widehat{AIK}\)
g) Xét tam giác MBK và MKN, ta có:
\(\widehat{MBK}=\widehat{MKN}=90^o\); \(\widehat{NMK}\) chung
\(\Rightarrow\Delta MBK\sim\Delta MKN\left(g.g\right)\)
\(\Rightarrow\dfrac{MB}{MK}=\dfrac{MK}{MN}\)
\(\Rightarrow MK^2=MB.MN\)
Tương tự, ta cũng có \(MK^2=MC.MP\)
\(\Rightarrow MB.MN=MC.MP\left(=MK^2\right)\)
\(\Rightarrow\dfrac{MN}{MC}=\dfrac{MP}{MB}\)
Xét tam giác MNP và MCB, ta có:
\(\dfrac{MN}{MC}=\dfrac{MP}{MB};\) \(\widehat{NMP}\) chung
\(\Rightarrow\Delta MNP\sim\Delta MCB\left(c.g.c\right)\)
\(\Rightarrow\widehat{MNP}=\widehat{MCB}\)
Theo cmt, ta có \(\widehat{MIA}=\widehat{MNP}\)
\(\Rightarrow\widehat{MIA}=\widehat{MCB}\)
\(\Rightarrow\) IA//BC (2 góc đồng vị bằng nhau)
a: Xét ΔMNP có
NI,MK là các đường cao
NI cắt MK tại H
Do đó: H là trực tâm của ΔMNP
=>PH\(\perp\)MN tại A
b: Xét ΔMIN vuông tại I và ΔMAP vuông tại A có
\(\widehat{IMN}\) chung
Do đó: ΔMIN~ΔMAP
c: Xét ΔPKM vuông tại K và ΔPIN vuông tại I có
\(\widehat{KPM}\) chung
Do đó: ΔPKM~ΔPIN
=>\(\dfrac{PK}{PI}=\dfrac{PM}{PN}\)
=>\(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
Xét ΔPIK và ΔPNM có
\(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
\(\widehat{IPK}\) chung
Do đó: ΔPIK~ΔPNM
=>\(\widehat{PKI}=\widehat{PMN}\)
d: Xét ΔMIH vuông tại H và ΔMKP vuông tại K có
\(\widehat{IMH}\) chung
Do đó: ΔMIH~ΔMKP
=>\(\dfrac{MI}{MK}=\dfrac{MH}{MP}\)
=>\(MI\cdot MP=MK\cdot MH\)
e: \(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
=>\(PI\cdot PM=PN\cdot PK\)
\(MH\cdot MK+PK\cdot PN\)
\(=MI\cdot MP+IP\cdot MP\)
=MP(MI+IP)
=MP^2

a
ta có: MN\(\perp\)AC
AB\(\perp\)AC
Do đó: MN//AB
ta có: MP\(\perp\)AB
AC\(\perp\)AB
Do đó: MP//AC
Xét ΔBMP vuông tại P và ΔMCN vuông tại N có
\(\widehat{MBP}=\widehat{CMN}\)(hai góc đồng vị, MN//AB)
Do đó: ΔBMP~ΔMCN
b: Xét ΔBAC có MP//AC
nên \(\dfrac{MP}{AC}=\dfrac{BM}{BC}\)
=>\(\dfrac{MP}{12}=\dfrac{6}{15}=\dfrac{2}{5}\)
=>\(MP=12\cdot\dfrac{2}{5}=4,8\left(cm\right)\)
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CM}{CB}\)
=>\(\dfrac{MN}{9}=\dfrac{9}{15}=\dfrac{3}{5}\)
=>MN=9*3/5=5,4(cm)
Xét tứ giác APMN có \(\widehat{APM}=\widehat{ANM}=\widehat{PAN}=90^0\)
nên APMN là hình chữ nhật
=>\(AM^2=MN^2+MP^2=5,4^2+4,8^2=52,2\)
=>\(AM=\sqrt{52,2}\left(cm\right)\)

a) \(4x^2-1=\left(2x+1\right)\left(3x-5\right)\)
\(\Leftrightarrow\left(2x\right)^2-1^2=\left(2x+1\right)\left(3x-5\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(2x-1\right)-\left(2x+1\right)\left(3x-5\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(2x-1-3x+5\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(4-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\4=x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=4\end{matrix}\right.\)
Vậy: ...
b) \(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}=10\)
\(\Leftrightarrow\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}-10=0\)
\(\Leftrightarrow\left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0\)
\(\Leftrightarrow\dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\)
\(\Leftrightarrow x-100=0\)
\(\Leftrightarrow x=100\)
Vậy: ...

a) Bảng giá trị
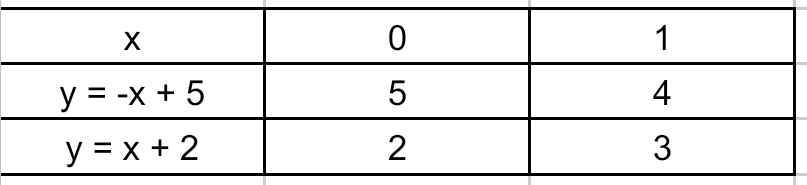 Đồ thị:
Đồ thị:
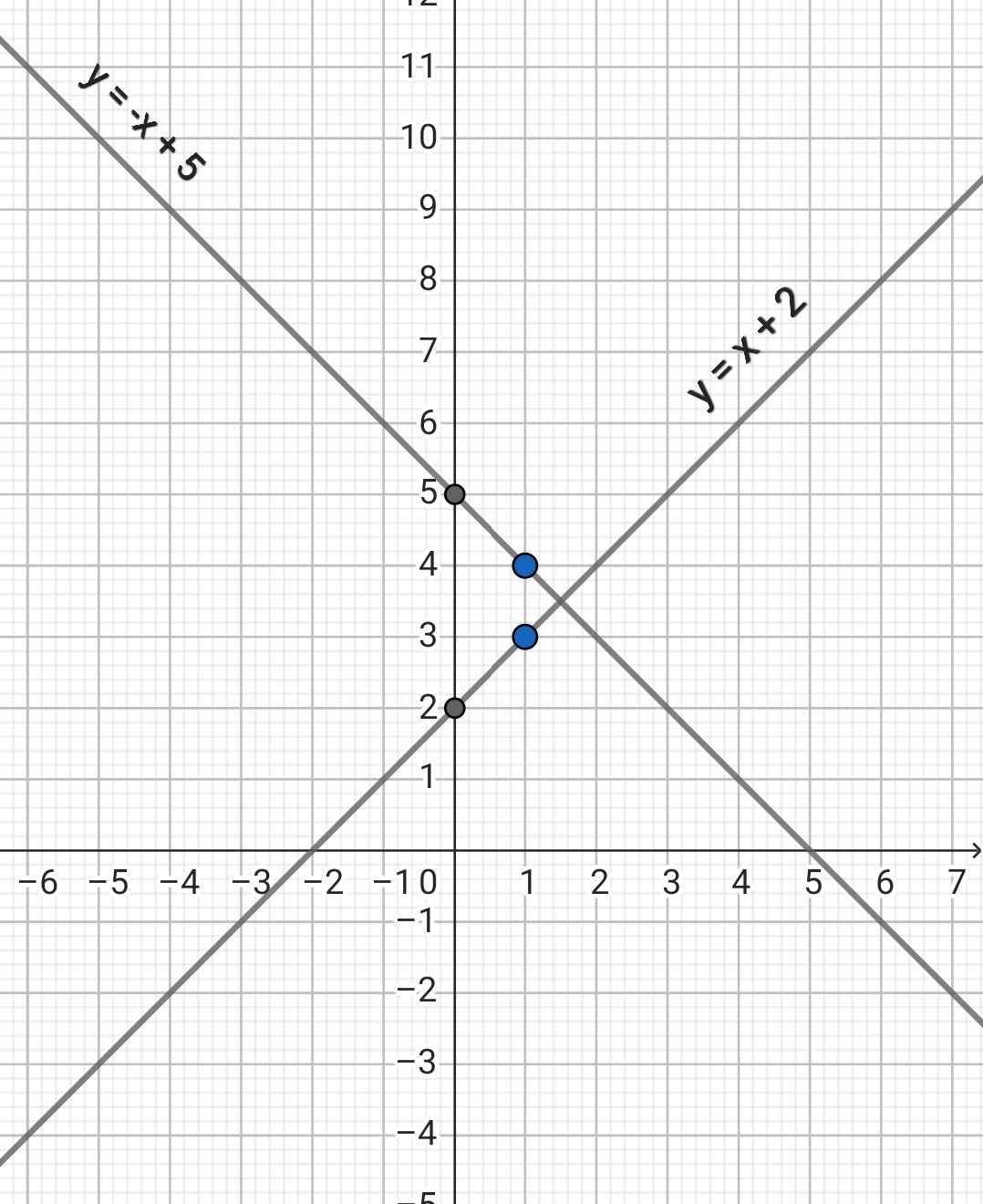
b) Phương trình hoành độ giao điểm của (d₁) và (d₂):
-x + 5 = x + 2
-x - x = 2 - 5
-2x = -3
x = 3/2
Thay x = 3/2 vào (d₂), ta có:
y = 3/2 + 2 = 7/2
Vậy tọa độ giao điểm M(3/2; 7/2)
c) Gọi (d₃): y = ax + b (a ≠ 0) là đồ thị của hàm số cần tìm
Do (d₃) // (d₁) nên a = -1
⇒ (d₃): y = -x + b
Do (d₃) đi qua K(-4; 2) nên thay tọa độ của K(-4; 2) vào (d₃), ta có:
-(-4) + b = 2
b = 2 - 4
b = -2
Vậy hàm số cần tìm là:
y = -x - 2
a) Đồ thị hs:`y=-2x+5` cắt `Ox(5/2;0)` và cắt `Oy(0;5)`
Đồ thị hs: `y=x+2` cắt `Ox(-2;0)` và cắt `Oy(0;2)`
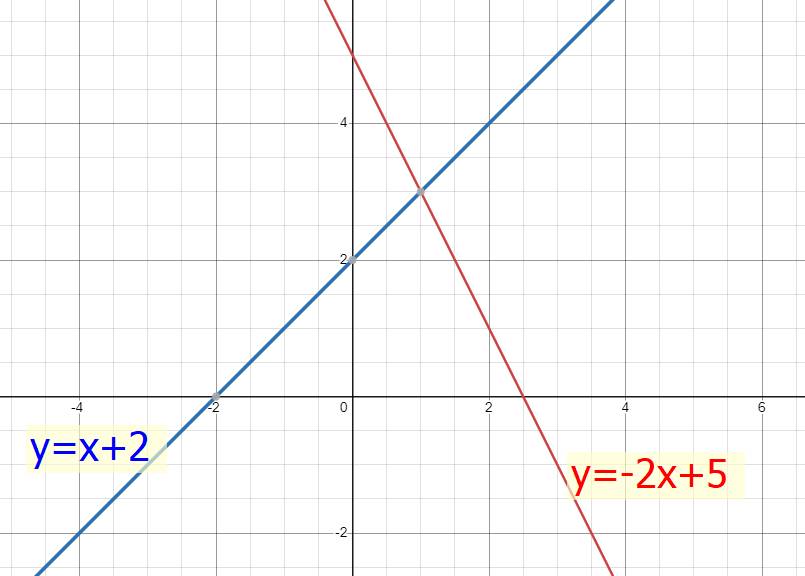
b) Ta có pt hoành độ giao điểm của (d1) và (d2):
\(-2x+5=x+2\)
\(\Leftrightarrow x+2x=5-2\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\)
Thay `x=1` vào `(d_2)` ta có: \(y=1+2=3\)
`=>M(1;3)`
c) Hàm số `y=ax+b` có đồ thị song song với `(d_1):y=-2x+5`
`=>a=-2`
`=>y=-2x+b`
Mà hàm số này đi qua điểm `K(-4;2)` ta thay `x=-4` và `y=2` vào ta có:
`2=-2*(-4)+b`
`<=>2=8+b`
`<=>b=2-8=-6`
Vậy hàm số đó là: `y=-2x-6`



a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔAFC
b: ta có: ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{EAF}\) chung
Do đó: ΔAEF~ΔABC
=>\(\widehat{AEF}=\widehat{ABC}\)
c: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó; ΔHFB~ΔHEC
=>\(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)
=>\(\dfrac{HF}{HB}=\dfrac{HE}{HC}\)
Xét ΔHFE và ΔHBC có
\(\dfrac{HF}{HB}=\dfrac{HE}{HC}\)
\(\widehat{FHE}=\widehat{BHC}\)(hai góc đối đỉnh)
Do đó: ΔHFE~ΔHBC