Bài 7) Cho tứ giác ABCD , hai đường chéo AC và BD cắt nhau tại 0
góc ABD = góc ACD, gọi E là giao điểm của của hai đường thẳng AD và BC
a) Chứng minh: AAOB đồng dạng ADOC
b) Chứng minh: AAOD đồng dạng ABOC
с)
Chứng minh: EA.ED = EB.EC
Bài 8) Cho AABC có 3 đường cao AD,BE, CF đồng quy tại H.
Chứng minh: AH.DH = BH.EH = CH.FH
Giải giúp mình với, mình cảm iwn nhiều ạ!


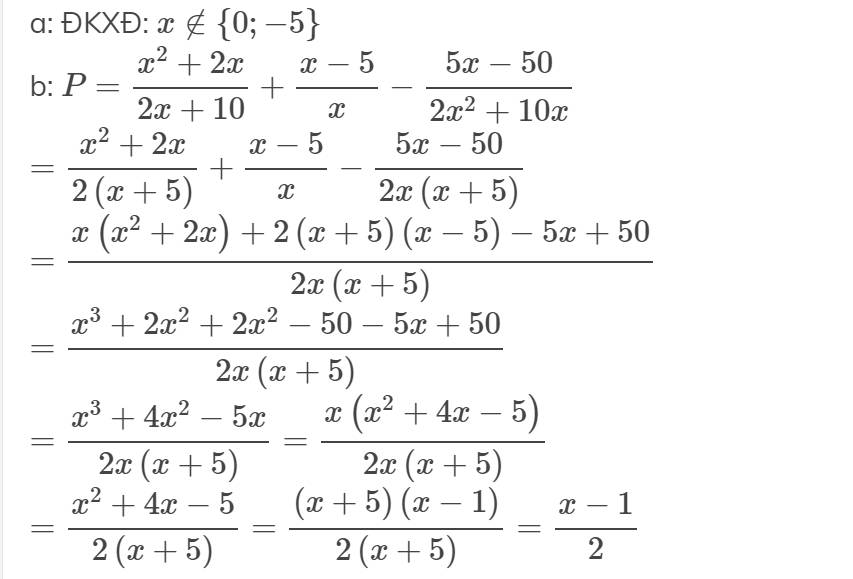


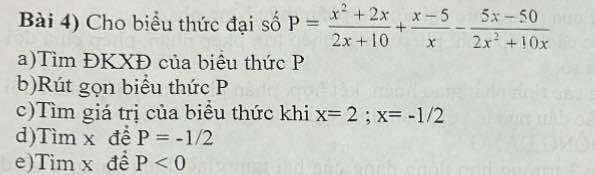

Bài 7:
a: Xét ΔOBA và ΔOCD có
\(\widehat{OBA}=\widehat{OCD}\)
\(\widehat{BOA}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOBA~ΔOCD
b: Ta có: ΔOBA~ΔOCD
=>\(\dfrac{OB}{OC}=\dfrac{OA}{OD}\)
=>\(\dfrac{OB}{OA}=\dfrac{OC}{OD}\)
Xét ΔOBC và ΔOAD có
\(\dfrac{OB}{OA}=\dfrac{OC}{OD}\)
\(\widehat{BOC}=\widehat{AOD}\)(hai góc đối đỉnh)
Do đó: ΔOBC~ΔOAD
c: Ta có: ΔOBC~ΔOAD
=>\(\widehat{OCB}=\widehat{ODA}\)
Xét ΔEBD và ΔEAC có
\(\widehat{EDB}=\widehat{ECA}\)
\(\widehat{E}\) chung
Do đó: ΔEBD~ΔEAC
=>\(\dfrac{EB}{EA}=\dfrac{ED}{EC}\)
=>\(EB\cdot EC=EA\cdot ED\)
Bài 8:
Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{EHA}=\widehat{DHB}\)(hai góc đối đỉnh)
Do đó: ΔHEA~ΔHDB
=>\(\dfrac{HE}{HD}=\dfrac{HA}{HB}\)
=>\(HE\cdot HB=HD\cdot HA\)(1)
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔHFB~ΔHEC
=>\(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)
=>\(HF\cdot HC=HB\cdot HE\left(2\right)\)
Từ (1) và (2) suy ra \(HA\cdot HD=HF\cdot HC=HB\cdot HE\)
Khi giải toán hình Thịnh cần có thêm hình vẽ nhé.