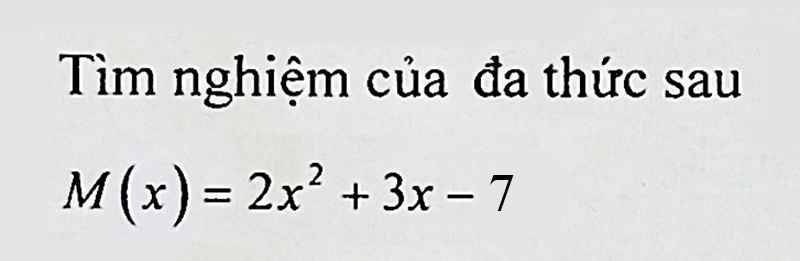
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x+2\right)\left(3-2x\right)+x=2x^3-3\)
=>\(3x-2x^2+6-4x+x=2x^3-3\)
=>\(-2x^2+6-2x^3+3=0\)
=>\(-2x^3-2x^2+9=0\)
=>\(2x^3+2x^2-9=0\)
=>\(x\simeq1,376\)

a: Số tiền phải trả khi mua 1 đôi dép là: \(x\cdot\left(1-40\%\right)=0,6x\left(đồng\right)\)
b: Số tiền phải trả trong đợt khuyến mãi là:
\(0,6\cdot300000=180000\left(đồng\right)\)

M(x)=x^2-2x+5x^2+3x-x^2
=5x^2+x
b) Thế x=-2 và M=5x^2+x vào đa thức A, ta có:
A= [5(-2)^2+(-2)]+2(-2)-8
A=6
Vậy đa thức A có giá trị bằng 6 tại x=-2

a: Xét ΔAMD và ΔCMB có
MA=MC
\(\widehat{AMD}=\widehat{CMB}\)
MD=MB
Do đó: ΔAMD=ΔCMB
b: Xét ΔMAB và ΔMCD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó: ΔMAB=ΔMCD
=>AB=CD
ΔMAB=ΔMCD
=>\(\widehat{MAB}=\widehat{MCD}\)
=>AB//CD
c: TA có: \(AN=\dfrac{AB}{2}\)
\(CE=\dfrac{CD}{2}\)
mà AB=CD
nên AN=CE
Xét ΔMAN và ΔMCE có
MA=MC
\(\widehat{MAN}=\widehat{MCE}\)
AN=CE
DO đó: ΔMAN=ΔMCE
=>\(\widehat{AMN}=\widehat{CME}\)
mà \(\widehat{AMN}+\widehat{NMC}=180^0\)(hai góc kề bù)
nên \(\widehat{CME}+\widehat{NMC}=180^0\)
=>N,M,E thẳng hàng
mà NM=ME(ΔMAN=ΔMCE)
nên M là trung điểm của NE

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
b:
ΔAHB=ΔAHC
=>HB=HC
Xét ΔHMB vuông tại M và ΔHNC vuông tại N có
HB=HC
\(\widehat{HBM}=\widehat{HCN}\)
Do đó: ΔHMB=ΔHNC
=>HM=HN và \(\widehat{MHB}=\widehat{NHC}\)
c: Xét ΔHNC và ΔHPC có
HN=HP
\(\widehat{NHC}=\widehat{PHC}\left(=\widehat{MHB}\right)\)
HC chung
Do đó: ΔHNC=ΔHPC
=>\(\widehat{HCP}=\widehat{HCN}\)
=>\(\widehat{HCP}=\widehat{CBA}\)
=>CP//BA



Đặt M(x)=0
=>\(2x^2+3x-7=0\)(1)
\(\text{Δ}=3^2-4\cdot2\cdot\left(-7\right)=9+56=65>0\)
Do đó: Phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{65}}{2\cdot2}=\dfrac{-3-\sqrt{65}}{4}\\x_2=\dfrac{-3+\sqrt{65}}{4}\end{matrix}\right.\)