Y=-(5x-8+9x)+3 có phải là hàm số bậc nhất không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho đường thẳng (d): (y=(2m+1)x-2) với m là tham số và (m\ne-\frac{1}{2}.) Khoảng cách từ (A(-2;1)) đến đường thẳng d được tính theo công thức:
[\sqrt{(-2-(2m+1)(-2))^2+(1-(2m+1)(-2))^2}]
[\sqrt{(16m^2+20m+4)^2+(24m+4)^2}]
[\sqrt{256m^4+640m^3+320m^2+576m^2+960m+16}]
[\sqrt{256m^4+1216m^3+1536m^2+960m+16}]
[\sqrt{16m^2(16m^2+79m+96)+4(16m^2+79m+96)}]
[\sqrt{(4m+7)^2(4m+16)}]
Theo đề bài, khoảng cách này bằng (\frac{1}{\sqrt{2}}.) Do đó, ta có phương trình:
[\sqrt{(4m+7)^2(4m+16)}=\frac{1}{\sqrt{2}}]
Từ đây, ta được phương trình bậc hai:
[(4m+7)^2(4m+16)=1 ]
Giải phương trình này, ta được hai nghiệm:
[m=-\frac{3}{2}\pm\frac{\sqrt{3}}{2} ]
Do (m\ne-\frac{1}{2},) ta có nghiệm duy nhất là:
[m=-\frac{3}{2}+\frac{\sqrt{3}}{2}=\frac{5}{7} ]
Vậy, tổng các giá trị của m thỏa mãn bài toán là [\frac{5}{7}.]

Tổng 2 vận tốc:
210:2=105(km/h)
Vận tốc xe máy:
(105 - 15):2= 45(km/h)
Đ.số: xe máy có vận tốc 45km/h

Lời giải:
PT hoành độ giao điểm:
$(m^2+1)x-12m+5=x+5$
$\Leftrightarrow m^2x-12m=0(*)$
Để 2 đths cắt nhau tại 1 điểm có hoành độ $x=2$ thì $x=2$ phải là nghiệm của $(*)$
$\Rightarrow m^2.2-12m=0$
$\Leftrightarrow 2m(m-6)=0$
$\Rightarrow m=0$ hoặc $m=6$


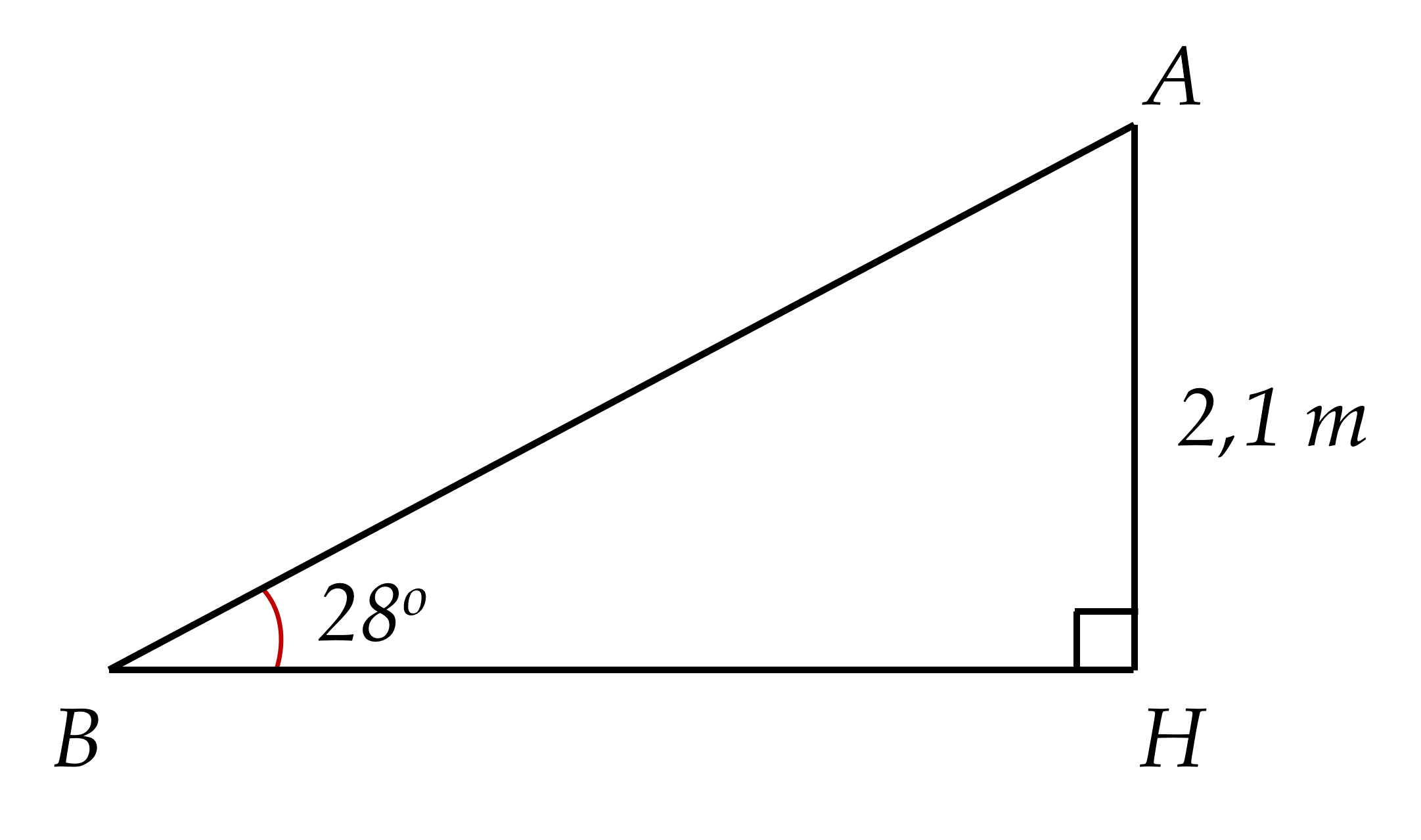
1) Xét △ABH vuông tại H có:
\(\sin\widehat{ABH}=\dfrac{AH}{AB}\)(tỉ số lượng giác)
⇒ \(AB=\dfrac{AH}{\sin\widehat{ABH}}=\dfrac{2,1}{\sin28^o}\approx4,5\left(m\right)\)
Vậy độ dài của mặt cầu trượt khoảng 4,5m.
2)
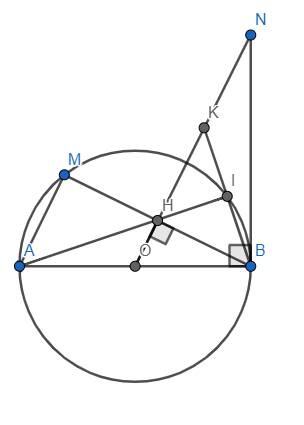
a) Xét △AMB có: A, M, B ∈ (O) (gt)
AB là đường kính của (O) (gt)
⇒ △AMB vuông tại M(ĐL về sự xác định của đường tròn)
Xét △AMB vuông tại M có: O là trung điểm AB(gt)
OH // AM (⊥ MB)
⇒ OH là đường trung bình của △AMB
⇒ H là trung điểm của MB (t/c)(đpcm)
Xét △NMB có: H là trung điểm của MB(cmt)
NH ⊥ MB(do N ∈ OH ⊥ MB)
⇒ NH là đường trung tuyến đồng thời cũng là đường cao trong △NMB
⇒ △NMB cân tại N(t/c △ cân)
⇒ NM = NB(t/c △ cân)
Xét △NMO và △NBO có:
ON chung
NM = NB(cmt)
OM = OB(= R)
⇒ △NMO = △NBO (c.c.c)
⇒ \(\widehat{NMO}=\widehat{NBO}=90^o\)
⇒ NM ⊥ MO
Mà OM = R
⇒ MN là tiếp tuyến của đường tròn (O; R) (đpcm)
b) Xét △MAB và △HBN có:
\(\widehat{AMB}=\widehat{BHN}=90^o\)
\(\widehat{MBA}=\widehat{HNB}\) (do cùng phụ với \(\widehat{NOB}\))
⇒ △MAB ∼ △HBN (g.g)(đpcm)

Bài 2:
1) Thay m = 1(TMĐK) vào hàm số y = (m - 2)x + m + 3 có
⇒ y = (1 - 2)x + 1 + 3
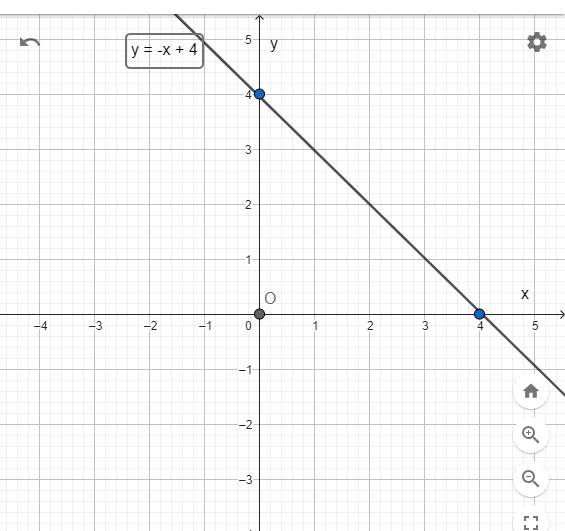
⇒ y = -x + 4
Xét (d) : y = -x + 4 có bảng
| x | 0 | 4 |
| y | 4 | 0 |
| Điểm | (0; 4) | (4; 0) |
2) Để hai đường thẳng và cắt nhau tại một điểm trên trục tung thì
⇒\(\left\{{}\begin{matrix}m-2\ne5\\m+3=-1\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}m\ne7\\m=-2\end{matrix}\right.\)(TM) ⇒ m = -2
Vậy m = -2 thì hai đường thẳng (d)
và cắt nhau tại một điểm trên trục tung.
Bài 2:
1) Thay m = 1(TMĐK) vào hàm số y = (m - 2)x + m + 3 có
⇒ y = (1 - 2)x + 1 + 3
⇒ y = -x + 4
Xét (d) : y = -x + 4 có bảng
| x | 0 | 4 |
| y | 4 | 0 |
| Điểm | (0; 4) | (4; 0) |

2) Để hai đường thẳng và cắt nhau tại một điểm trên trục tung thì
⇒\(\left\{{}\begin{matrix}m-2\ne5\\m+3=-1\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}m\ne7\\m=-2\end{matrix}\right.\)(TM) ⇒ m = -2
Vậy m = -2 thì hai đường thẳng (d)
và cắt nhau tại một điểm trên trục tung.


Hàm số bậc nhất có dạng: \(y=ax+b\left(a\ne0\right)\)
Có: \(y=-\left(5x-8+9x\right)+3=-5x+8-9x+3=-14x+11\)
=> Là hàm số bậc nhất.