Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P\left(x\right)=\left(x-b\right)\left(x^2-5x+a\right)\)
Q(x)=x3+125
Để P(x)=Q(x) thì \(\left(x-b\right)\left(x^2-5x+a\right)=x^3+125\)
=>\(x^3-5x^2+a\cdot x-bx^2+5b\cdot x-ab=x^3+125\)
=>\(x^2\left(-b-5\right)+x\left(a+5b\right)-ab=125\)
=>\(\left\{{}\begin{matrix}-b-5=0\\a+5b=0\\-ab=125\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-5\\a=-5b=-5\cdot\left(-5\right)=25\\-25\cdot\left(-5\right)=125\left(đúng\right)\end{matrix}\right.\)
=>a=25 và b=-5

Câu 1: B
Câu 2: C
Câu 3: C
Câu 4: B
Câu 5: B
Câu 6: D
Câu 7: A
Câu 8: A
Câu 9: D
Câu 10: A


A = 2(x + 2) + 3/11
Do (x + 2)≥ 0
⇒ 2(x + 2) ≥ 0
⇒ 2(x + 2) + 3/11 ≥ 3/11
A nhỏ nhất là 3/11 khi x =-2
--------
B = 5/17 - 3(x - 5)
Do (x - 5) ≥ 0
⇒ 3(x - 5) ≥ 0
⇒ -3(x - 5) ≤ 0
⇒ 5/17 - 3(x - 5) ≤ 5/17
Vậy B lớn nhất là 5/17 khi x = 5


\(\dfrac{x}{2}=\dfrac{y}{5}=2z\)
=>\(\dfrac{x}{4}=\dfrac{y}{10}=\dfrac{z}{1}=k\)
=>x=4k; y=10k; z=k
\(2x^2+y^2-4z^2=2\cdot\left(4k\right)^2+\left(10k\right)^2-4k^2\)
\(=32k^2+100k^2-4k^2=128k^2\)

a: Xét ΔAMB và ΔNMC có
MA=MN
góc AMB=góc NMC
MB=MC
Do đó: ΔAMB=ΔNMC
b: Xét ΔBAI có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAI cân tại B
=>BA=BI=CN
Đúng thì tick cho mk nha

a:
Sửa đề: \(N\left(x\right)=3x^3-7x^2-x+\dfrac{3}{2}\)
M(x)+N(x)
\(=3x^3-7x^2+\dfrac{4}{5}x-\dfrac{1}{5}+3x^3-7x^2-x+\dfrac{3}{2}\)
\(=6x^3-14x^2-\dfrac{1}{5}x+\dfrac{13}{10}\)
b: H(x)=M(x)-N(x)
\(=3x^3-7x^2+\dfrac{4}{5}x-\dfrac{1}{5}-3x^3+7x^2+x-\dfrac{3}{2}\)
\(=\dfrac{9}{5}x-\dfrac{17}{10}\)
c: Đặt H(x)=0
=>\(\dfrac{9}{5}x-\dfrac{17}{10}=0\)
=>\(\dfrac{9}{5}x=\dfrac{17}{10}\)
=>\(x=\dfrac{17}{10}:\dfrac{9}{5}=\dfrac{17}{10}\cdot\dfrac{5}{9}=\dfrac{17}{18}\)
d: \(P\left(-1\right)=\left(-1\right)^3-3\cdot\left(-1\right)^2+3\cdot\left(-1\right)-1+2\cdot\left(-1\right)^3+\left(-1\right)^2-\left(-1\right)+5\)
\(=-1-3-3-1-2+1+1+5\)
=-3<0
=>x=-1 không là nghiệm của P(x)
\(P\left(x\right)=x^3-3x^2+3x-1+2x^3+x^2-x+5\)
\(=\left(x^3+2x^3\right)+\left(-3x^2+x^2\right)+\left(3x-x\right)+\left(-1+5\right)\)
\(=3x^3-2x^2+2x+4\)


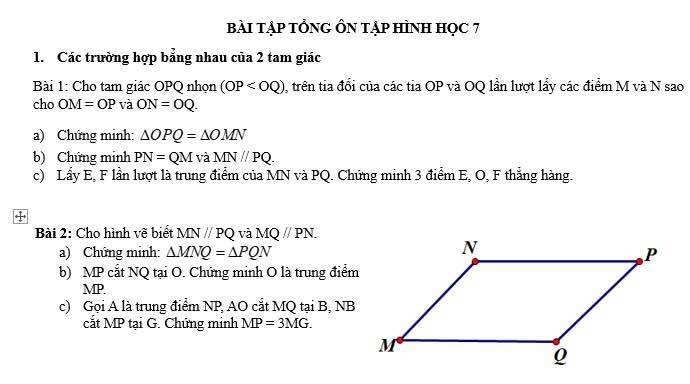
Bài 2:
a: Xét ΔMNQ và ΔPQN có
\(\widehat{MNQ}=\widehat{PQN}\)(MN//PQ)
NQ chung
\(\widehat{MQN}=\widehat{PNQ}\)(MQ//NP)
Do đó: ΔMNQ=ΔPQN
b:
ΔMNQ=ΔPQN
=>MQ=PN; MN=PQ
Xét ΔOMN và ΔOPQ có
\(\widehat{OMN}=\widehat{OPQ}\)(MN//PQ)
MN=PQ
\(\widehat{ONM}=\widehat{OQP}\)(MN//PQ)
Do đó: ΔOMN=ΔOPQ
=>OM=OP
=>O là trung điểm của MP
c: ΔOMN=ΔOPQ
=>ON=OQ
Xét ΔOAN và ΔOBQ có
\(\widehat{ONA}=\widehat{OQB}\)(NA//BQ)
ON=OQ
\(\widehat{AON}=\widehat{BOQ}\)(hai góc đối đỉnh)
Do đó: ΔOAN=ΔOBQ
=>AN=BQ
=>\(BQ=\dfrac{1}{2}MQ\)
=>B là trung điểm của MQ
Xét ΔMQN có
NB,MO là các đường trung tuyếm
NB cắt MO tại G
Do đó: G là trọng tâm của ΔMQN
=>\(MG=\dfrac{2}{3}MO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot MP=\dfrac{1}{3}MP\)
=>MP=3MG
Bài 1:
a: Xét ΔOPQ và ΔOMN có
OP=OM
\(\widehat{POQ}=\widehat{MON}\)(hai góc đối đỉnh)
OQ=ON
Do đó: ΔOPQ=ΔOMN
b: ΔOPQ=ΔOMN
=>\(\widehat{OPQ}=\widehat{OMN}\)
=>PQ//MN
Xét ΔONP và ΔOQM có
ON=OQ
\(\widehat{NOP}=\widehat{QOM}\)(hai góc đối đỉnh)
OP=OM
Do đó: ΔONP=ΔOQM
=>NP=QM
c: ΔOMN=ΔOPQ
=>MN=PQ
mà \(NF=\dfrac{NM}{2};QE=\dfrac{QP}{2}\)
nên NF=QE
Xét ΔFNO và ΔEQO có
FN=EQ
\(\widehat{FNO}=\widehat{EQO}\)
NO=QO
Do đó: ΔFNO=ΔEQO
=>\(\widehat{FON}=\widehat{EOQ}\)
=>\(\widehat{FON}+\widehat{FOE}=180^0\)
=>N,O,E thẳng hàng