Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB~ΔCAB
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100=10^2\)
=>BC=10(cm)
ΔAHB~ΔCAB
=>\(\dfrac{AH}{CA}=\dfrac{HB}{AB}=\dfrac{AB}{CB}\)
=>\(\dfrac{AH}{8}=\dfrac{HB}{6}=\dfrac{6}{10}=\dfrac{3}{5}\)
=>\(AH=8\cdot\dfrac{3}{5}=4,8\left(cm\right);HB=6\cdot\dfrac{3}{5}=\dfrac{18}{5}=3,6\left(cm\right)\)
c: Ta có: \(\widehat{BHE}+\widehat{DHE}+\widehat{DHC}=180^0\)
=>\(\widehat{BHE}+\widehat{DHC}+90^0=180^0\)
=>\(\widehat{BHE}+\widehat{DHC}=90^0\)
mà \(\widehat{DHC}+\widehat{DHA}=\widehat{CHA}=90^0\)
nên \(\widehat{BHE}=\widehat{DHA}\)
Xét ΔBHE và ΔAHD có
\(\widehat{BHE}=\widehat{DHA}\)
\(\widehat{HBE}=\widehat{HAD}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔBHE~ΔAHD

a: Thay x=3 vào A, ta được:
\(A=\dfrac{3^2}{3+3}=\dfrac{9}{6}=\dfrac{3}{2}\)
b: \(B=\dfrac{3x}{x-1}-\dfrac{2x}{x+1}+\dfrac{x-3}{1-x^2}\)
\(=\dfrac{3x}{x-1}-\dfrac{2x}{x+1}-\dfrac{x-3}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{3x\left(x+1\right)-2x\left(x-1\right)-x+3}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{3x^2+3x-2x^2+2x-x+3}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+4x+3}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x+3\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+3}{x-1}\)
c: \(P=A\cdot B=\dfrac{x+3}{x-1}\cdot\dfrac{x^2}{x+3}=\dfrac{x^2}{x-1}\)
Để P=4 thì \(\dfrac{x^2}{x-1}=4\)
=>\(x^2=4\left(x-1\right)=4x-4\)
=>\(x^2-4x+4=0\)
=>(x-2)^2=0
=>x-2=0
=>x=2(nhận)

a: Xét ΔBDE vuông tại E và ΔBCD vuông tại D có
\(\widehat{DBE}\) chung
Do đó: ΔBDE~ΔBCD
b: Xét ΔBFD vuông tại F và ΔBDA vuông tại D có
\(\widehat{FBD}\) chung
Do đó: ΔBFD~ΔBDA
=>\(\dfrac{BF}{BD}=\dfrac{BD}{BA}\)
=>\(BD^2=BF\cdot BA\)
c: Ta có: ΔBDE~ΔBCD
=>\(\dfrac{BD}{BC}=\dfrac{BE}{BD}\)
=>\(BD^2=BE\cdot BC\)
=>\(BF\cdot BA=BE\cdot BC\)
=>\(\dfrac{BF}{BC}=\dfrac{BE}{BA}\)
Xét ΔBFE và ΔBCA có
\(\dfrac{BF}{BC}=\dfrac{BE}{BA}\)
\(\widehat{FBE}\) chung
Do đó: ΔBFE~ΔBCA
=>\(\widehat{BFE}=\widehat{BCA}\)
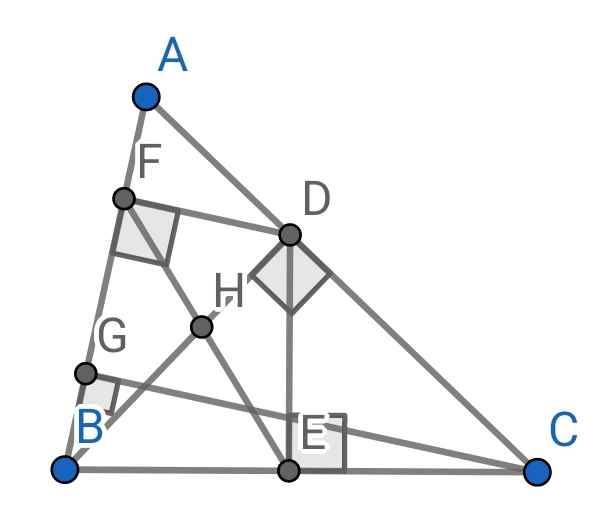
a) Xét hai tam giác vuông: ∆BDE và ∆BCD có:
∠B chung
⇒ ∆BDE ∽ ∆BCD (g-g)
b) Xét hai tam giác vuông: ∆BFD và ∆BDA có:
∠B chung
⇒ ∆BFD ∽ ∆BDA (g-g)
⇒ BF/BD = BD/BA
⇒ BD² = BF.BA
c) Do ∆BDE ∽ ∆BCD (cmt)
⇒ BD/BC = BE/BD
⇒ BD² = BE.BC
Mà BD² = BF.BA (cmt)
⇒ BF.BA = BE.BC
⇒ BF/BC = BE/BA
Xét ∆BFE và ∆BCA có:
BA/BC = BE/BA (cmt)
∠B chung
⇒ ∆BFE ∽ ∆BCA (c-g-c)
d) Em xem lại đề, đề thiếu vì hình bị mất

1: Xét ΔCEH vuông tại E và ΔCAB vuông tại A có
\(\widehat{ECH}\) chung
Do đó: ΔCEH~ΔCAB
2: Xét tứ giác AHEB có \(\widehat{HAB}+\widehat{HEB}=90^0+90^0=180^0\)
nên AHEB là tứ giác nội tiếp
=>\(\widehat{HBC}=\widehat{EAC}\)
3:
Xét ΔIBA và ΔIEH có
\(\widehat{IBA}=\widehat{IEH}\)(ABEH là tứ giác nội tiếp)
\(\widehat{BIA}=\widehat{EIH}\)(hai góc đối đỉnh)
Do đó; ΔIBA~ΔIEH
=>\(\dfrac{AB}{EH}=\dfrac{AI}{HI}\)
=>\(AB\cdot HI=AI\cdot HE\)

a: \(C=\left(\dfrac{2+x}{2-x}+\dfrac{4x^2}{4-x^2}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-x}{2x-x^2}\)
\(=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right)\cdot\dfrac{x\left(2-x\right)}{x\left(x-1\right)}\)
\(=\dfrac{-\left(x+2\right)^2-4x^2+\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{2-x}{x-1}\)
\(=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{\left(x+2\right)}\cdot\dfrac{-1}{x-1}\)
\(=\dfrac{-4x^2-8x}{\left(x+2\right)\left(x-1\right)}\cdot\left(-1\right)=\dfrac{4x\left(x+2\right)}{\left(x+2\right)\left(x-1\right)}=\dfrac{4x}{x-1}\)
b: Để C=1 thì 4x=x-1
=>3x=-1
=>\(x=-\dfrac{1}{3}\left(nhận\right)\)
c: Để C là số nguyên thì \(4x⋮x-1\)
=>\(4x-4+4⋮x-1\)
=>\(4⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{2;0;3;-1;5;-3\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{3;-1;5;-3\right\}\)

a: Ta có;ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+12^2=20^2\)
=>\(AC^2=20^2-12^2=256=16^2\)
=>AC=16(cm)
Xét ΔBAC có BM là phân giác
nên \(\dfrac{AM}{AB}=\dfrac{CM}{CB}\)
=>\(\dfrac{AM}{12}=\dfrac{CM}{20}\)
=>\(\dfrac{AM}{3}=\dfrac{CM}{5}\)
mà AM+CM=AC=16cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{CM}{5}=\dfrac{AM+CM}{3+5}=\dfrac{16}{8}=2\)
=>\(CM=2\cdot5=10\left(cm\right)\)
b: Ta có: MI\(\perp\)BC
AK\(\perp\)BC
Do đó: MI//AK
Xét ΔCAK có MI//AK
nên \(\dfrac{CI}{IK}=\dfrac{CM}{MA}\)
mà \(\dfrac{CM}{MA}=\dfrac{CB}{BA}\)
nên \(\dfrac{CI}{IK}=\dfrac{CB}{BA}\)
=>\(AB\cdot IC=IK\cdot BC\)

a: Đặt F=C*x+b
Thay x=0 và F=32 vào F=Cx+b, ta được:
\(0\cdot C+b=32\)
=>b=32
=>F=Cx+32
Thay x=1 và y=32+1,8=33,8 vào F=x*C+32, ta được:
\(x\cdot1+32=33,8\)
=>x+32=33,8
=>x=1,8
Vậy: F=1,8C+32
b: Nước sôi ở nhiệt độ 100 độ C
=>\(F=1,8\cdot100+32=180+32=212^0F\)

a: Ta có; ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100=10^2\)
=>BC=10(cm)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{6}=\dfrac{CD}{10}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{5}\)
mà AD+CD=AC=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{8}{8}=1\)
=>\(AD=3\cdot1=3\left(cm\right)\)
b: Vì BD là phân giác trong tại B của ΔABC
và BD\(\perp\)BE
nênBE là phân giác ngoài tại B của ΔABC
Xét ΔABC có BE là phân giác ngoài tại B
nên \(\dfrac{EA}{EC}=\dfrac{AB}{BC}\)
mà \(\dfrac{AB}{BC}=\dfrac{DA}{DC}\)
nên \(\dfrac{EA}{EC}=\dfrac{DA}{DC}\)
=>\(EA\cdot DC=DA\cdot EC\)

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
=>AD=AE và BD=CE
Xét ΔAEM vuông tại E và ΔADM vuông tại D có
AM chung
AE=AD
Do đó: ΔAEM=ΔADM
=>ME=MD
b: ĐƯờng thẳng vuông góc với CE ở đâu vậy bạn?
c: Xét ΔMKE vuông tại K và ΔMHD vuông tại H có
ME=MD
\(\widehat{KME}=\widehat{HMD}\)(hai góc đối đỉnh)
Do đó: ΔMKE=ΔMHD
=>EK=HD và MK=MH
Xét ΔMKP vuông tại K và ΔMHP vuông tại H có
MK=MH
MP chung
Do đó: ΔMKP=ΔMHP
=>PH=PK
Ta có: ME+MC=EC
MD+MB=DB
mà ME=MD và EC=DB
nên MC=MB
Ta có: MK+KB=MB
MH+HC=MC
mà MK=MH và MB=MC
nên KB=HC
Xét ΔPKB vuông tại K và ΔPHC vuông tại H có
PK=PH
KB=HC
Do đó: ΔPKB=ΔPHC
=>PB=PC
=>P nằm trên đường trung trực của BC(1)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(2)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,M,P thẳng hàng

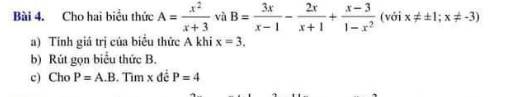


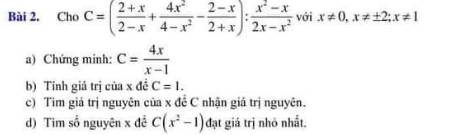



a: \(\left(x+5\right)\left(x-1\right)=2x\left(x-1\right)\)
=>\(2x\left(x-1\right)-\left(x+5\right)\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(2x-x-5\right)=0\)
=>(x-1)(x-5)=0
=>\(\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
b: \(3\left(x-1\right)\left(2x-1\right)=5\left(x+8\right)\left(x-1\right)\)
=>\(\left(x-1\right)\left(6x-3\right)-\left(x-1\right)\left(5x+40\right)=0\)
=>\(\left(x-1\right)\left(6x-3-5x-40\right)=0\)
=>(x-1)(x-43)=0
=>\(\left[{}\begin{matrix}x=1\\x=43\end{matrix}\right.\)
c: \(\left(x^2-5x+7\right)^2-\left(2x-5\right)^2=0\)
=>\(\left(x^2-5x+7-2x+5\right)\left(x^2-5x+7+2x-5\right)=0\)
=>\(\left(x^2-7x+12\right)\left(x^2-3x+2\right)=0\)
=>(x-3)(x-4)(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=3\\x=4\\x=1\\x=2\end{matrix}\right.\)
d: \(x^3-5x^2+6x=0\)
=>\(x\left(x^2-5x+6\right)=0\)
=>x(x-2)(x-3)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\\x=3\end{matrix}\right.\)
e: \(\left(x+3\right)\left(x-5\right)+\left(x+3\right)\left(3x-4\right)=0\)
=>(x+3)(x-5+3x-4)=0
=>(x+3)(4x-9)=0
=>\(\left[{}\begin{matrix}x=-3\\x=\dfrac{9}{4}\end{matrix}\right.\)
f: \(\left(x+7\right)\left(3x-1\right)=49-x^2\)
=>\(\left(x+7\right)\left(3x-1\right)+x^2-49=0\)
=>(x+7)(3x-1)+(x-7)(x+7)=0
=>(x+7)(3x-1+x-7)=0
=>(x+7)(4x-8)=0
=>\(\left[{}\begin{matrix}x=-7\\x=2\end{matrix}\right.\)
g: \(3x^2-7x+4=0\)
=>\(3x^2-3x-4x+4=0\)
=>(x-1)(3x-4)=0
=>\(\left[{}\begin{matrix}x=1\\x=\dfrac{4}{3}\end{matrix}\right.\)
h: \(2x^3+3x^2-32x=48\)
=>\(2x^3+3x^2-32x-48=0\)
=>\(x^2\left(2x+3\right)-16\left(2x+3\right)=0\)
=>\(\left(2x+3\right)\left(x^2-16\right)=0\)
=>(2x+3)(x-4)(x+4)=0
=>\(\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=4\\x=-4\end{matrix}\right.\)
a) (x + 5)(x - 1) = 2x(x - 1)
(x + 5)(x - 1) - 2x(x - 1) = 0
(x - 1)(x + 5 - 2x) = 0
(x - 1)(5 - x) = 0
x - 1 = 0 hoặc 5 - x = 0
*) x - 1 = 0
x = 1
*) 5 - x = 0
x = 5
Vậy S = {1; 5}
b) 3(x - 1)(2x - 1) = 5(x + 8)(x - 1)
(x - 1)(6x - 3) = (5x + 40)(x - 1)
(x - 1)(6x - 3) - (5x + 40)(x - 1) = 0
(x - 1)(6x - 3 - 5x - 40) = 0
(x - 1)(x - 43) = 0
x - 1 = 0 hoặc x - 43 = 0
*) x - 1 = 0
x = 1
*) x - 43 = 0
x = 43
Vậy S = {1; 43}
c) (x² - 5x + 7)² - (2x - 5)² = 0
(x² - 5x + 7 - 2x + 5)(x² - 5x + 7 + 2x - 5) = 0
(x² - 7x + 12)(x² - 3x + 2) = 0
x² - 7x + 12 = 0 hoặc x² - 3x + 2 = 0
*) x² - 7x + 12 = 0
x² - 3x - 4x + 12 = 0
(x² - 3x) - (4x + 12) = 0
x(x - 3) - 4(x - 3) = 0
(x - 3)(x - 4) = 0
x - 3 = 0 hoặc x - 4 = 0
+) x - 3 = 0
x = 3
+) x - 4 = 0
x = 4
*) x² - 3x + 2 = 0
x² - x - 2x + 2 = 0
(x² - x) - (2x - 2) = 0
x(x - 1) - 2(x - 1) = 0
(x - 1)(x - 2) = 0
x - 1 = 0 hoặc x - 2 = 0
+) x - 1 = 0
x = 1
+) x - 2 = 0
x = 2
Vậy S = {1; 2; 3; 4}
d) x³ - 5x² + 6x = 0
x(x² - 5x + 6) = 0
x = 0 hoặc x² - 5x + 6 = 0
*) x² - 5x + 6 = 0
x² - 2x - 3x + 6 = 0
(x² - 2x) - (3x - 6) = 0
x(x - 2) - 3(x - 2) = 0
(x - 2)(x - 3) = 0
x - 2 = 0 hoặc x - 3 = 0
+) x - 2 = 0
x = 2
+) x - 3 = 0
x = 3
Vậy S = {0; 2; 3}