Cho biểu thức $A=\Big(\dfrac{4\sqrt{x}}{2+\sqrt{x}}+\dfrac{8x}{4-x}\Big) \, : \, \Big(\dfrac{\sqrt{x}-1}{x-2\sqrt{x}}-\dfrac{2}{\sqrt{x}}\Big)$ với $x>0; \, x\ne 4; \, x\ne 9$.
a) Rút gọn biểu thức $A$.
b) Tìm $x$ để $A = - 2$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(Q=\dfrac{\sqrt{x^3}-\sqrt{x}+2x-2}{\sqrt{x}+2}\)
\(=\dfrac{x\sqrt{x}-\sqrt{x}+2\left(x-1\right)}{\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}\left(x-1\right)+2\left(x-1\right)}{\sqrt{x}+2}=\dfrac{\left(x-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}=x-1\)
\(P=\dfrac{2x-3\sqrt{x}-2}{\sqrt{x}-2}\)
\(=\dfrac{2x-4\sqrt{x}+\sqrt{x}-2}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)+\left(\sqrt{x}-2\right)}{\sqrt{x}-2}=2\sqrt{x}+1\)
b: P=Q
=>\(x-1=2\sqrt{x}+1\)
=>\(x-2\sqrt{x}-2=0\)
=>\(x-2\sqrt{x}+1=3\)
=>\(\left(\sqrt{x}-1\right)^2=3\)
mà \(\sqrt{x}-1>=-1\) với mọi x thỏa mãn ĐKXĐ
nên \(\sqrt{x}-1=\sqrt{3}\)
=>\(\sqrt{x}=1+\sqrt{3}\)
=>\(x=\left(1+\sqrt{3}\right)^2=4+2\sqrt{3}\left(nhận\right)\)

a: \(P=\dfrac{3}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-5}{x-1}\)
\(=\dfrac{3}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\left(\sqrt{x}-1\right)-\sqrt{x}-1-\sqrt{x}+5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}-3-2\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{1}{\sqrt{x}-1}\)
b: \(x=24-16\sqrt{2}=8\left(3-2\sqrt{2}\right)=8\left(\sqrt{2}-1\right)^2\)
Thay \(x=8\left(\sqrt{2}-1\right)^2\) vào P, ta được:
\(P=\dfrac{1}{\sqrt{8\left(\sqrt{2}-1\right)^2}-1}\)
\(=\dfrac{1}{2\sqrt{2}\left(\sqrt{2}-1\right)-1}=\dfrac{1}{4-2\sqrt{2}-1}\)
\(=\dfrac{1}{3-2\sqrt{2}}=3+2\sqrt{2}\)

ĐKXĐ: x>=0; x<>4
a: Thay x=9 vào A, ta được:
\(A=\dfrac{3}{3-2}=\dfrac{3}{1}=3\)
b: T=A-B
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{x-4}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)-2\left(\sqrt{x}-2\right)-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+2\sqrt{x}-2\sqrt{x}+4-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
c: Để T nguyên thì \(\sqrt{x}-2⋮\sqrt{x}+2\)
=>\(\sqrt{x}+2-4⋮\sqrt{x}+2\)
=>\(-4⋮\sqrt{x}+2\)
mà \(\sqrt{x}+2>=2\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}+2\in\left\{2;4\right\}\)
=>\(x\in\left\{0;4\right\}\)
Kết hợp ĐKXĐ, ta được: x=0

a: Thay x=9 vào P, ta được:
\(P=\dfrac{9+3}{\sqrt{9}-2}=\dfrac{12}{3-2}=\dfrac{12}{1}=12\)
b: \(Q=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}+\dfrac{5\sqrt{x}-2}{x-4}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}+\dfrac{5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
c: Đặt A=P:Q
\(=\dfrac{x+3}{\sqrt{x}-2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{x+3}{\sqrt{x}}=\sqrt{x}+\dfrac{3}{\sqrt{x}}>=2\cdot\sqrt{\sqrt{x}\cdot\dfrac{3}{\sqrt{x}}}=2\sqrt{3}\) với mọi x thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\left(\sqrt{x}\right)^2=3\)
=>x=3(nhận)

a: \(P=\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\left(\dfrac{x-2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\cdot\sqrt{x}}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
b: \(2P=2\sqrt{x}+5\)
=>\(2\left(\sqrt{x}+1\right)=\sqrt{x}\left(2\sqrt{x}+5\right)\)
=>\(2x+5\sqrt{x}-2\sqrt{x}-2=0\)
=>\(2x+3\sqrt{x}-2=0\)
=>\(\left(\sqrt{x}+2\right)\left(2\sqrt{x}-1\right)=0\)
mà \(\sqrt{x}+2>=2>0\forall x\) thỏa mãn ĐKXĐ
nên \(2\sqrt{x}-1=0\)
=>\(\sqrt{x}=\dfrac{1}{2}\)
=>\(x=\dfrac{1}{4}\left(nhận\right)\)

ĐKXĐ: x>0; x<>9
a:\(P=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{3}{x\sqrt{x}-9\sqrt{x}}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{3\sqrt{x}-3}{x+3\sqrt{x}}\right)\)
\(=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{3}{\sqrt{x}\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{3\sqrt{x}-3}{\sqrt{x}\left(\sqrt{x}+3\right)}\right)\)
\(=\dfrac{x-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\cdot\sqrt{x}}:\dfrac{x-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\cdot\sqrt{x}}\)
\(=\dfrac{x-3\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x-3\sqrt{x}+3}=\dfrac{1}{\sqrt{x}-3}\)
b: P>1
=>P-1>0
=>\(\dfrac{1-\sqrt{x}+3}{\sqrt{x}-3}>0\)
=>\(\dfrac{4-\sqrt{x}}{\sqrt{x}-3}>0\)
=>\(\dfrac{\sqrt{x}-4}{\sqrt{x}-3}< 0\)
=>\(3< \sqrt{x}< 4\)
=>9<x<16

a: \(P=\left(\dfrac{2\sqrt{xy}}{x-y}-\dfrac{\sqrt{x}+\sqrt{y}}{2\sqrt{x}-2\sqrt{y}}\right)\cdot\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
\(=\left(\dfrac{2\sqrt{xy}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}-\dfrac{\sqrt{x}+\sqrt{y}}{2\left(\sqrt{x}-\sqrt{y}\right)}\right)\cdot\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
\(=\dfrac{4\sqrt{xy}-\left(\sqrt{x}+\sqrt{y}\right)^2}{2\cdot\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\cdot\dfrac{2\sqrt{x}}{\left(\sqrt{x}-\sqrt{y}\right)}\)
\(=\dfrac{-x+2\sqrt{xy}-y}{\left(\sqrt{x}-\sqrt{y}\right)^2}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}=\dfrac{-\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)^2}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)
\(=-\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)
b: \(\dfrac{x}{y}=\dfrac{4}{9}\)
=>\(\dfrac{x}{4}=\dfrac{y}{9}=k\)
=>x=4k; y=9k
\(P=\dfrac{-\sqrt{x}}{\sqrt{x}+\sqrt{y}}=\dfrac{-\sqrt{4k}}{\sqrt{4k}+\sqrt{9k}}=\dfrac{-2\sqrt{k}}{2\sqrt{k}+3\sqrt{k}}=-\dfrac{2}{5}\)

a) Gọi x là số đo cung nhỏ AB (x > 0)
Số đo cung lớn AB là 3x
Ta có:
x + 3x = 360⁰
4x = 360⁰
x = 360⁰ : 4
x = 90⁰
Vậy số đo cung nhỏ AB là 90⁰
Số đo cung lớn AB là 3.90⁰ = 270⁰
b)
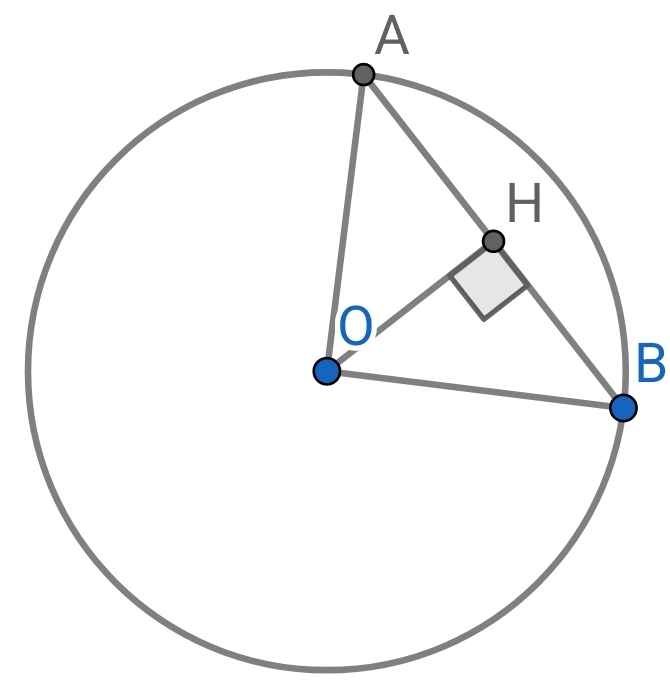
Do số đo cung nhỏ AB là 90⁰ (cmt)
⇒ ∠AOB = 90⁰
⇒ ∆AOB vuông tại O
Do OH là khoảng cách từ O đến AB
⇒ OH ⊥ AB
⇒ H là trung điểm của AB
⇒ OH là đường trung tuyến ứng với cạnh huyền AB của ∆AOB vuông tại O
⇒ OH = AB : 2

Gọi x là số đo cung nhỏ AB (x > 0)
Số đo cung lớn AB là 2x
Ta có:
x + 2x = 360⁰
3x = 360⁰
x = 360⁰ : 3
x = 120⁰
⇒ ∠AOB = 120⁰
∆AOB có:
OA = OB = R
⇒ ∆AOB cân tại O
⇒ ∠OAB = ∠OBA = (180⁰ - ∠AOB) : 2
= (180⁰ - 120⁰) : 2
= 30⁰
Ta có hình vẽ sau:
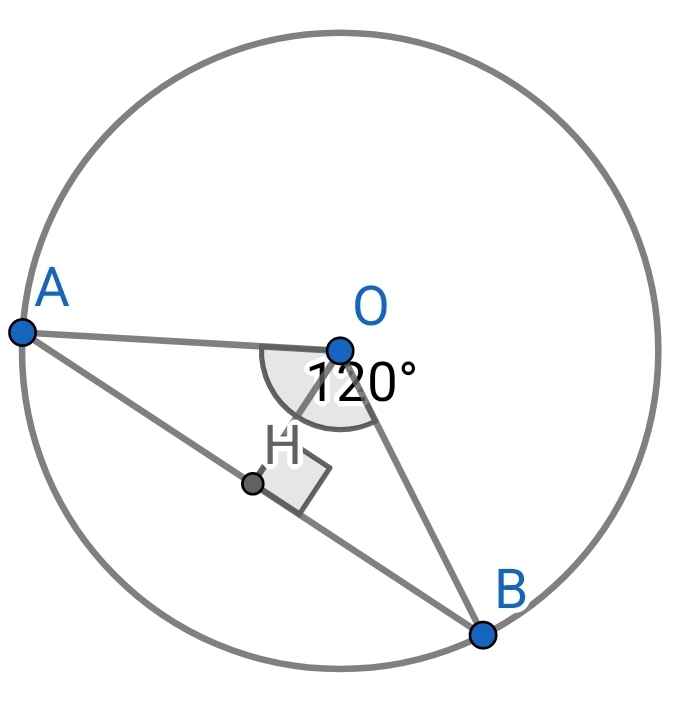
Vẽ đường cao OH của ∆OAB
⇒ ∆OAH vuông tại H
⇒ cosOAH = AH : OA
⇒ AH = OA.cosOAH
= R.cos30⁰

Do OH ⊥ AB
⇒ H là trung điểm của AB
⇒ AB = 2AH
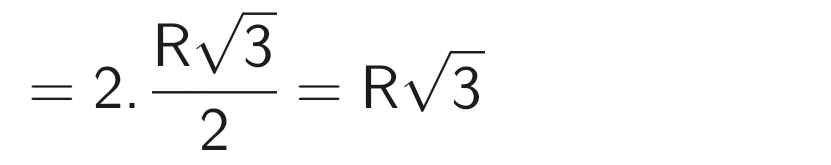
a: \(A=\left(\dfrac{4\sqrt{x}}{\sqrt{x}+2}+\dfrac{8x}{4-x}\right):\left(\dfrac{\sqrt{x}-1}{x-2\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\)
\(=\left(\dfrac{4\sqrt{x}}{\sqrt{x}+2}-\dfrac{8x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-2\right)}-\dfrac{2}{\sqrt{x}}\right)\)
\(=\dfrac{4\sqrt{x}\left(\sqrt{x}-2\right)-8x}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}:\dfrac{\sqrt{x}-1-2\left(\sqrt{x}-2\right)}{\sqrt[]{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4x-8\sqrt{x}-8x}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}-1-2\sqrt{x}+4}\)
\(=\dfrac{-4x-8\sqrt{x}}{\sqrt{x}+2}\cdot\dfrac{\sqrt{x}}{-\sqrt{x}+3}=\dfrac{-4\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)}\cdot\dfrac{-\sqrt{x}}{\sqrt{x}-3}\)
\(=\dfrac{4x}{\sqrt{x}-3}\)
b: A=-2
=>\(4x=-2\left(\sqrt{x}-3\right)=-2\sqrt{x}+6\)
=>\(4x+2\sqrt{x}-6=0\)
=>\(2x+\sqrt{x}-3=0\)
=>\(\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)=0\)
mà \(2\sqrt{x}+3>=3>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}-1=0\)
=>x=1(nhận)