Cho tam giác ABC vuông tại A có AB < AC đường cao AH . Gọi D là hình chiếu của H trên AB , E là hình chiếu của H trên AC Chứng minh rằng AD x AB + AE x AC = 2 x DE^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne4\end{matrix}\right.\)
\(P=\left(\dfrac{2}{x-4}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{1}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Để P=3/2 thì \(\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{3}{2}\)
=>\(3\left(\sqrt{x}-2\right)=2\sqrt{x}\)
=>\(3\sqrt{x}-2\sqrt{x}=6\)
=>\(\sqrt{x}=6\)
=>x=36(nhận)

a: 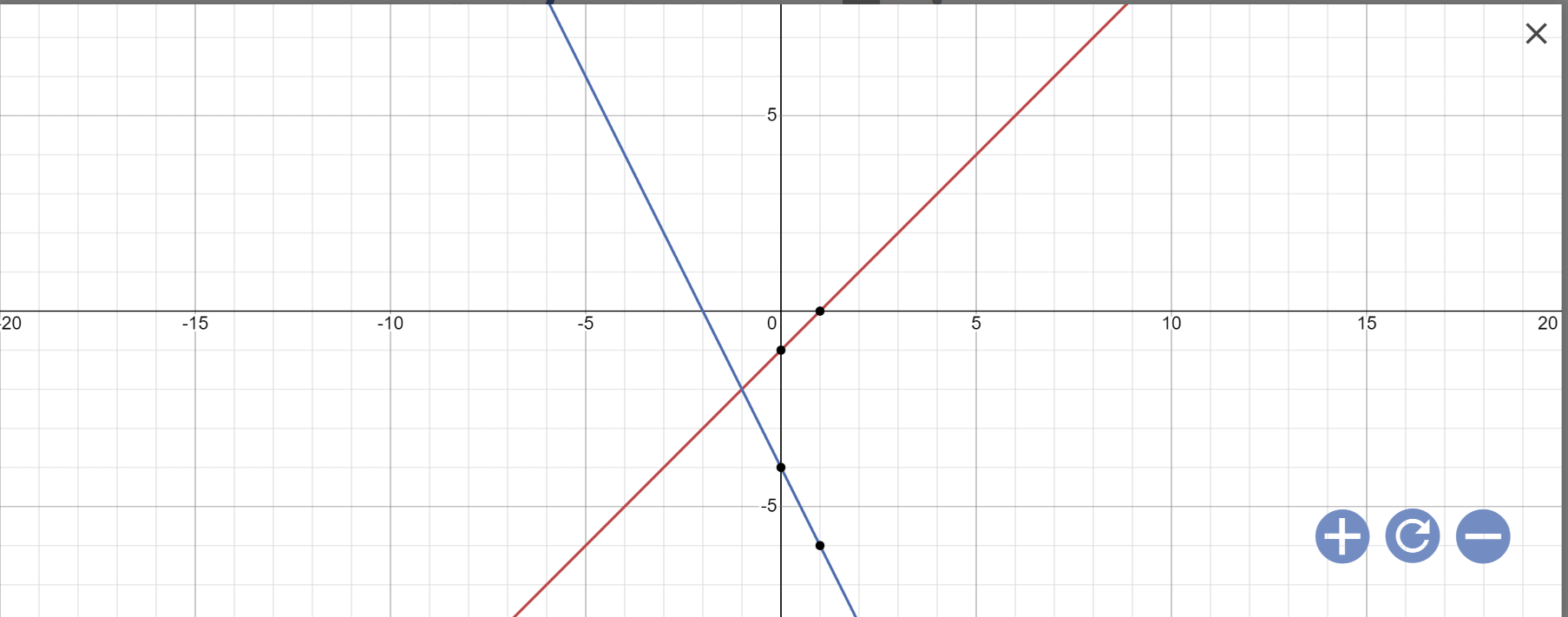
b: Phương trình hoành độ giao điểm là:
-2x-4=x-1
=>-2x-x=-1+4
=>-3x=3
=>x=-1
Thay x=-1 vào y=x-1, ta được:
y=-1-1=-2
Vậy: Tọa độ giao điểm là A(-1;-2)

Để hệ có nghiệm duy nhất thì \(\dfrac{a+1}{1}\ne\dfrac{-a}{a}=-1\)
=>\(a+1\ne-1\)
=>\(a\ne-2\)
\(\left\{{}\begin{matrix}\left(a+1\right)x-ay=5\\x+ay=a^2+4a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)x-ay+x+ay=5+a^2+4a\\x+ay=a^2+4a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(a+2\right)=a^2+4a+5\\ay=a^2+4a-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\ay=a^2+4a-\dfrac{a^2+4a+5}{a+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\ay=\dfrac{\left(a+2\right)\left(a^2+4a\right)-a^2-4a-5}{a+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{a^2+4a+5}{a+2}\\y=\dfrac{a^3+4a^2+2a^2+8a-a^2-4a-5}{a\left(a+2\right)}=\dfrac{a^3+5a^2+4a-5}{a\left(a+2\right)}\end{matrix}\right.\)
Để x,y nguyên thì \(\left\{{}\begin{matrix}a^2+4a+5⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a^2+4a+4+1⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1⋮a+2\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a+2\in\left\{1;-1\right\}\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a\in\left\{-1;-3\right\}\\a^3+5a^2+4a-5⋮a^2+2a\end{matrix}\right.\Leftrightarrow a=-1\)

sin a=0,3
=>\(a=arcsin\left(0,3\right)\simeq17^0\)
cos a=0,45
=>\(a=arccos\left(0,45\right)\simeq63^0\)
\(tana=2,5\)
=>\(a=arctan\left(2,5\right)\simeq68^0\)

Dựng \(BH\perp AC\left(H\in AC\right)\)
Xét tg vuông BHC có
\(BC^2=BH^2+CH^2\) (Pitago)
\(\Rightarrow a^2=BH^2+\left(AC-AH\right)^2=BH^2+AC^2+AH^2-2AC.AH=\)
\(=\left(BH^2+AH^2\right)+AC^2-2AC.AH\) (1)
Xét tg vuông AHB có
\(BH^2+AH^2=AB^2=c^2\)
\(AH=AB\cos A=c\cos A\)
Thay vào (1)
\(\Rightarrow a^2=b^2+c^2-2bc\cos A\)

Gọi số học sinh nam của lớp đó là `a` (học sinh)
Số học sinh nữ của lớp đó là `b` (học sinh)
ĐK: `0<a,b<43` và `a,b∈N`
Số học sinh nam hơn số học sinh nữ là 3 hs nên ta có pt:
`a-b=3(1)`
Số học sinh của lớp là 43 học sinh nên ta có pt:
`a+b=43(2) `
Từ (1) và (2) ta có hpt: \(\left\{{}\begin{matrix}a-b=3\\a+b=43\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=46\\b=a-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=23\\b=23-3=20\end{matrix}\right.\left(tm\right)\)
Vậy: ...


Em để ý thấy 2 số hạng đầu nếu đặt \(x\sqrt{x}\) làm nhân tử chung được: \(x\sqrt{x}\left(\sqrt{x}+1\right)\)
Giờ nó lại xuất hiện nhân tử \(\sqrt{x}+1\) với 2 số hạng cuối
Cứ vậy là ra thôi

a.
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3y\right)\left(2x-y\right)=0\\6x^2+7xy-5y^2=0\end{matrix}\right.\)
TH1: \(2x-3y=0\Rightarrow y=\dfrac{2}{3}x\) thay vào pt dưới
\(\Rightarrow6x^2+7x.\left(\dfrac{2}{3}x\right)-5\left(\dfrac{2}{3}x\right)^2=0\)
\(\Leftrightarrow\dfrac{76}{9}x^2=0\Rightarrow x=0\Rightarrow y=0\)
TH2: \(2x-y=0\Rightarrow y=2x\)
Tương tự ta cũng được \(x=0;y=0\)
Vậy hệ có nghiệm duy nhất \(\left(x;y\right)=\left(0;0\right)\)
b.
\(\Leftrightarrow\left\{{}\begin{matrix}13x^2-39xy+13y^2=-13\\2x^2+xy+3y^2=13\end{matrix}\right.\)
Cộng vế với vế
\(\Rightarrow15x^2-38xy+16y^2=0\)
\(\Leftrightarrow\left(x-2y\right)\left(15x-8y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2y\\x=\dfrac{8}{15}y\end{matrix}\right.\)
Thay vào pt đầu:
- Với \(x=2y\Rightarrow4y^2-6y^2+y^2=-1\)
\(\Rightarrow y^2=1\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-1\Rightarrow x=-2\end{matrix}\right.\)
- Với \(x=\dfrac{8}{15}y\)
\(\Rightarrow\left(\dfrac{8}{15}y\right)^2-3\left(\dfrac{8}{15}y\right).y+y^2=-1\)
\(\Leftrightarrow-\dfrac{71}{225}y^2=-1\Rightarrow y^2=\dfrac{225}{71}\)
\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{15}{\sqrt{71}}\Rightarrow x=\dfrac{8}{\sqrt{71}}\\y=-\dfrac{15}{\sqrt{71}}\Rightarrow x=-\dfrac{8}{\sqrt{71}}\end{matrix}\right.\)

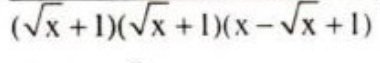
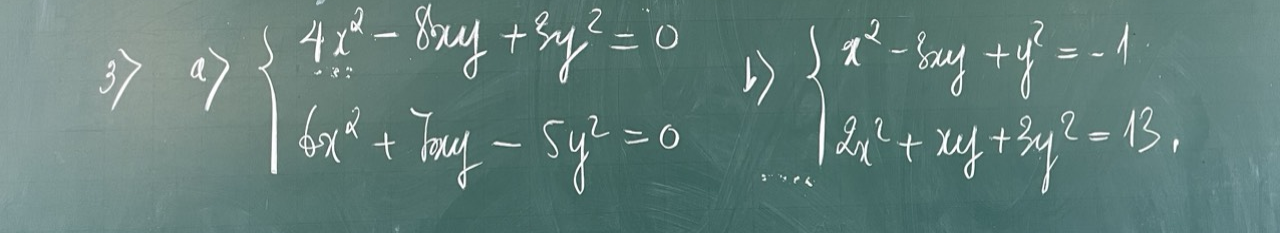
Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>AH=DE
Xét ΔABH vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\)
\(AD\cdot AB+AE\cdot AC=AH^2+AH^2\)
\(=2AH^2=2DE^2\)