cho tam giác ABC cân tại B có đường p/g BD cắt đường trung tuyến AM tại G. a) C/M tam giác BAG=tam giác BCH và tam giác AGC cân. b) C/M BG là đường trung trực đoạn thẳng AC. c) qua C kẻ đường thẳng vuông góc của AC đường thẳng này cắt AM kéo dài tại E,C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(Q=\left(x-y\right)^2-\left(x-y\right)\left(x+y\right)+\left(x-2y\right)^2\)
\(=\left(x-y\right)\left(x-y-x-y\right)+\left(x-2y\right)^2\)
\(=-2y\left(x-y\right)+x^2-4xy+4y^2\)
\(=-2xy+2y^2+x^2-4xy+4y^2\)
\(=x^2-6xy+6y^2\)
b: \(\left(3x-1\right)^2-\left(x+7\right)^2-\left(2x-5\right)\left(2x+5\right)\)
\(=9x^2-6x+1-x^2-14x-49-\left(4x^2-25\right)\)
\(=8x^2-20x-48-4x^2+25=4x^2-20x-23\)

\(a,y^2+2y+1=y^2+2.y.1+1^2=\left(y+1\right)^2\)
\(b,9x^2+y^2-6xy=\left(3x\right)^2-2\cdot3x\cdot y+y^2=\left(3x-y\right)^2\)
\(c,25a^2+4b^2+20ab=\left(5a\right)^2+2\cdot5a\cdot2b+\left(2b\right)^2=\left(5a+2b\right)^2\)
\(d,x^2-x+\dfrac{1}{4}=x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2=\left(x-\dfrac{1}{2}\right)^2\)
`y^2 + 2y + 1 = y^2 + 2y .1 + 1^2 + (y+1)^2`
`9x^2 + y^2 - 6xy = (3x)^2 - 2.3x.y + y^2 = (3x + y)^2`
`25a^2 + 4b^2 + 20ab = (5a)^2 + 2.5a .2b + (2b)^2 = (5a + 2b)^2`
`x^2 - x + 1/4 = x^2 - 2x .1/2 +(1/2)^2 = (x-1/2)^2`

a: \(\dfrac{x-x^2}{5x^2-5}=\dfrac{x}{M}\)
=>\(M=\dfrac{x\left(5x^2-5\right)}{-x^2+x}=\dfrac{5x\left(x-1\right)\left(x+1\right)}{-x\left(x-1\right)}=-5\left(x+1\right)\)
=>M=-5x-5
b: \(\dfrac{x^2+8}{2x-1}=\dfrac{3x^3+24x}{M}\)
=>\(M=\dfrac{\left(2x-1\right)\left(3x^3+24x\right)}{x^2+8}=\dfrac{\left(2x-1\right)\cdot3x\left(x^2+8\right)}{\left(x^2+8\right)}\)
=>\(M=3x\left(2x-1\right)=6x^2-3x\)
c: \(\dfrac{M}{x-y}=\dfrac{3x^2-3xy}{3\left(y-x\right)^2}\)
=>\(\dfrac{M}{x-y}=\dfrac{3x\left(x-y\right)}{3\left(x-y\right)^2}=\dfrac{x}{x-y}\)
=>M=x

\(x^4+8x=0\)
=>\(x\left(x^3+8\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x^3+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(x^4\) + 8\(x\) = 0
\(x^{ }\)(\(x^3\) + 8) = 0
\(\left[{}\begin{matrix}x=0\\x^3+8=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x^3=-8\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-2; 0}

ΔAED vuông tại A
=>\(AE^2+AD^2=ED^2\)
ΔAEB vuông tại A
=>\(AE^2+AB^2=EB^2\)
ΔACD vuông tại A
=>\(AC^2+AD^2=CD^2\)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
\(CD^2-CB^2=CA^2+AD^2-CA^2-AB^2=AD^2-AB^2\)
\(ED^2-EB^2=AE^2+AD^2-AE^2-AB^2=AD^2-AB^2\)
Do đó: \(CD^2-CB^2=ED^2-EB^2\)

Gọi vận tốc xe máy là x(km/h)
(Điều kiện: x>28)
Vận tốc của người đi xe đạp là x-28(km/h)
Tổng vận tốc của hai xe là 156:3=52(km/h)
=>x+x-28=52
=>2x=80
=>x=40(nhận)
Vậy: Vận tốc xe máy là 40km/h
Vận tốc của người đi xe đạp là 40-28=12km/h

Gọi vận tốc ban đầu của ô tô là x(km/h)
(Điều kiện: x>0)
Thời gian ô tô đi 180km đầu tiên là: \(\dfrac{180}{x}\left(giờ\right)\)
Độ dài quãng đường còn lại là 400-180=220(km)
Vận tốc của ô tô khi đi trên quãng đường còn lại là:
x+10(km/h)
Thời gian ô tô đi 220km còn lại là \(\dfrac{220}{x+10}\left(giờ\right)\)
Thời gian đi hết quãng đường là 8 giờ nên ta có:
\(\dfrac{180}{x}+\dfrac{220}{x+10}=8\)
=>\(\dfrac{45}{x}+\dfrac{55}{x+10}=2\)
=>\(\dfrac{45x+450+55x}{x\left(x+10\right)}=2\)
=>2x(x+10)=100x+450
=>x(x+10)=50x+225
=>\(x^2-40x-225=0\)
=>(x-45)(x+5)=0
=>\(\left[{}\begin{matrix}x=45\left(nhận\right)\\x=-5\left(loại\right)\end{matrix}\right.\)
Vậy: vận tốc ban đầu của ô tô là 45km/h
Giải:
Gọi vận tốc ban đầu của ô tô là: \(x\) (km/h) ; \(x\) > 0
Vận tốc lúc sau của ô tô là: \(x+10\) (km/h)
Thời gian ô tô đi lúc đầu là: 180 : \(x\) (giờ)
Thời gian ô tô đi lúc sau là: (400 - 180) : (\(x+10\)) = \(\dfrac{220}{x+10}\)
Theo bài ra ta có phương trình:
\(\dfrac{180}{x}\) + \(\dfrac{220}{x+10}\) = 8
\(\dfrac{45}{x}\) + \(\dfrac{55}{x+10}\) = 2
45(\(x+10\)) + 55\(x\) = 2.\(x\) (\(x+10\))
45\(x\) + 450 + 55\(x\) = 2\(x^2\) + 20\(x\)
2\(x^2\) + 20\(x\) - 55\(x\) - 45\(x\) = 450
2\(x^2\) + (20\(x\) - 55\(x\) - 45\(x\)) = 450
2\(x^2\) + (- 35\(x\) - 45\(x\)) = 450
2\(x^2\) - 80\(x\) = 450
\(x^2\) - 40\(x\) = 225
\(x^2\) - 40\(x\) + 400 = 625
(\(x-20\))2 = 252
\(\left[{}\begin{matrix}x-20=25\\x-20=-25\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=25+20\\x=-25+20\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=45\\x=-5\end{matrix}\right.\)
\(x=-5\) < 0 (loại)
Vậy \(x=45\)
Kết luận:...
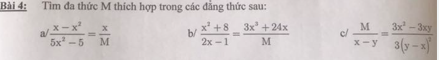
a: Xét ΔBAG và ΔBCG có
BA=BC
\(\widehat{ABG}=\widehat{CBG}\)
BG chung
Do đó: ΔBAG=ΔBCG
=>GA=GC
=>ΔGAC cân tại G
b: Ta có: BA=BC
=>B nằm trên đường trung trực của AC(1)
Ta có: GA=GC
=>G nằm trên đường trung trực của AC(2)
Từ (1),(2) suy ra BG là đường trung trực của AC