tìm nghiệm của đa thức a= (x+1^2022)+2024
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC
AM chung
Do đó: ΔAMB=ΔAMC
b: ΔAMB=ΔAMC
=>MB=MC
=>M là trung điểm của BC
Xét ΔGBC có
GM là đường cao
GM là đường trung tuyến
Do đó; ΔGBC cân tại G
c: Sửa đề: Trên tia đối của tia FB lấy H sao cho FG=FH
Xét ΔABC có
AM,BF là các đường trung tuyến
AM cắt BF tại G
Do đó: G là trọng tâm của ΔABC
=>BG=2GF
mà GH=2GF(F là trung điểm của GH)
nên BG=GH
=>G là trung điểm của BH
Xét ΔHBC có
G là trung điểm của HB
GI//BC
Do đó: I là trung điểm của HC
Xét ΔHGC có
CF,GI là các đường trung tuyến
CF cắt GI tại K
Do đó: K là trọng tâm của ΔHGC

Sửa đề: Vuông góc BC tại E
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Sửa đề: ED cắt AB tại F, chứng minh ΔDFC cân
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D
c: Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE và AF=EC
nên BF=BC
ΔBFC cân tại B
mà BH là đường phân giác
nên H là trung điểm của FC
d: Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE

a: Kẻ DM//AC
=>\(\widehat{DMB}=\widehat{ACB}\)
=>\(\widehat{DMB}=\widehat{DBM}\)
=>DM=DB
mà DB=CE
nên DM=CE
Xét ΔIMD và ΔIEC có
\(\widehat{IMD}=\widehat{ICE}\)(MD//CE)
DM=CE
\(\widehat{IDM}=\widehat{ICE}\)(DM//CE)
Do đó: ΔIMD=ΔIEC
=>ID=IE
=>I là trung điểm của DE
b: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
Xét ΔABO và ΔACO có
AB=AC
\(\widehat{BAO}=\widehat{CAO}\)
AO chung
Do đó: ΔABO=ΔACO
=>OB=OC và \(\widehat{ABO}=\widehat{ACO}=90^0\)
Xét ΔOBD vuông tại B và ΔOCE vuông tại C có
OB=OC
BD=CE
Do đó: ΔOBD=ΔOCE
=>OD=OE
ΔODE cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)DE

a.
\(M\left(x\right)=2x^5+5x^4-7x^3-2x^2-\dfrac{1}{4}x\)
\(\Rightarrow M\left(x\right)\) có bậc 5
\(N\left(x\right)=-2x^5+3x^4-2x^3+7x^2-\dfrac{1}{4}\)
\(\Rightarrow N\left(x\right)\) có bậc 5
b.
\(M\left(x\right)+N\left(x\right)=8x^4-9x^3+5x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)

Bài 1:
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>BH=CK
Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
=>\(\widehat{IBC}=\widehat{ICB}\)
=>IB=IC
=>I nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AI là đường trung trực của BC
Bài 3:
a: Xét ΔHEB vuông tại E và ΔHFC vuông tại F có
HB=HC
\(\widehat{HBE}=\widehat{HCF}\)
Do đó; ΔHEB=ΔHFC
b: Xét ΔAMK có
MF,KE là các đường cao
MF cắt KE tại H
Do đó: H là trực tâm của ΔAMK
=>AH\(\perp\)MK


Gọi số quyển tập ba lớp 7A,7B,7C quyên góp được lần lượt là a(quyển),b(quyển),c(quyển)
(Điều kiện: \(a,b,c\in Z^+\))
Số quyển tập ba lớp quyên góp được lần lượt tỉ lệ với 7;3;4 nên \(\dfrac{a}{7}=\dfrac{b}{3}=\dfrac{c}{4}\)
Tổng số quyển tập ba lớp quyên góp được là 420 nên a+b+c=420
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{7}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{7+3+4}=\dfrac{420}{14}=30\)
=>\(a=30\cdot7=210\left(nhận\right);b=3\cdot30=90\left(nhận\right);c=4\cdot30=120\left(nhận\right)\)
vậy: số quyển tập ba lớp 7A,7B,7C quyên góp được lần lượt là 210(quyển),90(quyển),120(quyển)

Gọi số tiền đơn vị 1,2,3 đóng góp lần lượt là a(triệu),b(triệu),c(triệu)
(Điều kiện: a>0; b>0; c>0)
Số tiền đóng góp của 3 đơn vị lần lượt tỉ lệ với 3;5;8 nên \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\)
Tổng số tiền lãi là 256 triệu nên a+b+c=256
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}=\dfrac{a+b+c}{3+5+8}=\dfrac{256}{16}=16\)
=>\(a=16\cdot3=48;b=16\cdot5=80;c=16\cdot8=128\)
vậy: Số tiền ba đơn vị đóng góp lần lượt là 48 triệu; 80 triệu; 128 triệu

\(4x^2+4x=2\)
=>\(2x^2+2x=1\)
=>\(2x^2+2x-1=0\)
\(\Delta=2^2-4\cdot2\cdot\left(-1\right)=4+8=12>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-2-\sqrt{12}}{2\cdot2}=\dfrac{-2-2\sqrt{3}}{4}=\dfrac{-1-\sqrt{3}}{2}\\x_2=\dfrac{-1+\sqrt{3}}{2}\end{matrix}\right.\)
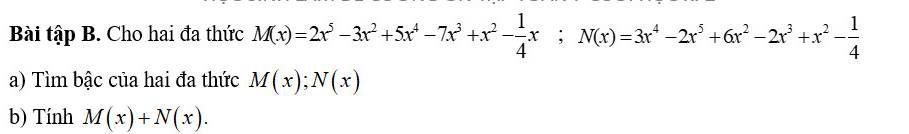

a=(x+1^2022)+2024=0
. x+1^2022=2024
x+1=2024
x=2023
Vậy đa thức a có nghiệm là x=2023