vì góc A và góc B là 2 góc bù nhau nên

góc A + góc B = 180 độ (1)

mà góc A = 1/6B (2)

từ (1) (2) => 1/6B + B = 180

7/6B = 180

B = 154 độ

A = 180 - 154 = 26

vậy góc A = 26 độ

Lúc đầu anh trai nhiều hơn em trai số quả bóng là:

      13 + 13 = 26 (quả)

       Đ/s: 26 quả bóng

gọi số bóng ban đầu của anh là x; số bóng ban đầu của em là y

ta có: x - 13 = y + 13

x - y = 13 + 13

x - y = 26

vậy lúc đầu anh nhiều hơn em 26 quả bóng

a: \(\dfrac{8}{9}=1-\dfrac{1}{9}\)

\(\dfrac{108}{109}=1-\dfrac{1}{109}\)

Vì 9<109 nên \(\dfrac{1}{9}>\dfrac{1}{109}\)

=>\(-\dfrac{1}{9}< -\dfrac{1}{109}\)

=>\(-\dfrac{1}{9}+1< -\dfrac{1}{109}+1\)

=>\(\dfrac{8}{9}< \dfrac{108}{109}\)

b: \(\dfrac{97}{100}=0,97;\dfrac{98}{99}=0,\left(98\right)\)

mà 0,97<0,(98)

nên \(\dfrac{97}{100}< \dfrac{98}{99}\)

c: \(\dfrac{19}{18}=1+\dfrac{1}{18}\)

\(\dfrac{2021}{2020}=1+\dfrac{1}{2020}\)

Vì 18<2020 nên \(\dfrac{1}{18}>\dfrac{1}{2020}\)

=>\(1+\dfrac{1}{18}>1+\dfrac{1}{2020}\)

=>\(\dfrac{19}{18}>\dfrac{2021}{2020}\)

d: \(\dfrac{131}{171}=\dfrac{130+1}{170+1}>\dfrac{130}{170}=\dfrac{13}{17}\)

Đề thiếu rồi bạn. Cho a và b thỏa mãn biểu thức đó như thế nào?

Bài 1:

a; \(\dfrac{1}{n}\); \(\dfrac{1}{n+1}\) (n > 0; n \(\in\) Z) 

  \(\dfrac{1}{n}\) - \(\dfrac{1}{n+1}\) = \(\dfrac{n+1-1}{n.\left(n+1\right)}\) = \(\dfrac{1}{n\cdot\left(n+1\right)}\) 

⇒ \(\dfrac{1}{n}\) - \(\dfrac{1}{n+1}\) = \(\dfrac{1}{n\left(n+1\right)}\) (đpcm)

Bài 1b

A = \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\) + \(\dfrac{1}{7.8}\) + \(\dfrac{1}{8.9}\)

A =  \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) +\(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{8}\) + \(\dfrac{1}{8}\) - \(\dfrac{1}{9}\)

A =    \(\dfrac{1}{2}\) - \(\dfrac{1}{9}\)

A =    \(\dfrac{7}{18}\) 

Gọi số nhãn vở của Chi là x(nhãn)

(Điều kiện: \(x\in Z^+\))

Trung bình cộng số nhãn vở của 3 bạn là \(\dfrac{x+20+20}{3}=\dfrac{x+40}{3}\)

Chi có số nhãn vở ít hơn trung bình cộng của 3 bạn là 6 cái nên ta có:

\(\dfrac{x+40}{3}-x=6\)

=>\(\dfrac{x+40-3x}{3}=6\)

=>-2x+40=18

=>-2x=-22

=>x=11(nhận)

Vậy: Chi có 11 nhãn vở

Gọi số nhãn vở của Chi là \(x\) (nhãn) (\(x\inℕ^∗\))

Ta có: Trung bình cộng số nhãn vở của 3 bạn là:

\(\dfrac{x+20+20}{3}=\dfrac{x+40}{3}\)

Vì Chi có số nhãn vở ít hơn trung bình cộng của ba bạn 6 cái nên:

\(x-\dfrac{x+40}{3}=6\)

\(3x-\left(x+40\right)=18\)

\(2x-40=18\)

\(2x=58\)

\(x=29\) (nhãn) (thỏa mãn điều kiện)

Vậy Chi có \(29\) nhãn vở.

a: \(-\dfrac{4}{15}=\dfrac{3}{5}-\dfrac{13}{15}=\dfrac{3}{5}+\left(-\dfrac{13}{15}\right)\)

b: \(-\dfrac{4}{15}=\dfrac{-2}{5}\cdot\dfrac{2}{3}\)

c: \(-\dfrac{4}{15}=\dfrac{-2}{5}\cdot\dfrac{2}{3}=\dfrac{-2}{5}:\dfrac{3}{2}\)

Tỉ số giữa số sản phẩm xưởng thứ nhất làm được so với số sản phẩm xưởng thứ hai làm được là:

\(\dfrac{1}{3}:\dfrac{1}{5}=\dfrac{5}{3}\)

Số sản phẩm xưởng thứ nhất làm được là:

324:(5-3)x5=324:2x5=810(sản phẩm)

Số sản phẩm xưởng thứ hai làm được là:

810-324=486(sản phẩm)

Tỉ số giữa số sản phẩm xưởng thứ nhất làm được so với số sản phẩm xưởng thứ hai làm được:

     \(\dfrac{1}{3}:\dfrac{1}{5}=\dfrac{5}{3}\)

Ta có sơ đồ sau:

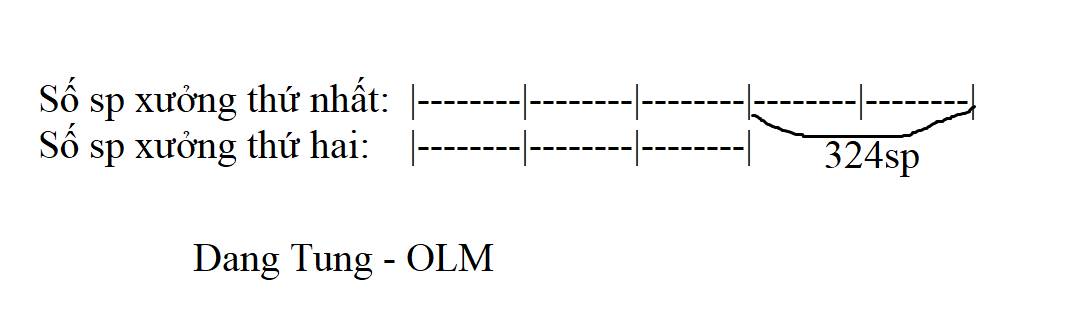 Hiệu số phần bằng nhau:

   5 - 3 = 2 (phần)

Số sản phẩm xưởng thứ nhất làm được:

  324 : 2 x 5 = 810 (sản phẩm)

Số sản phẩm xưởng thứ hai làm được:

  810 - 324 = 486 (sản phẩm)

Số tuổi của bố sau 5 năm là:

    27: (4 - 1) x 4 = 36 ( tuổi )

Số tuổi của bố hiện nay là:

   36 - 5 = 31 ( tuổi )

Số tuổi của con hiện nay là:

   31 - 27 = 4 (tuổi)

       Đ/s:......

Đặt tuổi của con hiện tại là xx tuổi.

Theo đề bài:

1. Bố lớn hơn con 27 tuổi, do đó tuổi của bố hiện tại là $x+27$.
2. Sau 5 năm nữa, tuổi bố sẽ gấp 4 lần tuổi con.

Sau 5 năm nữa:

• Tuổi con sẽ là $x+5$.
• Tuổi bố sẽ là $(x+27)+5=x+32$.

Theo điều kiện thứ 2 trong đề bài: $x+32=4\cdot (x+5)$

Giải phương trình này: $x+32=4x+20$ $32-20=4x-x$ $12=3x$ x=123=4x = \frac{12}{3} = 4x = 312 ​= 4

Vậy, tuổi của con hiện nay là $x=4$ tuổi.

Tuổi của bố: $x+27=4+27=31$ tuổi.

Vậy, tuổi của con hiện nay là 4 tuổi và tuổi của bố hiện nay là 31 tuổi.

Bạn Vương bạn Mừng ở đâu ra vậy em?