Phỏng vấn 100 khách hàng về nhu cầu sử dụng dịch vụ của một công ty: trong 100 khách hàng phỏng vấn, có 17 khách hàng trả lời “sẽ sử dụng", 48 khách hàng trả lời "có thể sẽ sử dụng” và 35 khách hàng trả lời “không sử dụng". Chọn ngẫu nhiên một khách hàng tính xác suất để khách hàng đó sử dụng dịch vụ của công ty, biết rằng tỷ lệ khách hàng sự sẽ sử dụng dịch vụ tương ứng với cách trả lời trên là: 0,4,0,2 và 0.01.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(A_1\) là biến cố: "2 sản phẩm lấy nhầm từ lô 1 đều là sản phẩm tốt"
\(A_2\) là biến cố: "2 sản phẩm lấy nhầm từ lô 1 có 1 sản phẩm tốt 1 sản phẩm xấu"
`A_3` là biến cố: "2 sản phẩm lấy nhầm từ lô 1 đều là sản phẩm xấu"
\(\Rightarrow P\left(A_1\right)=\dfrac{C_6^2}{C_9^2}=\dfrac{5}{12}\); \(P\left(A_2\right)=\dfrac{C_6^1.C_3^1}{C_9^2}=\dfrac{1}{2}\); \(P\left(A_3\right)=\dfrac{C_3^2}{C_9^2}=\dfrac{1}{12}\)
\(A_1;A_2;A_3\) tạo thành 1 nhóm biến cố đầy đủ
Gọi B là biến cố: "sản phẩm cuối cùng lấy ra là sản phẩm tốt"
\(\Rightarrow P\left(B|A_1\right)=\dfrac{5+2}{7+2}=\dfrac{7}{9}\);
\(P\left(B|A_2\right)=\dfrac{5+1}{7+2}=\dfrac{2}{3}\);
\(P\left(B|A_3\right)=\dfrac{5}{7+2}=\dfrac{5}{9}\)
a.
\(P\left(B\right)=P\left(A_1\right).P\left(B|A_1\right)+P\left(A_2\right).P\left(B|A_2\right)+P\left(A_3\right).P\left(B|A_3\right)\)
\(=\dfrac{5}{12}.\dfrac{7}{9}+\dfrac{1}{2}.\dfrac{2}{3}+\dfrac{1}{12}.\dfrac{5}{9}=\dfrac{19}{27}\)
b.
Gọi `C_1` là biến cố "sản phẩm cuối cùng lấy ra thuộc lô 1"
`C_2` là biến cố: "sản phẩm cuối cùng lấy ra thuộc lô 2"
\(\Rightarrow P\left(C_1\right)=\dfrac{2}{9};P\left(C_2\right)=\dfrac{7}{9}\)
`C_1`, `C_2` cũng là nhóm biến cố đầy đủ
\(P\left(B|C_1\right)=\dfrac{6}{9}=\dfrac{2}{3}\)
\(\Rightarrow P\left(C_1|B\right)=\dfrac{P\left(B|C_1\right).P\left(C_1\right)}{P\left(B\right)}=\dfrac{\dfrac{2}{3}.\dfrac{2}{9}}{\dfrac{19}{27}}=\dfrac{4}{19}\)
c.
\(P\left(A_2|B\right)=\dfrac{P\left(B|A_2\right).P\left(A_2\right)}{P\left(B\right)}=\dfrac{\dfrac{2}{3}.\dfrac{1}{2}}{\dfrac{19}{27}}=\dfrac{9}{19}\)

a) \(\dfrac{x+2004}{x+2005}+\dfrac{x+2005}{2006}< \dfrac{x+2006}{2007}+\dfrac{x+2007}{2008}\\ \Rightarrow\left(\dfrac{x+2004}{2005}-1\right)+\left(\dfrac{x+2005}{2006}-1\right)< \left(\dfrac{x+2006}{2007}-1\right)+\left(\dfrac{x+2007}{2008}-1\right)\\ \Rightarrow\dfrac{x-1}{2005}+\dfrac{x-1}{2006}< \dfrac{x-1}{2007}+\dfrac{x-1}{2008}\\ \Rightarrow\dfrac{x-1}{2005}+\dfrac{x-1}{2006}-\dfrac{x-1}{2007}-\dfrac{x-1}{2008}< 0\\ \)
\(\Rightarrow\left(x-1\right)\left(\dfrac{1}{2005}+\dfrac{1}{2006}-\dfrac{1}{2007}-\dfrac{1}{2008}\right)< 0\left(a\right)\)
Nhận thấy: \(\dfrac{1}{2005}>\dfrac{1}{2007},\dfrac{1}{2006}>\dfrac{1}{2008}\\ \Rightarrow\dfrac{1}{2005}-\dfrac{1}{2007}>0,\dfrac{1}{2006}-\dfrac{1}{2008}>0\\ \Rightarrow\dfrac{1}{2005}+\dfrac{1}{2006}-\dfrac{1}{2007}-\dfrac{1}{2008}>0\)
\(\left(a\right)\Rightarrow x-1< 0\Leftrightarrow x< 1\)
Vậy \(S=\left\{x|x< 1\right\}\)
b) \(\dfrac{x-2}{2002}+\dfrac{x-4}{2000}< \dfrac{x-3}{2001}+\dfrac{x-5}{1999}\\ \Rightarrow\left(\dfrac{x-2}{2002}-1\right)+\left(\dfrac{x-4}{2000}-1\right)< \left(\dfrac{x-3}{2001}-1\right)+\left(\dfrac{x-5}{1999}-1\right)\\ \Rightarrow\dfrac{x-2004}{2002}+\dfrac{x-2004}{2000}< \dfrac{x-2004}{2001}+\dfrac{x-2004}{1999}\\ \Rightarrow\dfrac{x-2004}{2002}+\dfrac{x-2004}{2000}-\dfrac{x-2004}{2001}-\dfrac{x-2004}{1999}< 0\\ \)
\(\Rightarrow\left(x-2004\right)\left(\dfrac{1}{2002}+\dfrac{1}{2000}-\dfrac{1}{2001}-\dfrac{1}{1999}\right)< 0\left(b\right)\)
Nhận thấy: \(\dfrac{1}{2002}< \dfrac{1}{2001},\dfrac{1}{2000}< \dfrac{1}{1999}\Rightarrow\dfrac{1}{2002}-\dfrac{1}{2001}< 0,\dfrac{1}{2000}-\dfrac{1}{1999}< 0\\ \Rightarrow\dfrac{1}{2002}+\dfrac{1}{2000}-\dfrac{1}{2001}-\dfrac{1}{1999}< 0\)
\(\left(b\right)\Rightarrow x-2004>0\Leftrightarrow x>2004\)

\(a,\dfrac{x+2}{6}+\dfrac{x+5}{3}>\dfrac{x+3}{5}+\dfrac{x+6}{2}\\ < =>\left(\dfrac{x+2}{6}+1\right)+\left(\dfrac{x+5}{3}+1\right)>\left(\dfrac{x+3}{5}+1\right)+\left(\dfrac{x+6}{2}+1\right)\\ < =>\dfrac{x+8}{6}+\dfrac{x+8}{3}>\dfrac{x+8}{5}+\dfrac{x+8}{2}\\ < =>\dfrac{x+8}{5}+\dfrac{x+8}{2}-\dfrac{x+8}{6}-\dfrac{x+8}{2}< 0\\ < =>\left(x+8\right)\left(\dfrac{1}{5}+\dfrac{1}{2}-\dfrac{1}{6}-\dfrac{1}{3}\right)< 0\)
Mà: `1/5+1/2+1/6-1/3>0`
`=>x+8<0`
`<=>x<-8`
\(\dfrac{x-2}{1007}+\dfrac{x-1}{1008}< \dfrac{2x-1}{2017}+\dfrac{2x-3}{2015}\\ < =>\left(\dfrac{x-2}{1007}-1\right)+\left(\dfrac{x-1}{1008}-1\right)< \left(\dfrac{2x-1}{2017}-1\right)+\left(\dfrac{2x-3}{2015}-1\right)\\ < =>\dfrac{x-1009}{1007}+\dfrac{x-1009}{1008}< \dfrac{2x-2018}{2017}+\dfrac{2x-2018}{2015}\\ < =>\dfrac{x-1009}{1007}+\dfrac{x-1009}{1008}-\dfrac{2\left(x-1009\right)}{2017}-\dfrac{2\left(x-1009\right)}{2015}< 0\\ < =>\left(x-1009\right)\left(\dfrac{1}{1007}+\dfrac{1}{1008}-\dfrac{2}{2017}-\dfrac{2}{2015}\right)< 0\)
Mà: `1/1006+1/1008-2/2017-2/2015>0`
`=>x-1009<0`
`<=>x<1009`

a/
Gọi x là số phút gọi thỏa mãn đề bài
\(32+\left(x-45\right).0,4=44+0,25x\)
\(\Leftrightarrow32+0,4x-18=44+0,25x\)
\(\Leftrightarrow0,15x=30\Rightarrow x=200\)
b/
+Nếu KH gọi 180 phút trong 1 tháng thì
Số tiền cho gói cước A là \(32+\left(180-45\right).0,4=86\) USD
Số tiền cho gói cước B là \(44+180.0,25=89\) USD
Trong trường hợp này chọn gói cước A có lợi hơn
+ Trường hợp KH gọi 500 phút thì
Số tiền cho gói cước A: \(32+\left(500-45\right).0,4=214\) USD
Số tiền cho gói cước B: \(44+500.0,25=169\) USD
Trong trường hợp này chọn gói cước B có lợi hơn

a) `(x+4)(y-1)=13`
Ta có bảng:
| x + 4 | 1 | -1 | 13 | -13 |
| y - 1 | 13 | -13 | 1 | -1 |
| x | -3 | -5 | 9 | -17 |
| y | 14 | -12 | 2 | 0 |
b) `xy-3x+y=20`
`=>(xy-3x)+(y-3)=20-3`
`=>x(y-3)+(y-3)=17`
`=>(y-3)(x+1)=17`
Ta có bảng:
| y - 3 | 17 | -1 | -17 | 1 |
| x + 1 | 1 | -17 | -1 | 17 |
| y | 20 | 2 | -14 | 4 |
| x | 0 | -18 | -2 | 16 |

a) 10 ⋮ (x - 1)
⇒ x - 1 ∈ Ư(10) = {-10; -5; -2; -1; 1; 2; 5; 10}
⇒ x ∈ {-9; -4; -1; 0; 2; 3; 6; 11}
b) x + 5 = x - 2 + 7
Để (x - 5) ⋮ (x - 2) thì 7 ⋮ (x - 2)
⇒ x - 2 ∈ Ư(7) = {-7; -1; 1; 7}
⇒ x ∈ {-5; 1; 3; 9}
c) 3x + 8 = 3x - 3 + 11
= 3(x - 1) + 11
Để (3x + 8) ⋮ (x - 3) thì 11 ⋮ (x - 3)
⇒ x - 3 ∈ Ư(11) = {-11; -1; 1; 11}
⇒ x ∈ {-8; 2; 4; 14}

a) 25 chia hết cho n + 2
=> n + 2 ∈ Ư(25)
=> n + 2 ∈ {1; -1; 5; -5; 25; -25}
=> n ∈ {-1; -3; 3; -7; 23; -27}
b) 2n + 4 chia hết cho n - 1
=> (2n - 2) + 6 chia hết chi n - 1
=> 2(n - 1) + 6 chia hết cho n - 1
=> 6 chia hết cho n - 1
=> n - 1 ∈ Ư(6) = {1; -1; 2; -2; 3; -3; 6; -6}
=> n ∈ {2; 0; 3; -1; 4; -2; 7; -5}
a) 25 ⋮ (n + 2)
⇒ n + 2 ∈ Ư(25) = {-25; -5; -1; 1; 5; 25}
⇒ n ∈ {-27; -7; -3; -1; 3; 23}
b) 2n + 4 = 2n - 2 + 6
= 2(n - 1) + 6
Để (2n + 4) ⋮ (n - 1) thì 6 ⋮ (n - 1)
⇒ n - 1 ∈ Ư(6) = {-6; -3; -2; -1; 1; 2; 3; 6}
⇒ n ∈ {-5; -2; -1; 0; 2; 3; 4; 7}

Bài 11.2
\(a,A=3+3^2+3^3+....+3^{99}\\ =\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+....+\left(3^{97}+3^{98}+3^{99}\right)\\ =3\cdot\left(1+3+9\right)+3^4\cdot\left(1+3+9\right)+...+3^{97}\cdot\left(1+3+9\right)\\ =13\cdot\left(3+3^4+....+3^{97}\right)⋮13\\ b,B=5+5^2+...+5^{50}\\ =\left(5+5^2\right)+\left(5^3+5^4\right)+..+\left(5^{49}+5^{50}\right)\\ =5\cdot\left(1+5\right)+5^3\cdot\left(1+5\right)+....+5^{49}\cdot\left(1+5\right)\\ =6\cdot\left(5+5^3+...+5^{49}\right)⋮6\)
Bài 11.4:
a: \(10⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
=>\(x\in\left\{2;0;3;-1;6;-4;11;-9\right\}\)
b:
\(x+5⋮x-2\)
=>\(x-2+7⋮x-2\)
=>\(7⋮x-2\)
=>\(x-2\in\left\{1;-1;7;-7\right\}\)
=>\(x\in\left\{3;1;9;-5\right\}\)
c: \(3x+8⋮x-1\)
=>\(3x-3+11⋮x-1\)
=>\(11⋮x-1\)
=>\(x-1\in\left\{1;-1;11;-11\right\}\)
=>\(x\in\left\{2;0;12;-10\right\}\)
Bài 11.5:
a: (x+4)(y-1)=13
=>\(\left(x+4;y-1\right)\in\left\{\left(1;13\right);\left(13;1\right);\left(-1;-13\right);\left(-13;-1\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(-3;14\right);\left(9;2\right);\left(-5;-12\right);\left(-17;0\right)\right\}\)
b: xy-3x+y=20
=>x(y-3)+y-3=17
=>(x+1)(y-3)=17
=>\(\left(x+1;y-3\right)\in\left\{\left(1;17\right);\left(17;1\right);\left(-1;-17\right);\left(-17;-1\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(0;20\right);\left(16;4\right);\left(-2;-14\right);\left(-18;2\right)\right\}\)

a) Ta có:
`m^2>=0` với mọi m
`=>m^2+1/2>=1/2>0` với mọi m
`=>` Bất pt: `(m^2+1/2)x-1<=0` có hệ số `a≠0`
`=>`Bất pt luôn là bất pt bậc nhất 1 ẩn với mọi m
b) Ta có:
`m^2+m+2=(m^2+2*m*1/2+1/4)+7/4`
`=(m+1/2)^2+7/4>=7/4>=0` với mọi m
`=>-(m^2+m+2)<=-7/2<0` với mọi m
`=>-(m^2+m+2)≠0` với mọi m
=> Bất pt `-(m^2+m+2)x<=-m+2024` luôn là bpt bậc nhất 1 ẩn
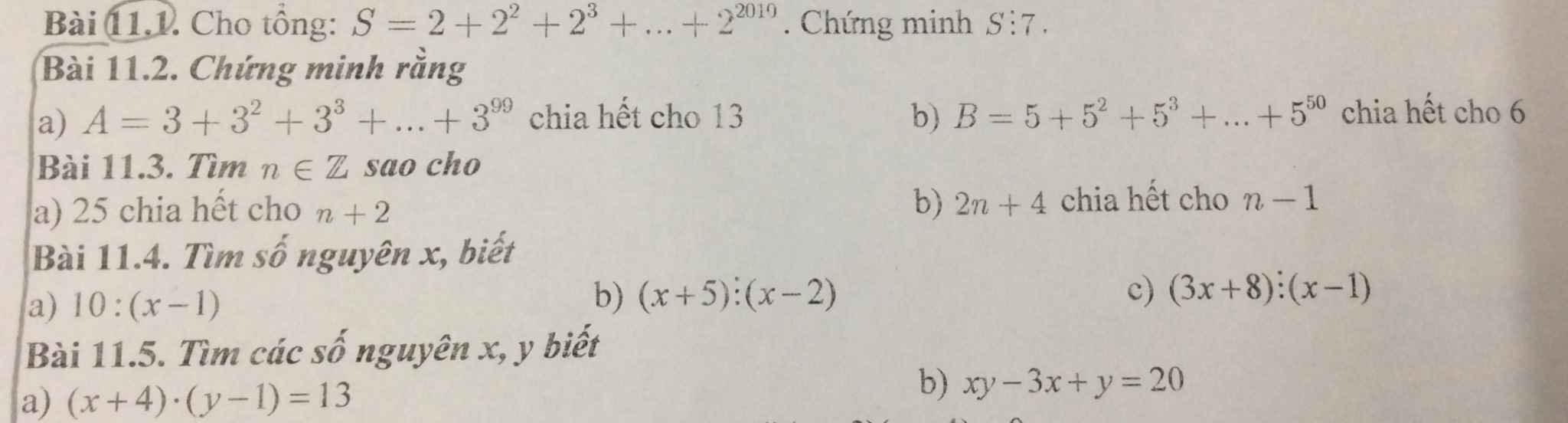
Gọi A, B, C lần lượt là các biến cố: "Khách hàng trả lời "sẽ sử dụng"."; "Khách hàng trả lời "có thể sẽ sử dụng"." và "Khách hàng trả lời "không sử dụng"." và X là biến cố: "Khách hàng sử dụng dịch vụ."
Khi đó theo đề bài, ta có \(P\left(A\right)=\dfrac{17}{100};P\left(B\right)=\dfrac{48}{100};P\left(C\right)=\dfrac{35}{100};P\left(X|A\right)=0,4;P\left(X|B\right)=0,2;P\left(X|C\right)=0,01\)
Theo công thức xác suất đầy đủ:
\(P\left(X\right)=P\left(A\right)P\left(X|A\right)+P\left(B\right)P\left(X|B\right)+P\left(C\right)P\left(X|C\right)\)
\(=\dfrac{17}{100}.0,4+\dfrac{48}{100}.0,2+\dfrac{35}{100}.0,01=\dfrac{67}{400}=0,1675=16,75\%\)
Vậy tỉ lệ khách hàng sử dụng dịch vụ là \(16,75\%\)
Gọi \(A_1\) là biến cố: "khách hàng được chọn thuộc nhóm trả lời sẽ sử dụng"
`A_2` là biến cố: "khách hàng được chọn thuộc nhóm trả lời có thể sẽ sử dụng"
`A_3` là biến cố: "khách hàng được chọn thuộc nhóm trả lời không sử dụng"
\(\Rightarrow P\left(A_1\right)=\dfrac{17}{100}\) ; \(P\left(A_2\right)=\dfrac{48}{100}\); \(P\left(A_3\right)=\dfrac{35}{100}\)
\(A_1;A_2;A_3\) tạo thành 1 nhóm biến cố đầy đủ
Gọi B là biến cố: "khách hàng đó sử dụng dịch vụ của công ty"
\(\Rightarrow P\left(B|A_1\right)=0,4\); \(P\left(B|A_2\right)=0,2\); \(P\left(B|A_3\right)=0,01\)
Theo công thức xác suất đầy đủ:
\(P\left(B\right)=0,4\times\dfrac{17}{100}+0,2\times\dfrac{48}{100}+0,01\times\dfrac{35}{100}=0,1675\)