Một lớp học có 50 học sinh gồm ba loại học lực giỏi, khá, trung bình. Biết số học sinh học lực trung bình bằng 2/3 số học sinh học lực khác và số học sinh học lực khá bằng 12/5 số học sinh học lực giỏi, tính số học sinh mỗi loại của lớp đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu a
A = m\(x^2\) + 2 - 1
\(x=1\) là nghiệm của A khi và chỉ khi:
m.1\(^2\) + 2 - 1 = 0
m + 2 - 1 = 0
m = 1 - 2
m = -1
Vậy m = - 1 thì \(x=1\) là nghiệm của A
b; B = \(x^2\) + m\(x\) - 3
\(x=1\) là nghiệm của B khi và chỉ khi
1\(^2\) + m.1 - 3 = 0
1 + m - 3 = 0
m = 3 - 1
m = 2
Vậy với m = 2 thì \(x=1\) là nghiệm của B


Xét ΔABK có \(\widehat{BKC}\) là góc ngoài tại đỉnh K
nên \(\widehat{BKC}=\widehat{KAB}+\widehat{KBA}=90^0+\widehat{KBA}>90^0\)
Xét ΔBKC có \(\widehat{BKC}>90^0\)
nên BC là cạnh lớn nhất trong ΔBKC
=>BC>BK

a-2ab+2b=0
=>\(a-2b\left(a-1\right)=0\)
=>\(a-1-2b\left(a-1\right)=-1\)
=>\(\left(a-1\right)\left(1-2b\right)=-1\)
=>(a-1)(2b-1)=1
=>\(\left(a-1;2b-1\right)\in\left\{\left(1;1\right);\left(-1;-1\right)\right\}\)
=>\(\left(a;b\right)\in\left\{\left(2;1\right);\left(0;0\right)\right\}\)

a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-60^0=30^0\)
b: Xét ΔBAH và ΔBKH có
BA=BK
HA=HK
BH chung
Do đó: ΔBAH=ΔBKH
c: ΔBAH=ΔBKH
=>\(\widehat{BHA}=\widehat{BHK}\)
mà \(\widehat{BHA}+\widehat{BHK}=180^0\)(hai góc kề bù)
nên \(\widehat{BHA}=\widehat{BHK}=\dfrac{180^0}{2}=90^0\)
=>BI\(\perp\)AK tại H

Vì DE = DF (giả thiết)
DM = DN (giả thiết)
=> DE - DM = DF - DN
=> ME = NF
Xét tam giác DME và tam giác DNF có:
DE = DF (giả thiết)
góc D chung
DM = DN (giả thiết)
=> tam giác DME = tam giác DNF (cạnh - góc - cạnh) => ME = NF (2 cạnh tương ứng) b, Xét tam giác MEF và tam giác NFE có: ME = NF (chứng minh trên)
EF chung
MF = NE (chứng minh trên)
=> tam giác MEF = tam giác NFE (cạnh - cạnh - cạnh) c, I: Xét tam giác DME và tam giác DNF có: DE = DF (giả thiết)
góc D chung
DM = DN (giả thiết)
=> tam giác DME = tam giác DNF (cạnh - góc - cạnh) => góc DEM = góc DFN (2 góc tương ứng) Mà góc DEM + góc MEN = 180 độ (2 góc kề bù)
góc DFN + góc MFE = 180 độ (2 góc kề bù)
=> góc MEN = góc MFE
Xét tam giác EMI và tam giác FNI có:
ME = NF (chứng minh trên)
góc EMI = góc FNI (2 góc đối đỉnh)
góc MEN = góc MFE (chứng minh trên)
=> tam giác EMI = tam giác FNI (góc - cạnh - góc)

a) Xét \(\Delta DNE\) và \(\Delta DMF\) có:
\(DN=DM\left(gt\right)\)
\(\widehat{D}\) chung
\(DE=DF\left(gt\right)\)
\(\Rightarrow\Delta DNE=\Delta DMF\left(c-g-c\right)\)
\(\Rightarrow NE=MF\) (hai cạnh tương ứng)
b) Ta có:
\(ME=DE-DM\)
\(NF=DF-DN\)
Mà \(DE=DF\left(gt\right)\)
\(DM=DN\left(gt\right)\)
\(\Rightarrow ME=NF\)
Xét \(\Delta MEF\) và \(\Delta NFE\) có:
\(ME=NF\left(cmt\right)\)
\(MF=NE\left(cmt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta MEF=\Delta NFE\left(c-c-c\right)\)
c) Do \(\Delta DNE=\Delta DMF\left(cmt\right)\)
\(\Rightarrow\widehat{DEN}=\widehat{DFM}\) (hai góc tương ứng)
\(\Rightarrow\widehat{MEI}=\widehat{NFI}\)
Do \(\Delta MEF=\Delta NFE\left(cmt\right)\)
\(\Rightarrow\widehat{EMF}=\widehat{FNE}\) (hai góc tương ứng)
\(\Rightarrow\widehat{EMI}=\widehat{FNI}\)
Xét \(\Delta EMI\) và \(\Delta FNI\) có:
\(\widehat{MEI}=\widehat{NFI}\left(cmt\right)\)
\(ME=NF\left(cmt\right)\)
\(\widehat{EMI}=\widehat{FNI}\left(cmt\right)\)
\(\Rightarrow EMI\Delta=\Delta FNI\left(g-c-g\right)\)

Gọi: Chiều dài là x, chiều rộng là y
Theo đề bài ra, ta có: \(\frac{S_1}{S_2}=\frac45;\frac{S_2}{S_3}=\frac78;x_1=x_2;y_1+y_2=27;y_2=y_3;x_3=24\)
Mà \(x_1=x_2;\frac{S_1}{S_2}=\frac45\Rightarrow\frac{y_1}{y_2}=\frac45\)
Vậy: Chiều rộng của hình chữ nhật thứ nhất là: \(\frac{27}{\left(4+5\right)}\times4=12\left(\operatorname{cm}\right)\)
Chiều rộng của hình chữ nhật thứ hai hoặc ba là: \(27-12=15\left(\operatorname{cm}\right)\)
Diện tích của hình chữ nhật thứ 3 là: \(15\times24=360\left(\operatorname{cm}\right)\)
Diện tích của hình chữ nhật thứ 2 là: \(360\times\frac78=315\left(\operatorname{cm}\right)\)
Diện tích của hình chữ nhật thứ 1 là: \(315\times\frac45=252\left(\operatorname{cm}\right)\)

\(\left\{{}\begin{matrix}x_1=3y_1\\2y_1-x_1=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=3y_1\\2y_1-3y_1=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-y_1=-7\\x_1=3y_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_1=7\\x_1=3\cdot7=21\end{matrix}\right.\)
x và y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{21}{45}=\dfrac{7}{y_2}\)
=>\(\dfrac{7}{y_2}=\dfrac{7}{15}\)
=>\(y_2=15\)
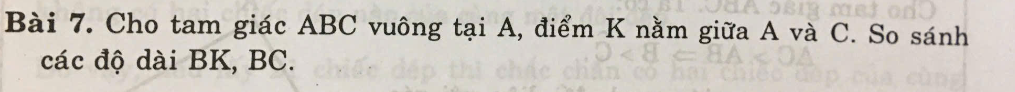
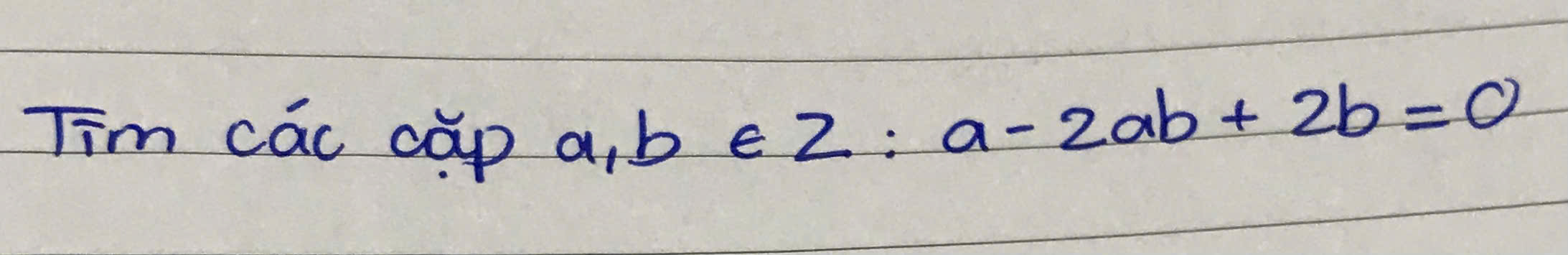

Giải:
Gọi số học sinh giỏi là \(x\) (học sinh); (\(x\) ∈ N*)
Khi đó, số học sinh khá là: \(\frac{12}{5}\)\(x\) (học sinh)
Số học sinh trung bình là: \(\frac{12}{5}x\times\) \(\frac23\) = \(\frac{24}{15}x\)(học sinh)
Theo bài ra ta có phương trình:
\(\frac{24}{15}x\) + \(\frac{12}{5}x\) + \(x\) = 50
\(x\) .(\(\frac{24}{15}\) + \(\frac{12}{5}\) + 1) = 50
\(x\) .(\(\frac{24}{15}\) + \(\frac{36}{15}\) + \(\frac{15}{15}\)) = 50
\(x\) .\(\left(\frac{60}{15}+\frac{15}{15}\right)\) = 50
\(\frac{x.75}{15}\) = 50
\(x\) = 50 x 15 : 75
\(x=10\)
Vậy số học sinh giỏi là 10 học sinh
Số học sinh khá là 10 x \(\frac{12}{5}\) = 24 (học sinh)
Số học sinh trung bình là: 50 - 24 - 10 = 16 (học sinh)
Kết luận: Học sinh trung bình là 16 học sinh
Học sinh khá là 24 học sinh
Học sinh giỏi là 10 học sinh.
sai lớp học nhé bạn