Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2}}}}\)
\(=2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{\dfrac{5}{2}}}}\)
\(=2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{2}{5}}}\)
\(=2+\dfrac{1}{2+\dfrac{1}{\dfrac{12}{5}}}\)
\(=2+\dfrac{1}{2+\dfrac{5}{12}}\)
\(=2+\dfrac{1}{\dfrac{29}{12}}\)
\(=2+\dfrac{12}{29}=\dfrac{70}{29}\)

Thể tích của hộp chữ nhật được tính theo công thức: V = chiều dài x chiều rộng x chiều cao.
Theo đề bài, chiều cao là 1 (cm), chiều rộng là x (cm) và chiều dài hơn chiều rộng là 3 (cm).
Do đó, chiều dài là x + 3 (cm).
Thay giá trị vào công thức, ta có:
V = (x + 3) x x x 1
= x(x + 3)
Do đó, thể tích của hộp chữ nhật được tính theo x là V = x(x + 3).
...

Bài 1:
$|x|=\frac{1}{3}\Rightarrow x=\frac{1}{3}$ hoặc $x=\frac{-1}{3}$
Nếu $x=\frac{1}{3}$ thì $A=3x^2-4x+5=3.(\frac{1}{3})^2-4.\frac{1}{3}+5=4$
Nếu $x=\frac{-1}{3}$ thì $A=3x^2-4x+5=3.(\frac{-1}{3})^2-4.\frac{-1}{3}+5=\frac{20}{3}$
Baif 2:
$|x|=2\Rightarrow x=\pm 2$
Nếu $x=2$ thì $B=-2x^2+3x-2=-2.2^2+3.2-2=-4$
Nếu $x=-2$ thì $B=-2x^2+3x-2=-2.(-2)^2+3(-2)-2=-16$
Bài 3:
Nếu $x\geq 5$ thì:
$C=2(5x+2)-(x-5)=10x+4-x+5=9x+9$
Nếu $x<5$ thì:
$C=2(5x+2)-(5-x)=10x+4-5+x=11x-1$

Để đơn giản hóa biểu thức, chúng ta cần áp dụng thuộc tính phân phối và đơn giản hóa mọi giá trị tuyệt đối.
Đầu tiên, hãy phân phối 3 cho các điều khoản bên trong dấu ngoặc đơn:
3(4x-1) = 12x - 3
Tiếp theo, hãy đơn giản hóa biểu thức giá trị tuyệt đối |x-2|:
|x-2| có thể dương hoặc âm tùy thuộc vào giá trị của x. Nếu x lớn hơn 2 thì |x-2| = x-2. Nếu x nhỏ hơn 2 thì |x-2| = -(x-2) = -x + 2.
Do đó, chúng ta có hai trường hợp cần xem xét:
Trường hợp 1: x > 2
Trong trường hợp này, |x-2| = x-2. Vì vậy, biểu thức trở thành:
12x - 3 - (x-2)
Đơn giản hóa hơn nữa:
12x - 3 - x + 2 = 11x - 1
Trường hợp 2: x < 2
Trong trường hợp này, |x-2| = -x + 2. Vậy biểu thức trở thành:
12x - 3 - (-x + 2)
Đơn giản hóa hơn nữa:
12x - 3 + x - 2 = 13x - 5
Do đó, biểu thức đơn giản hóa là:
Nếu x > 2: 11x - 1
Nếu x < 2: 13x - 5
...


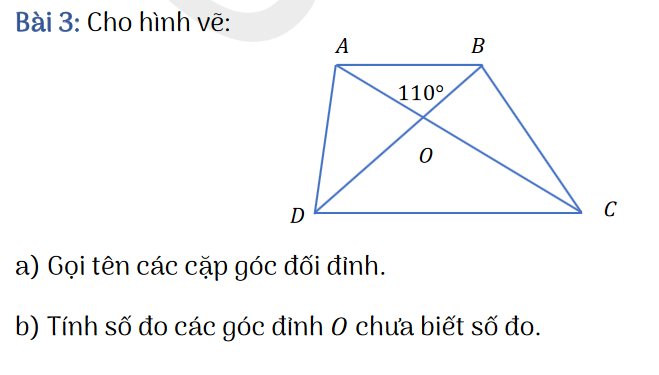
a, Các cặp góc đối đỉnh là: \(\widehat{AOB}\) và \(\widehat{COD}\), \(\widehat{AOD}\) và \(\widehat{BOC}\)
b, \(\widehat{COD}=\widehat{AOB}=110^o\)
\(\widehat{AOD}=\widehat{BOC}=180^o-110^o=70^o\)

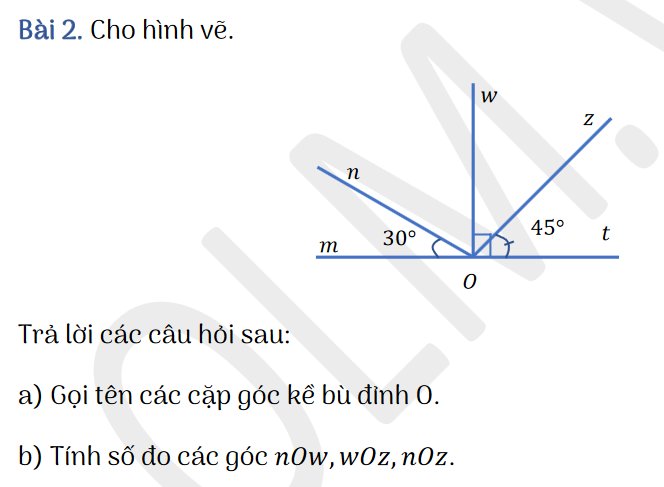
a) Góc nOm và góc nOt
góc mOw và góc tOw
góc zOt và góc mOz
b) Ta có : nOm+nOw=mOw
Mà nOm = 30 độ
mOw=90 độ
suy ra : nOw=90-30=60 độ
Ta có : wOz+zOt=wOt
suy ra: wOz = wOt-wOt=90-45=45 độ
Ta có : nOz=nOw+wOz=60+45=105 độ
a) \(\widehat{mOn;}\widehat{nOw};\widehat{wOZ};\widehat{zOt}\)
b) \(\widehat{nOw}=60^o;\widehat{wOz}=45^o;\widehat{nOz}=60^o+45^o=105^o\)

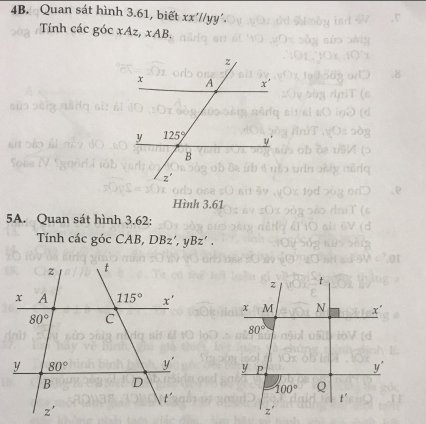
Bài 4B:
\(\widehat{xAB}\) = 1800 - 1250 = 550
\(\widehat{xAz}\) = \(\widehat{ABY}\) = 1250 (vì hai góc đồng vị)
5A.
\(\widehat{CAB}\) = 1800 - 800 = 1000
\(\widehat{CAB}\) = \(\widehat{DBZ'}\) = 1000 (hai góc đồng vị)
\(\widehat{YBZ'}\) = \(\widehat{ABD}\) = 800

\(x^3:\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)
\(\Rightarrow x^3:\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)
\(\Rightarrow x^3=\left(\dfrac{1}{2}\right)^2\cdot\dfrac{1}{2}\)
\(\Rightarrow x^3=\left(\dfrac{1}{2}\right)^3\)
\(\Rightarrow x=\dfrac{1}{2}\)
\(x^3:\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\Rightarrow x^3=\dfrac{1}{2}.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}.\left(\dfrac{1}{2}\right)^2=\left(\dfrac{1}{2}\right)^3\)
\(\Rightarrow x=\dfrac{1}{2}\)

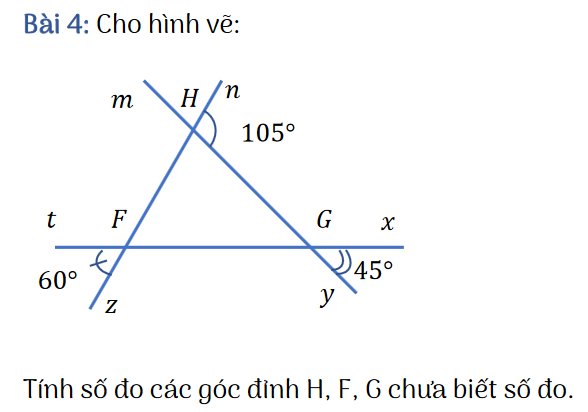
\(\widehat{mHF}=105^o\), \(\widehat{mHn}=\widehat{FHG}=180^o-105^o=75^o\)
\(\widehat{HFG}=60^o\), \(\widehat{HFt}=\widehat{GFz}=180^o-60^o=120^o\)
\(\widehat{HGF}=45^o\), \(\widehat{HGx}=\widehat{FGy}=180^o-45^o=135^o\)