
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
(x² - x + 1)(x² + x + 1)
= (x² + 1)² - x²
= x⁴ + 2x² + 1 - x²
= x⁴ + x² + 1
Vậy a = 1; b = 1

a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=30^0\)
XétΔABC có \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
mà AB,AC,BC lần lượt là cạnh đối diện của các góc ACB,ABC,BAC
nên AB<AC<BC
b: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
Do đó: ΔCAB=ΔCAD
=>CB=CD
c: AB=AD
=>A là trung điểm của BD
Xét ΔCDB có
CA,DK là các đường trung tuyến
CA cắt DK tại M
Do đó: M là trọng tâm của ΔCDB
=>\(AM=\dfrac{AC}{3}=\dfrac{8}{3}\left(cm\right)\)
d: Gọi I là trung điểm của AC
d là trung trực của AC
=>QI\(\perp\)AC tại I và I là trung điểm của AC
Ta có: QI\(\perp\)AC
AD\(\perp\)AC
Do đó: QI//AD
Xét ΔACD có
I là trung điểm của CA
IQ//AD
Do đó: Q là trung điểm của CD
Xét ΔCDB có
M là trọng tâm
Q là trung điểm của CD
Do đó: B,M,Q thẳng hàng

bài 1:
a: 2x=3y
=>\(\dfrac{x}{3}=\dfrac{y}{2}\)
mà x+y=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{20}{5}=4\)
=>\(x=4\cdot3=12;y=2\cdot4=8\)
b: Gọi số sách lớp 8A,8B quyên góp được lần lượt là a(quyển),b(quyển)
(Điều kiện: \(a,b\in Z^+\))
Số sách lớp 8A,8B quyên góp được lần lượt tỉ lệ với 3;4
=>\(\dfrac{a}{3}=\dfrac{b}{4}\)
Tổng số sách hai lớp quyên góp được là 70 quyển
=>a+b=70
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{a+b}{3+4}=\dfrac{70}{7}=10\)
=>\(a=10\cdot3=30;b=4\cdot10=40\)
Vậy: Lớp 8A quyên góp được 30 quyển; lớp 8B quyên góp được 40 quyển
Bài 2:
d: \(P\left(x\right)=4x^2+3x^3-6x+4x^3-5x^2\)
\(=\left(3x^3+4x^3\right)+\left(4x^2-5x^2\right)-6x\)
\(=7x^3-x^2-6x\)
e: \(P\left(x\right)=7x^3-x^2-6x\)
=>bậc là 3
f: \(P\left(1\right)=7\cdot1^3-1^2-6\cdot1=7-1-6=0\)
=>x=1 là nghiệm của P(x)
Bài 3:
a: A: "Quả bóng lấy ra có màu xanh"
=>n(A)=1
=>\(P_A=\dfrac{1}{6}\)
B: "Quả bóng lấy ra có màu đỏ"
=>n(B)=1
=>\(P_B=\dfrac{1}{6}\)
C: "Quả bóng lấy ra có màu trắng"
=>n(C)=4
\(P_C=\dfrac{4}{6}=\dfrac{2}{3}\)

Các cặp góc đối đỉnh là \(\widehat{xEA};\widehat{CED}\) và \(\widehat{AEC};\widehat{xED}\)
Các cặp góc kề bù là
\(\widehat{AEC};\widehat{DEC}\)
\(\widehat{AEC};\widehat{xEA}\)
\(\widehat{DEC};\widehat{xED}\)
\(\widehat{xED};\widehat{xEA}\)
Các cặp góc đồng vị là
\(\widehat{DEC};\widehat{DAB}\)
\(\widehat{DCE};\widehat{DBA}\)

\(B=4x-x^2+3\)
\(=-x^2+4x-4+7\)
\(=-\left(x-2\right)^2+7< =7\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2

\(E=\dfrac{3x^2-6x+17}{x^2-2x+3}=\dfrac{3x^2-6x+9+8}{x^2-2x+3}\)
\(=3+\dfrac{8}{x^2-2x+3}\)
\(=3+\dfrac{8}{x^2-2x+1+2}=3+\dfrac{8}{\left(x-1\right)^2+2}\)
\(\left(x-1\right)^2+2>=2\forall x\)
=>\(\dfrac{8}{\left(x-1\right)^2+2}< =\dfrac{8}{2}=4\forall x\)
=>\(E=3+\dfrac{8}{\left(x-1\right)^2+2}=4+3=7\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1

a) \(A\left(x\right)=2x^3-4x^2+3x-5\)
\(B\left(x\right)=3x^3+4x^2+2x+1\)
\(A\left(x\right)+B\left(x\right)=\left(2x^3-4x^2+3x-5\right)+\left(3x^3+4x^2+2x+1\right)\)
\(=2x^3-4x^2+3x-5+3x^3+4x^2+2x+1\)
\(=\left(2x^3+3x^3\right)+\left(-4x^2+4x^2\right)+\left(3x+2x\right)+\left(-5+1\right)\)
\(=5x^3+5x-4\)
b) \(x.\left(x^2-3\right)=x.x^2+x.\left(-3\right)=x^3-3x\)

a: Xét ΔBAH vuông tại H và ΔBEH vuông tại E có
BH chung
\(\widehat{ABH}=\widehat{EBH}\)
Do đó: ΔBAH=ΔBEH
b: Vì I là giao điểm của BH và DC
nên \(I\in BH\)
=>B,H,I thẳng hàng

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔDBE và ΔDHA có
DB=DH
\(\widehat{BDE}=\widehat{HDA}\)(hai góc đối đỉnh)
DE=DA
Do đó: ΔDBE=ΔDHA
=>BE=HA
Xét ΔBAE có BA+BE>AE
=>AC+AH>2AD
c: Ta có: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
\(CD=CH+HD=CH+\dfrac{1}{2}HB=\dfrac{3}{2}HC\)
=>\(CH=\dfrac{2}{3}CD\)
Xét ΔCAE có
CD là đường trung tuyến
\(CH=\dfrac{2}{3}CD\)
Do đó: H là trọng tâm của ΔCAE
Xét ΔCAE có
H là trọng tâm
K là trung điểm của CE
Do đó: A,H,K thẳng hàng



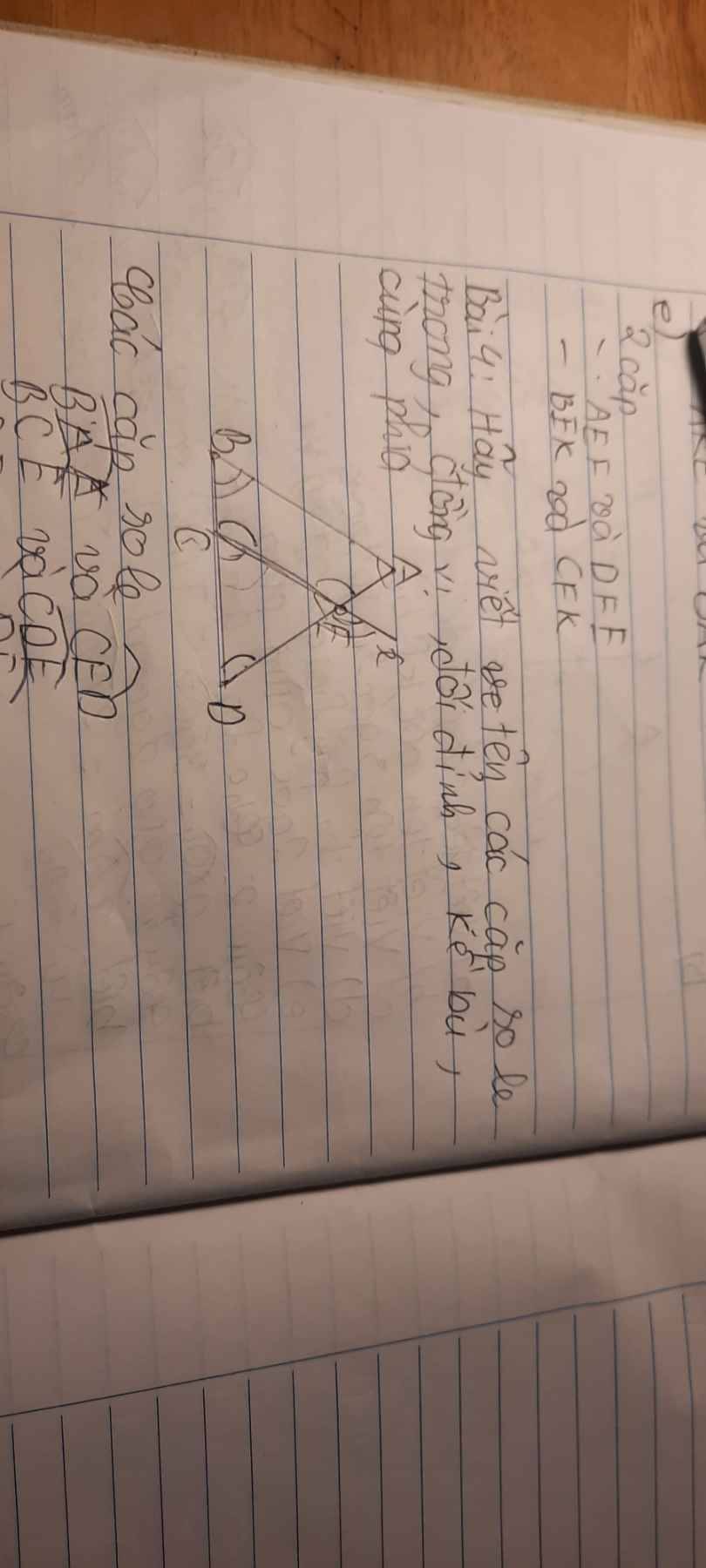



b của em đâu nhỉ?
\(2x^3-5x^2+x+a⋮x^2-3x+2\)
=>\(2x^3-6x^2+4x+x^2-3x+2+a-2⋮x^2-3x+2\)
=>a-2=0
=>a=2