
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A\left(x\right)=2x^3-4x^2+3x-5\)
\(B\left(x\right)=3x^3+4x^2+2x+1\)
\(A\left(x\right)+B\left(x\right)=\left(2x^3-4x^2+3x-5\right)+\left(3x^3+4x^2+2x+1\right)\)
\(=2x^3-4x^2+3x-5+3x^3+4x^2+2x+1\)
\(=\left(2x^3+3x^3\right)+\left(-4x^2+4x^2\right)+\left(3x+2x\right)+\left(-5+1\right)\)
\(=5x^3+5x-4\)
b) \(x.\left(x^2-3\right)=x.x^2+x.\left(-3\right)=x^3-3x\)

a: Xét ΔBAH vuông tại H và ΔBEH vuông tại E có
BH chung
\(\widehat{ABH}=\widehat{EBH}\)
Do đó: ΔBAH=ΔBEH
b: Vì I là giao điểm của BH và DC
nên \(I\in BH\)
=>B,H,I thẳng hàng

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔDBE và ΔDHA có
DB=DH
\(\widehat{BDE}=\widehat{HDA}\)(hai góc đối đỉnh)
DE=DA
Do đó: ΔDBE=ΔDHA
=>BE=HA
Xét ΔBAE có BA+BE>AE
=>AC+AH>2AD
c: Ta có: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
\(CD=CH+HD=CH+\dfrac{1}{2}HB=\dfrac{3}{2}HC\)
=>\(CH=\dfrac{2}{3}CD\)
Xét ΔCAE có
CD là đường trung tuyến
\(CH=\dfrac{2}{3}CD\)
Do đó: H là trọng tâm của ΔCAE
Xét ΔCAE có
H là trọng tâm
K là trung điểm của CE
Do đó: A,H,K thẳng hàng

Giải:
2cm + 4cm = 6cm (loại) vì tổng hai cạnh của một tam giác luôn lớn hơn độ dài cạnh còn lại
1cm + 3cm = 4cm < 5cm (loại vì tổng hai cạnh của một tam giác luôn lớn hơn độ dài cạnh còn lại)
2cm + 3cm = 5cm > 4cm (thỏa mãn)
2cm + 3cm = 5cm (loại vì tổng hai cạnh của một tam giác luôn lớn hơn độ dài cạnh còn lại)
Chọn C. 2cm; 3cm; 4cm

\(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}=\dfrac{180^0-\widehat{A}}{2}=\dfrac{180^0-80^0}{2}=\dfrac{100^0}{2}=50^0\)
Chọn C

\(x^2-6x+15=x^2-6x+9+6=\left(x-3\right)^2+6>=6\forall x\)
=>\(D=\dfrac{4}{x^2-6x+15}=\dfrac{4}{\left(x-3\right)^2+6}< =\dfrac{4}{6}=\dfrac{2}{3}\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3


TH1: x<=4/3
B=4-3x+3-2x+2-x=-6x+9
x<=4/3 mà x nguyên
nên \(x\in\left\{...;0;1\right\}\)
B=-6x+9 nên hàm số nghịch biến trên R
=>Khi x tăng thì y giảm
Khi x=0 thì \(B=-6\cdot0+9=9\)
TH2: 4/3<=x<=3/2
\(B=2-x+3-2x+3x-4=1\)
TH3: 3/2<=x<=2
\(B=2-x+3-2x+4-3x=-6x+9\)
B=-6x+9 nên hàm số B=-6x+9 nghịch biến trên R
3/2<=x<=2 mà x nguyên nên x=2
=>\(B=-6\cdot2+9=-12+9=-3\)
TH4: x>=2
\(B=x-2+2x-3+3x-4=6x-9\)
B=6x-9 nên B đồng biến trên R
=>Khi x=2 thì B=6x-9 nhỏ nhất trong khoảng \([2;+\infty)\)
=>B=6*2-9=3
Vậy: \(B_{min}=-3\) khi x=2

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
=>\(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)
nên DA<DC
c: Sửa đề: AE là phân giác của góc CAH
Ta có: \(\widehat{BAE}+\widehat{CAE}=\widehat{BAC}=90^0\)
\(\widehat{BEA}+\widehat{HAE}=90^0\)(ΔHAE vuông tại H)
mà \(\widehat{BAE}=\widehat{BEA}\)(ΔBAE cân tại B)
nên \(\widehat{CAE}=\widehat{HAE}\)
=>AE là phân giác của góc HAC
A) Ta có:
- BE = BA (theo giả thiết)
- AB = BD (do BD là phân giác của tam giác ABC)
- Góc ABD = góc EBD (do cùng chung góc tại B)
Vậy, tam giác ABD cân với tam giác EBD theo định lý cơ bản về tam giác cân.
B) Ta có:
- Tam giác ABD và tam giác CBD cùng chung cạnh BD và cùng chung góc tại D.
- AB = BC (do BD là phân giác của tam giác ABC)
Vậy, theo định lý cơ bản về tam giác cân, ta có AD = CD.
C) Ta có:
- Tam giác ABD và tam giác CBD cùng chung cạnh BD và cùng chung góc tại D.
- AB = BC (do BD là phân giác của tam giác ABC)
Vậy, theo định lý cơ bản về tam giác cân, ta có góc BAD = góc BCD. Do đó, AD là tia phân giác của góc CAD, tức là góc CAH.

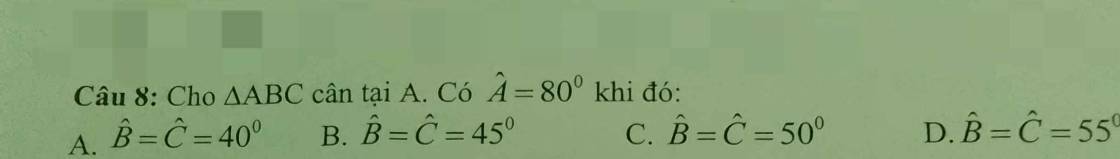


\(E=\dfrac{3x^2-6x+17}{x^2-2x+3}=\dfrac{3x^2-6x+9+8}{x^2-2x+3}\)
\(=3+\dfrac{8}{x^2-2x+3}\)
\(=3+\dfrac{8}{x^2-2x+1+2}=3+\dfrac{8}{\left(x-1\right)^2+2}\)
\(\left(x-1\right)^2+2>=2\forall x\)
=>\(\dfrac{8}{\left(x-1\right)^2+2}< =\dfrac{8}{2}=4\forall x\)
=>\(E=3+\dfrac{8}{\left(x-1\right)^2+2}=4+3=7\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1