a,\(\dfrac{-3}{21}\)+\(\dfrac{-2}{7}\)+\(\dfrac{1}{3}\)
b,\(\dfrac{-13}{15}\)+\(\dfrac{5}{-18}\)+\(\dfrac{4}{9}\)
c,\(\dfrac{-2}{5}\)-(\(\dfrac{-3}{11}\))
d,(-4)-(\(\dfrac{-4}{5}\))-\(\dfrac{2}{3}\)
e,\(\dfrac{3}{5}\)+(\(\dfrac{-4}{3}\))-\(\dfrac{-3}{4}\)
g,\(\dfrac{5}{8}\)-(-\(\dfrac{2}{5}\))-\(\dfrac{3}{10}\)
h,\(\dfrac{3}{4}\)-(-\(\dfrac{5}{3}\))+(\(\dfrac{1}{12}\)+\(\dfrac{2}{9}\))



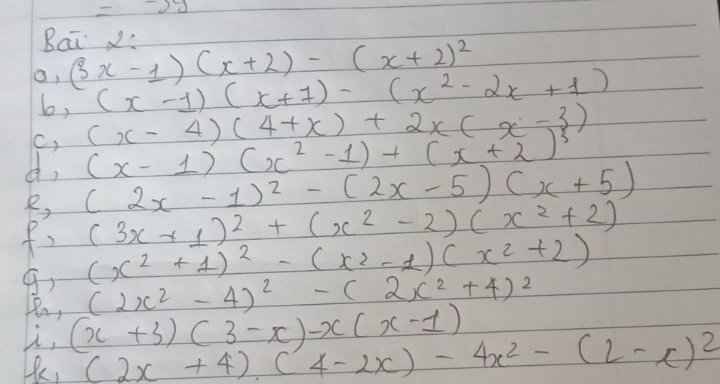

 giup em bai nay a kho qua
giup em bai nay a kho qua
a) \(\dfrac{-3}{21}+\dfrac{-2}{7}+\dfrac{1}{3}=\dfrac{-3}{21}+\dfrac{-6}{21}+\dfrac{7}{21}=-\dfrac{2}{21}\)
b) \(\dfrac{-13}{15}+\dfrac{5}{-18}+\dfrac{4}{9}=\dfrac{-78}{90}+\dfrac{-25}{90}+\dfrac{40}{90}=\dfrac{63}{90}=\dfrac{7}{10}\)
c) \(\dfrac{-2}{5}-\left(\dfrac{-3}{11}\right)=\dfrac{-2}{5}+\dfrac{3}{11}=\dfrac{-22}{55}+\dfrac{15}{55}=\dfrac{-7}{55}\)
d) \(\left(-4\right)-\left(\dfrac{-4}{5}\right)-\dfrac{2}{3}=\left(-4\right)+\dfrac{4}{5}-\dfrac{2}{3}=\dfrac{-60}{15}+\dfrac{12}{15}-\dfrac{10}{15}=\dfrac{-58}{15}\)
e) \(\dfrac{3}{5}+\left(\dfrac{-4}{3}\right)-\dfrac{-3}{4}=\dfrac{3}{5}+\left(\dfrac{-4}{3}\right)+\dfrac{3}{4}=\dfrac{36}{60}+\dfrac{-80}{60}+\dfrac{45}{60}=\dfrac{1}{60}\)
g) \(\dfrac{5}{8}-\left(-\dfrac{2}{5}\right)-\dfrac{3}{10}=\dfrac{5}{8}+\dfrac{2}{5}-\dfrac{3}{10}=\dfrac{25}{40}+\dfrac{16}{40}-\dfrac{12}{40}=\dfrac{29}{40}\)
h) \(\dfrac{3}{4}-\left(-\dfrac{5}{3}\right)+\left(\dfrac{1}{12}+\dfrac{2}{9}\right)=\dfrac{3}{4}+\dfrac{5}{3}+\left(\dfrac{3}{36}+\dfrac{8}{36}\right)=\dfrac{27}{36}+\dfrac{60}{36}+\dfrac{11}{36}=\dfrac{98}{36}=\dfrac{49}{18}\)
a) \(\dfrac{-3}{21}+\dfrac{-2}{7}+\dfrac{1}{3}=\dfrac{-3}{21}-\dfrac{6}{21}+\dfrac{7}{21}\\ =\dfrac{-3-6+7}{21}=-\dfrac{2}{21}\)
b) \(\dfrac{-13}{15}+\dfrac{5}{-18}+\dfrac{4}{9}=\dfrac{-78}{90}-\dfrac{25}{90}+\dfrac{40}{90}\\ =\dfrac{-78-25+40}{90}=\dfrac{-63}{90}=-\dfrac{7}{10}\)
c) \(\dfrac{-2}{5}-\left(\dfrac{-3}{11}\right)=-\dfrac{2}{5}+\dfrac{3}{11}\\ =-\dfrac{22}{55}+\dfrac{15}{55}=-\dfrac{7}{55}\)