Lời giải:

\(A=\frac{\sqrt{x}(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}+\frac{\sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}+3)}-\frac{4\sqrt{x}-6}{(\sqrt{x}-3)(\sqrt{x}+3)}\\ =\frac{\sqrt{x}(\sqrt{x}-3)+\sqrt{x}+3-(4\sqrt{x}-6)}{(\sqrt{x}-3)(\sqrt{x}+3)}\\ =\frac{x-6\sqrt{x}+9}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{(\sqrt{x}-3)^2}{(\sqrt{x}-3)(\sqrt{x}+3)}\\ =\frac{\sqrt{x}-3}{\sqrt{x}+3}\)

\(A=\dfrac{2021x+2022\sqrt{1-x^2}+2023}{\sqrt{1-x^2}}\)

\(A=2022+\dfrac{2021x+2023}{\sqrt{1-x^2}}\)

Xét \(\dfrac{2021x+2023}{\sqrt{1-x^2}}\)

\(\dfrac{2021x+2023}{\sqrt{1-x^2}}\ge2\sqrt{2022}\) 

\(\Rightarrow A\ge2022+2\sqrt{2022}\)

\(A\ge2\left(1011+\sqrt{2022}\right)\)

Dấu "=" xảy ra khi \(x=-\dfrac{2021}{2023}\)

\(\left\{{}\begin{matrix}8x^3y^3+27=18y^3\left(1\right)\\4x^2y+6x=y^2\left(2\right)\end{matrix}\right.\)

pt (2) \(\Leftrightarrow4x^2y^2+6xy=y^3\) (3)

Thế (3) vào (1), ta được \(8x^3y^3+27=18\left(4x^2y^2+6xy\right)\)

\(\Leftrightarrow8\left(xy\right)^3-72\left(xy\right)^2-108xy+27=0\) (4)

Đặt \(xy=t\) thì (4) thành

\(8t^3-72t^2-108t+27=0\)

\(\Leftrightarrow8t^3+12t^2-84t^2-126t+18t+27=0\)

\(\Leftrightarrow4t^2\left(2t+3\right)-42t\left(2t+3\right)+9\left(2t+3\right)=0\)

\(\Leftrightarrow\left(2t+3\right)\left(4t^2-42t+9\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=-\dfrac{3}{2}\\t=\dfrac{21\pm9\sqrt{5}}{4}\end{matrix}\right.\)

Xét \(t=-\dfrac{3}{2}\) \(\Rightarrow xy=-\dfrac{3}{2}\) . Thay vào (2), ta có:

\(y^3=4\left(xy\right)^2+6xy\) \(=4\left(-\dfrac{3}{2}\right)^2+6\left(-\dfrac{3}{2}\right)=0\)  

\(\Leftrightarrow y=0\) \(\Leftrightarrow x=0\)

Nếu \(t=\dfrac{21+9\sqrt{5}}{4}\) thì \(xy=\dfrac{21+9\sqrt{5}}{4}\). Thay vào (2), ta có:

\(y^3=4\left(\dfrac{21+9\sqrt{5}}{4}\right)^2+6\left(\dfrac{21+9\sqrt{5}}{4}\right)\) \(\Rightarrow y=...\Rightarrow x=...\)

Xét tương tự với \(t=\dfrac{21-9\sqrt{5}}{4}\)

Vậy ...

 Với lại bạn cần loại nghiệm \(x=y=0\) nhé vì nó không thỏa mãn pt (1).

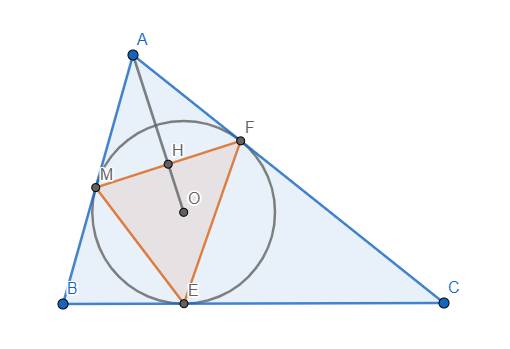
Gọi H là giao điểm của FM và OA.

Tính được \(AM=\dfrac{b+c-a}{2}\)

Tính được \(cos\widehat{BAC}=\dfrac{b^2+c^2-a^2}{2bc}\) rồi dùng 

\(MF=\sqrt{AM^2+AF^2-2AM.AF.cos\widehat{BAC}}\)

 \(=\sqrt{2AM^2\left(1-cos\widehat{BAC}\right)}\) 

 \(=MA\sqrt{2\left(1-\dfrac{b^2+c^2-a^2}{2bc}\right)}\)

 \(=MA\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}\)

 \(=\dfrac{b+c-a}{2}\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}\)

\(\Rightarrow\dfrac{MF}{MA}=\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}=J\)

\(\Rightarrow cos\widehat{MEF}=cos\widehat{MAH}=\dfrac{MH}{MA}=\dfrac{J}{2}\)

\(\Rightarrow sin\widehat{MEF}=\sqrt{1-cos^2\widehat{MAH}}\)

 \(=\sqrt{1-\dfrac{J^2}{4}}\) 

 \(=\sqrt{1-\dfrac{a^2-b^2-c^2+2bc}{4bc}}\)

 \(=\sqrt{\dfrac{\left(b+c\right)^2-a^2}{4bc}}\) \(=A\)

Ta cũng tính được \(ME=\dfrac{c+a-b}{2}\sqrt{\dfrac{b^2-\left(c-a\right)^2}{ca}}=\dfrac{c+a-b}{2}\sqrt{\dfrac{\left(b+c-a\right)\left(a+b-c\right)}{ca}}\)

\(EF=\dfrac{a+b-c}{2}\sqrt{\dfrac{c^2-\left(a-b\right)^2}{ab}}=\dfrac{a+b-c}{2}\sqrt{\dfrac{\left(c+a-b\right)\left(b+c-a\right)}{ab}}\)

\(\Rightarrow S_{MEF}=\dfrac{1}{2}EM.EF.sin\widehat{MEF}\) \(=...\)

 Điểm F ở câu a) với điểm N ở câu b) là những điểm gì thế bạn? Mình thấy trong đề không có định nghĩa các điểm này.

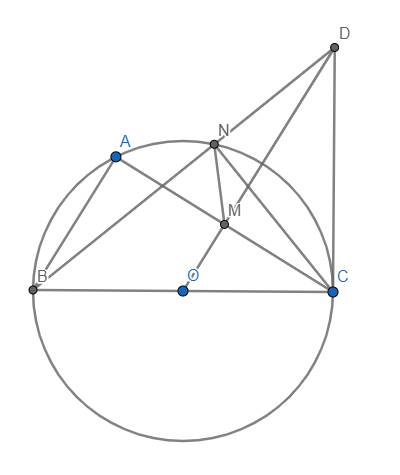
a) Xét đường tròn (O) có OM vuông góc với dây cung AC tại M 

\(\Rightarrow\) M là trung điểm AC 

\(\Rightarrow MA=MC=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)

Tam giác OCM vuông tại M nên \(OM=\sqrt{OC^2-MC^2}\) \(=\sqrt{5^2-3^2}\) \(=4\left(cm\right)\) 

b) Vì DC là tiếp tuyến tại C của (O) nên \(CD\perp OC\) hay \(\Delta OCD\) vuông tại C

 Xét \(\Delta OCD\) vuông tại C có đường cao CM nên \(DC^2=DM.DO\) (hệ thức lượng trong tam giác vuông)

c) Xét đường tròn (O) có đường kính BC nên \(\widehat{BNC}=90^o\) hay \(CN\perp BD\) tại N.

 Xét tam giác BCD vuông tại C có đường cao CN nên \(DC^2=DN.DB\)

 Từ đó suy ra \(DM.DO=DN.DB\left(=DC^2\right)\) \(\Rightarrow\dfrac{DM}{DB}=\dfrac{DN}{DO}\)

 Xét \(\Delta DMN\) và \(\Delta DBO\), có:

 \(\widehat{BDO}\) chung, \(\dfrac{DM}{DB}=\dfrac{DN}{DO}\)

 \(\Rightarrow\Delta DMN~\Delta DBO\left(c.g.c\right)\)

 \(\Rightarrow\widehat{DMN}=\widehat{NBO}\)

Lại có \(\widehat{DMN}+\widehat{NMO}=180^o\)

\(\Rightarrow\) đpcm