ĐKXĐ: x>0; x<>9

a:\(P=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{3}{x\sqrt{x}-9\sqrt{x}}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{3\sqrt{x}-3}{x+3\sqrt{x}}\right)\)

\(=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{3}{\sqrt{x}\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{3\sqrt{x}-3}{\sqrt{x}\left(\sqrt{x}+3\right)}\right)\)

\(=\dfrac{x-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\cdot\sqrt{x}}:\dfrac{x-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\cdot\sqrt{x}}\)

\(=\dfrac{x-3\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x-3\sqrt{x}+3}=\dfrac{1}{\sqrt{x}-3}\)

b: P>1

=>P-1>0

=>\(\dfrac{1-\sqrt{x}+3}{\sqrt{x}-3}>0\)

=>\(\dfrac{4-\sqrt{x}}{\sqrt{x}-3}>0\)

=>\(\dfrac{\sqrt{x}-4}{\sqrt{x}-3}< 0\)

=>\(3< \sqrt{x}< 4\)

=>9<x<16

Thời gian người đi xe máy từ nhà đến trường là:

`10` giờ `30` phút `-8` giờ `=2` giờ `30` phút `=2,5` giờ

Vận tốc của người đi xe máy là:

`v = S/t = 150/(2,5)=60 (km`/`h)`

Đáp số: `60 km`/`h`

a: \(P=\left(\dfrac{2\sqrt{xy}}{x-y}-\dfrac{\sqrt{x}+\sqrt{y}}{2\sqrt{x}-2\sqrt{y}}\right)\cdot\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)

\(=\left(\dfrac{2\sqrt{xy}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}-\dfrac{\sqrt{x}+\sqrt{y}}{2\left(\sqrt{x}-\sqrt{y}\right)}\right)\cdot\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)

\(=\dfrac{4\sqrt{xy}-\left(\sqrt{x}+\sqrt{y}\right)^2}{2\cdot\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\cdot\dfrac{2\sqrt{x}}{\left(\sqrt{x}-\sqrt{y}\right)}\)

\(=\dfrac{-x+2\sqrt{xy}-y}{\left(\sqrt{x}-\sqrt{y}\right)^2}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}=\dfrac{-\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)^2}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)

\(=-\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)

b: \(\dfrac{x}{y}=\dfrac{4}{9}\)

=>\(\dfrac{x}{4}=\dfrac{y}{9}=k\)

=>x=4k; y=9k

\(P=\dfrac{-\sqrt{x}}{\sqrt{x}+\sqrt{y}}=\dfrac{-\sqrt{4k}}{\sqrt{4k}+\sqrt{9k}}=\dfrac{-2\sqrt{k}}{2\sqrt{k}+3\sqrt{k}}=-\dfrac{2}{5}\)

a) Gọi x là số đo cung nhỏ AB (x > 0)

Số đo cung lớn AB là 3x

Ta có:

x + 3x = 360⁰

4x = 360⁰

x = 360⁰ : 4

x = 90⁰

Vậy số đo cung nhỏ AB là 90⁰

Số đo cung lớn AB là 3.90⁰ = 270⁰

b)

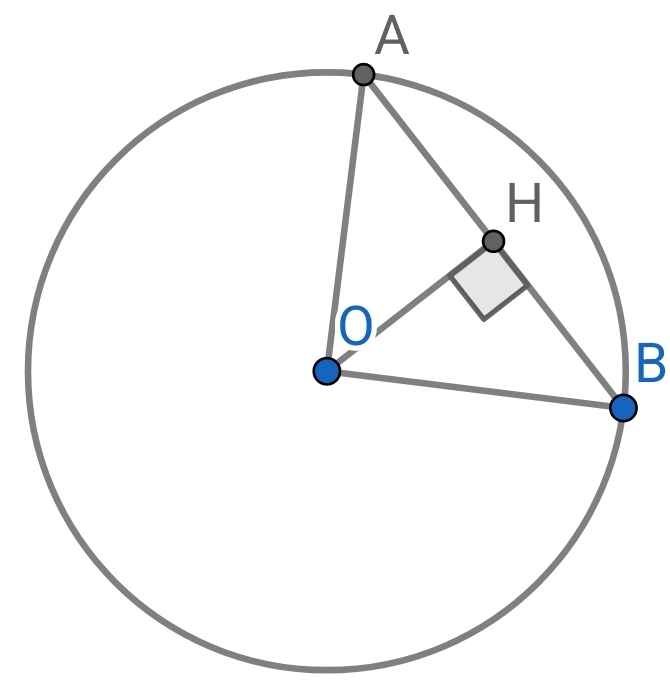
Do số đo cung nhỏ AB là 90⁰ (cmt)

⇒ ∠AOB = 90⁰

⇒ ∆AOB vuông tại O

Do OH là khoảng cách từ O đến AB

⇒ OH ⊥ AB

⇒ H là trung điểm của AB

⇒ OH là đường trung tuyến ứng với cạnh huyền AB của ∆AOB vuông tại O

⇒ OH = AB : 2

Gọi x là số đo cung nhỏ AB (x > 0)

Số đo cung lớn AB là 2x

Ta có:

x + 2x = 360⁰

3x = 360⁰

x = 360⁰ : 3

x = 120⁰

⇒ ∠AOB = 120⁰

∆AOB có:

OA = OB = R

⇒ ∆AOB cân tại O

⇒ ∠OAB = ∠OBA = (180⁰ - ∠AOB) : 2

= (180⁰ - 120⁰) : 2

= 30⁰

Ta có hình vẽ sau:

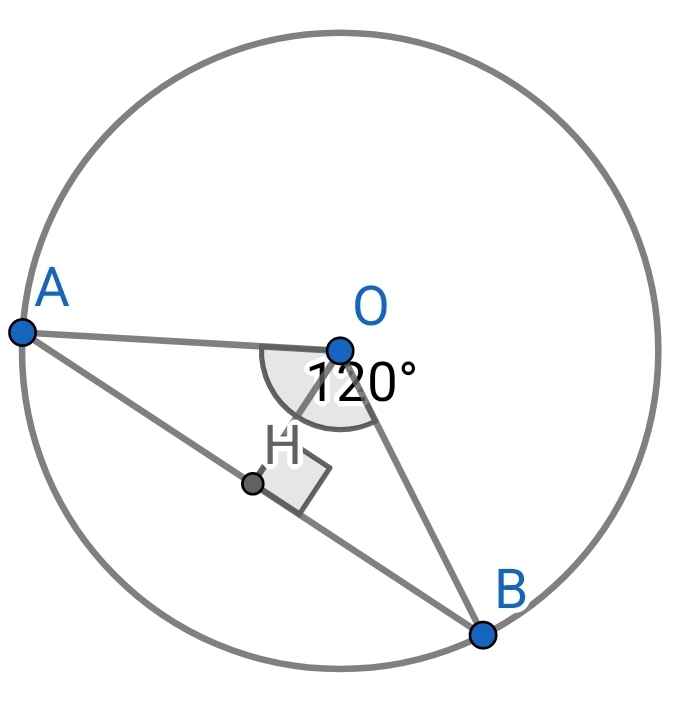
Vẽ đường cao OH của ∆OAB

⇒ ∆OAH vuông tại H

⇒ cosOAH = AH : OA

⇒ AH = OA.cosOAH

= R.cos30⁰

Do OH ⊥ AB

⇒ H là trung điểm của AB

⇒ AB = 2AH

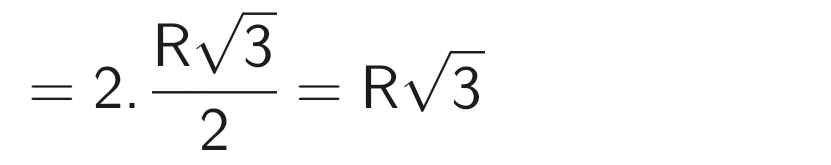
Ta có: \(\widehat{ABC}=90^0\)

=>B nằm trên đường tròn đường kính AC(1)

Ta có: \(\widehat{ADC}=90^0\)

=>D nằm trên đường tròn đường kính AC(2)

Từ (1),(2) suy ra B,D cùng nằm trên đường tròn đường kính AC

=>A,B,C,D cùng thuộc đường tròn tâm O, đường kính AC

Xét (O) có

AC là đường kính

BD là dây

Do đó: BD<AC

Xét tứ giác BC'B'C có \(\widehat{BC'C}=\widehat{BB'C}=90^0\)

nên BC'B'C là tứ giác nội tiếp đường tròn đường kính BC

=>BC'B'C là tứ giác nội tiếp đường tròn tâm O, đường kính BC

Xét (O) có

BC là đường kính

B'C' là dây

Do đó: B'C'<BC

Gọi OH là khoảng cách từ O đến dây MN

=>OH\(\perp\)MN tại H

ΔOMN cân tại O

mà OH là đường cao

nên H là trung điểm của MN

=>\(HM=HN=\dfrac{R}{2}\)

ΔOHM vuông tại H

=>\(OH^2+HM^2=OM^2\)

=>\(OH^2=R^2-\left(\dfrac{R}{2}\right)^2=\dfrac{3R^2}{4}\)

=>\(OH=\sqrt{\dfrac{3R^2}{4}}=\dfrac{R\sqrt{3}}{2}\)

=>Khoảng cách từ O đến dây MN là \(\dfrac{R\sqrt{3}}{2}\)

Gọi giao điểm của MN với OA là H

Vì MN\(\perp\)OA tại trung điểm của OA

nên MN\(\perp\)OA tại H và H là trung điểm của OA

Xét ΔOMA có 

MH là đường cao

MH là đường trung tuyến

Do đó: ΔOMA cân tại M

=>MO=MA

mà OM=OA

nên OM=MA=OA

=>ΔOMA đều

=>\(\widehat{MOA}=60^0\)

Xét ΔMHO vuông tại H có \(sinMOH=\dfrac{MH}{MO}\)

=>\(\dfrac{MH}{10}=sin60=\dfrac{\sqrt{3}}{2}\)

=>\(MH=10\cdot\dfrac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)

ΔOMN cân tại O

mà OH là đường cao

nên H là trung điểm của MN

=>\(MN=2\cdot MH=2\cdot5\sqrt{3}=10\sqrt{3}\left(cm\right)\)

Lời giải:
Giả sử mỗi người ăn 1 suất gạo/ ngày

Sau 10 ngày, đơn vị còn số suất gạo là:

$750\times (50-10)\times 1=30000$ (suất)

Tổng số người trong đơn vị sau khi bổ sung thêm người là:
$30000:25:1=1200$ (người)

Số người đến thêm:

$1200-750=450$ (người)

xắp xếp các số0,15,5,14,2,35,1,075,1,1 theo thứ tự từ bé đến lớn