




Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Để ý rằng phương trình của trục Ox là \(y=0\). Do đó pt hoành độ giao điểm của Ox và d là \(\left(m^2+1\right)x_A-2m=0\Leftrightarrow x_A=\dfrac{2m}{m^2+1}\)
Mà \(OA=\left|x_A\right|=\left|\dfrac{2m}{m^2+1}\right|=\dfrac{2\left|m\right|}{m^2+1}\) , \(OA=\dfrac{4}{5}\)
\(\Rightarrow\dfrac{2\left|m\right|}{m^2+1}=\dfrac{4}{5}\)
\(\Leftrightarrow2m^2-5\left|m\right|+2=0\)
Xét \(m\ge0\), khi đó \(2m^2-5m+2=0\Leftrightarrow\left[{}\begin{matrix}m=2\\m=\dfrac{1}{2}\end{matrix}\right.\) (nhận)
Xét \(m< 0\), khi đó \(2m^2+5m+2=0\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{1}{2}\\m=-2\end{matrix}\right.\) (nhận)
Vậy \(m\in\left\{\pm2;\pm\dfrac{1}{2}\right\}\) thỏa mãn ycbt.
c) Theo câu b), ta có \(OA=\dfrac{2\left|m\right|}{m^2+1}\). d cắt Oy tại \(B\left(0,-2m\right)\)
\(\Rightarrow OB=\left|-2m\right|=2\left|m\right|\)
Có \(OA=2OB\Leftrightarrow\dfrac{2\left|m\right|}{m^2+1}=4\left|m\right|\)
\(\Leftrightarrow\left|m\right|\left(2-\dfrac{1}{m^2+1}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\2m^2+1=0\left(vôlý\right)\end{matrix}\right.\)
Vậy \(m=0\) thỏa mãn ycbt.
d) Gọi \(h\) là khoảng cách từ O đến d thì khi đó:
\(\dfrac{1}{h^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
\(=\dfrac{1}{\left(\dfrac{2\left|m\right|}{m^2+1}\right)^2}+\dfrac{1}{\left(2\left|m\right|\right)^2}\)
\(=\dfrac{m^4+2m^2+1}{4m^2}+\dfrac{1}{4m^2}\)
\(=\dfrac{m^4+2m^2+2}{4m^2}\)
\(\Rightarrow h^2=\dfrac{4m^2}{m^4+2m^2+2}\)
Đặt \(t=m^2\left(t>0\right)\) thì ta có \(h^2=\dfrac{4t}{t^2+2t+2}=P\)
\(\Leftrightarrow Pt^2+2\left(P-2\right)t+2P=0\) (*)
Có \(\Delta'=\left(P-2\right)^2-2P^2=P^2-4P+4-2P^2=-P^2-4P+4\)
\(\Delta'\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Ta thấy \(P=\dfrac{2P}{P}=2>0\) nên để pt đã cho có 1 nghiệm dương thì \(S>0\Leftrightarrow-2\left(P-2\right)>0\Leftrightarrow P< 2\)
Kết hợp 2 điều kiện, ta được \(-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(maxP=-2+2\sqrt{2}\). Dấu "=" xảy ra khi \(t=\dfrac{-2\left(-2+2\sqrt{2}-2\right)}{2\left(-2+2\sqrt{2}\right)}=\sqrt{2}\)
\(\Leftrightarrow m^2=\sqrt{2}\Leftrightarrow m=\pm\sqrt[4]{2}\)
Vậy \(m=\pm\sqrt[4]{2}\) thỏa mãn ycbt.

a: \(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\9x+3y=27\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+3y-x-3y=27-11\\x+3y=11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x=16\\3y=11-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{11-x}{3}=\dfrac{11-2}{3}=\dfrac{9}{3}=3\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+10y-3x=-1\\2x+4-3x+15y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y=-1\\-x+15y=-16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\-2x+30y=-32\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y-2x+30y=-1+\left(-32\right)\\x-15y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}40y=-33\\x=15y+16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=15\cdot\dfrac{-33}{40}+16=\dfrac{29}{8}\end{matrix}\right.\)
a)
\(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+9y=33\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}8y=24\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\3x+3=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3\\x=\dfrac{6}{3}=2\end{matrix}\right.\)
b)
\(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x+10y=3x-1\\2x+4=3x-15y-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\2x-30y=32\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}40y=-33\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x+\dfrac{99}{8}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=16-\dfrac{99}{8}=\dfrac{29}{8}\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x+2y=1+3\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\7y=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2=4\\y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=4-2=2\\y=1\end{matrix}\right.\)
Vậy: ...
\(\left\{{}\begin{matrix}x+2y=1+3\\2x-3y=1\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x+4y-\left(2x-3y\right)=8-1\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x+4y-2x+3y=7\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\\left(2x-2x\right)+\left(4y+3y\right)=7\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\0+7y=7\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2x+4y=8\\y=1\end{matrix}\right.\)
Thay y = 1 vào biểu thức 2\(x\) + 4y = 8 ta có: 2\(x\) + 4.1 = 8
⇒ 2\(x\) + 4 = 8 ⇒ 2\(x\) = 4 ⇒ \(x\) = 4: 2 ⇒ \(x\) = 2
Vậy \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Nửa chu vi của hình chữ nhật là: 60:2=30(m)
Chiều rộng của hình chữ nhật là: (30-6):2=12(m)
Chiều dài của hình chữ nhật là: 30 - 12 = 18(m)
Diện tích mảnh đất là: 18 x 12 = 216 (m2)
Đáp số: 216m2
Giải:
Nửa chu vi của mảnh vườn hình chữ nhật là:
60 : 2 = 30 (m)
Gọi chiều rộng lúc đầu của mảnh vườn hình chữ nhật là \(x\) (m); 30 > \(x\) > 0
Chiều dài lúc đầu của mảnh vườn hình chữ nhật là: 30 - \(x\) (m)
Chiều dài của mảnh vườn hình chữ nhật lúc sau là:
30 - \(x\) + 2 = (30 + 2) - \(x\) = 32 - \(x\) (m)
Chiều rộng của hình chữ nhật lúc sau là: \(x\) + 6 (m)
Diện tích của hình chữ nhật lúc sau là:
(32 - \(x\))(\(x\) + 6) (m2)
Diện tích của mảnh vườn hình chữ nhật lúc đầu là: (30 - \(x\)) x \(x\) = 30\(x\) - \(x^2\) (m2)
Theo bài ra ta có phương trình:
(32 - \(x\))(\(x\) + 6) - (30\(x\) - \(x^2\)) = 96
32\(x\) + 192 - \(x^2\) - 6\(x\) - 30\(x\) + \(x^2\) = 96
(32\(x\) - 6\(x\) - 30\(x\)) + 192 - (\(x^2\) - \(x^2\)) = 96
(26\(x\) - 30\(x\)) + 192 + 0 = 96
- 4\(x\) + 192 = 96
4\(x\) = 192 - 96
4\(x\) = 96
\(x\) = 96 : 4
\(x\) = 24
Chiều dài ban đầu của hình chữ nhật là: 30 - 24 = 6 (m)
6 < 24
Chiều dài nhỏ hơn chiều rộng, không có hình chữ nhật nào có kích thước thoả mãn đề bài.

a: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\) và \(MA\cdot MB=HM^2\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right);NA\cdot NC=NH^2\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\left(3\right);AB^2=BH\cdot BC;AC^2=CH\cdot BC\)
Từ (1) và (3) suy ra \(AM\cdot AB=HB\cdot HC\)
b: Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>\(HA^2=HM^2+HN^2\)
=>\(HB\cdot HC=MA\cdot MB+NA\cdot NC\)
d: \(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)
=>\(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
e: Xét ΔAHB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM=\dfrac{BH^2}{BA}\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(CN\cdot CA=CH^2\)
=>\(CN=\dfrac{CH^2}{CA}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(BC=\dfrac{AB\cdot AC}{AH}\)
\(BM\cdot CN\cdot BC=\dfrac{BH^2}{BA}\cdot\dfrac{CH^2}{CA}\cdot\dfrac{AB\cdot AC}{AH}\)
\(=\dfrac{BH^2}{AH}\cdot CH^2=\dfrac{\left(BH\cdot CH\right)^2}{AH}=\dfrac{AH^4}{AH}=AH^3\)
mà AH=MN(AMHN là hình chữ nhật)
nên \(BM\cdot CN\cdot BC=MN^3\)


6h40p=20/3 giờ
Gọi thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là a(giờ) và b(giờ)
(Điều kiện: a>0; b>0)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{a}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{b}\)(công việc)
Trong 1 giờ, hai người làm được: \(1:\dfrac{20}{3}=\dfrac{3}{20}\)(công việc)
Do đó, ta có: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\left(1\right)\)
Trong 5 giờ, người thứ nhất làm được: \(\dfrac{5}{a}\)(công việc)
Trong 8 giờ, người thứ hai làm được: \(\dfrac{8}{b}\)(công việc)
Nếu người thứ nhất làm trong 5 giờ, sau đó nghỉ và người thứ hai làm trong 8 giờ thì xong nên ta có: \(\dfrac{5}{a}+\dfrac{8}{b}=1\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\\\dfrac{5}{a}+\dfrac{8}{b}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{a}+\dfrac{5}{b}=\dfrac{3}{4}\\\dfrac{5}{a}+\dfrac{8}{b}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{a}+\dfrac{8}{b}-\dfrac{5}{a}-\dfrac{5}{b}=1-\dfrac{3}{4}\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{b}=\dfrac{1}{4}\\\dfrac{1}{a}=\dfrac{3}{20}-\dfrac{1}{b}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=12\\\dfrac{1}{a}=\dfrac{3}{20}-\dfrac{1}{12}=\dfrac{9}{60}-\dfrac{5}{60}=\dfrac{4}{60}=\dfrac{1}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=12\\a=15\end{matrix}\right.\left(nhận\right)\)
Vậy: thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là 15(giờ) và 12(giờ)
Gọi thời gian nếu làm riêng của người thứ nhất, người thứ hai để hoàn thành công việc lần lượt là $a,b$ (giờ; $a,b>0$)
Mỗi giờ người thứ nhất làm được: $\frac1a$ (công việc)
Mỗi giờ người thứ hai làm được: $\frac1b$ (công việc)
Vì hai người cùng làm việc thì trong 6 giờ 40 phút (= $\frac{20}{3}$ giờ) thì xong công việc nên ta có phương trình: $\frac{20}{3}(\frac 1a+\frac1b)=1$
$\Leftrightarrow \frac1a+\frac1b=\frac{3}{20}$ (1)
Vì nếu người thứ nhất làm riêng trong 5 giờ rồi người thứ hai tiếp tục làm nốt trong 8 giờ thì xong công việc nên ta có phương trình:
$\frac5a+\frac8b=1$ (2)
Từ (1) và (2) ta có hệ: $\begin{cases} \frac1a+\frac1b=\frac{3}{20} \\ \frac5a+\frac8b=1 \end{cases}$
Đặt $\frac 1a=u:\frac1b=v;(u,v>0)$
Khi đó hot trở thành: $\begin{cases} u+v=\frac{3}{20}\\ 5u+8v=1\end{cases} \Leftrightarrow \begin{cases} u=\frac{1}{15}\\v=\frac{1}{12}\end{cases}$
$\Rightarrow \begin{cases} \frac1a=\frac{1}{15}\\\frac1b=\frac{1}{12} \end{cases} \Rightarrow \begin{cases} a=15 (tm)\\b=12(tm) \end{cases}$
Vậy: ...
#$\mathtt{Toru}$


Gọi đường thẳng (d): y=ax+b(a\(\ne\)0) là đường thẳng đi qua hai điểm (2;0); (-1;-2)
Thay x=2 và y=0 vào (d), ta được:
\(a\cdot2+b=0\)(1)
Thay x=-1 và y=-2 vào (d), ta được:
\(a\cdot\left(-1\right)+b=-2\left(2\right)\)
Từ (1),(2) ta có hệ phương trình: \(\left\{{}\begin{matrix}2a+b=0\\-a+b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+b+a-b=0-\left(-2\right)\\b=-2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=2\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b=-2\cdot\dfrac{2}{3}=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{2}{3}x-\dfrac{4}{3}\)
=>\(\dfrac{2}{3}x-y=\dfrac{4}{3}\)
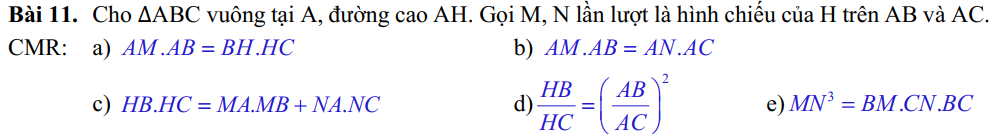


B5:
a) Thay x = 1 và y = 2 vào pt ta có:
\(m\cdot1+2-5=0\\ =>m-3=0\\ =>m=3\)
b) A(0;3) thuộc đường thẳng 4x - my - 6 = 0
=> Thay x = 0 và y = 3 vào đường thẳng ta có:
\(4\cdot0-m\cdot3-6=0\\ =>0-3m-6=0\\=> -3m-6=0\\ =>-3m=6\\ =>m=\dfrac{6}{-3}=-2\)
B11:
Ta có:
\(\left\{{}\begin{matrix}2x+3y=7\\x-3y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=6\\x-3y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{6}{3}=2\\2-3y=-1\end{matrix}\right. \Leftrightarrow\left\{{}\begin{matrix}x=2\\3y=2+1=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{3}{3}=1\end{matrix}\right.\)
=> Cặp (2;1) là nghiệm của hpt
B12:
Ta có
\(\left\{{}\begin{matrix}4x+5y=3\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+5y=3\\4x-12y=20\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-17}{17}=-1\\x+3=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=5-3=2\end{matrix}\right.\)
=> Cặp (2;-1) là nghiệm của hpt