\(20,23:0,125+60,69+89\times20,23\)

\(=20,23\times8+20,23\times3+20,23\times89\)

\(=20,23\left(8+3+89\right)=20,23\times100=2023\)

Lời giải:

Gọi $H$ là trung điểm của $AB$. Vì $SAB$ là tam giác đều nên $SH\perp AB$. Mà $AB=(SAB)\cap (ABCD)$ và $(SAB)\perp (ABCD)$

$\Rightarrow SH\perp (ABCD)$

Gọi $M$ là trung điểm $CD$ thì $HM\perp CD$. Mà $SH\perp CD$ (do $SH\perp (ABCD))$

$\Rightarrow (SHM)\perp CD$

$CD$ là giao tuyến của $(SCD), (ABCD)$

$\Rightarrow \angle ((SCD), (ABCD))=\angle (SM, HM)=\widehat{SMH}$

Tam giác $SHM$ vuông tại $H$ có:

$SH=\frac{\sqrt{3}}{2}AB = \frac{\sqrt{3}}{2}a$

$HM=AD=a$

$\Rightarrow \tan \widehat{SMH}=\frac{SH}{HM}=\frac{\sqrt{3}}{2}$

$\Rightarrow \angle ((SCD), (ABCD))=\widehat{SMH}\approx 41^0$

Câu 1: B

Vd1:

a: Vì SA\(\perp\)(ABC)

nên A là hình chiếu của S lên mp(ABC)

b: A là hình chiếu của S lên mp(ABC)

B là hình chiếu của B lên mp(ABC)

Do đó: AB là hình chiếu của SB lên mp(ABC)

Giúp mình câu 1 vs câu 2 với ạ mình cảm ơn

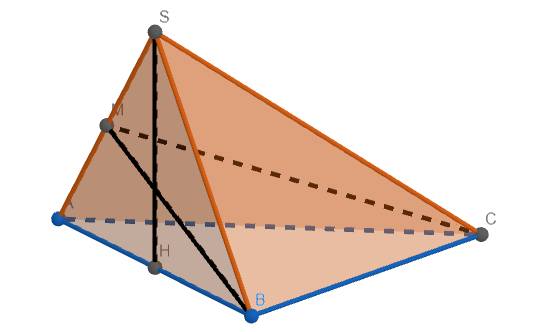
a) Gọi M là trung điểm SA. 

Có \(SH\perp\left(ABC\right)\Rightarrow SH\perp BC\).

Lại có \(BC\perp BA\) \(\Rightarrow BC\perp\left(SAB\right)\) \(\Rightarrow BC\perp SB\)

Do đó \(\widehat{\left(ABC\right),\left(SBC\right)}=\widehat{SBA}=60^o\)

Khi đó tam giác ABC đều \(\Rightarrow AB=BC=SB=SA=4\)

Đồng thời \(MB\perp SA\)

Mặt khác, ta thấy \(\Delta ABC=\Delta SBC\left(c.g.c\right)\) \(\Rightarrow SC=AC\)

\(\Rightarrow\Delta SAC\) cân tại C \(\Rightarrow MC\perp SA\)

Do đó \(\widehat{\left(SAC\right),\left(SAB\right)}=\widehat{BMC}\)

Vì \(BC\perp\left(SAB\right)\Rightarrow BC\perp BM\Rightarrow\Delta BCM\) vuông tại B

\(\Rightarrow\cos\widehat{BMC}=\dfrac{BC}{CM}=\dfrac{4}{\dfrac{4\sqrt{3}}{2}}=\dfrac{2\sqrt{3}}{3}\) 

Vậy \(\cos\widehat{\left(SAC\right),\left(SAB\right)}=\dfrac{2\sqrt{3}}{3}\)

Mình gửi trả lời rồi đó, bạn vào trang cá nhân của mình xem nhé.

 Bạn viết lại đề bài nhé, chứ nhìn vào mình không biết nó là \(\left(\dfrac{1}{3}\right)^{x^2}-2x-3=3^x+1\) hay \(\left(\dfrac{1}{3}\right)^{x^2-2x-3}=3^{x+1}\) hay cái gì khác nữa.

\(\left(\dfrac{1}{3}\right)^{x^2-2x-3}=3^{x+1}\)

=>\(3^{-x^2+2x+3}=3^{x+1}\)

=>\(-x^2+2x+3=x+1\)

=>\(-x^2+x+2=0\)

=>\(x^2-x-2=0\)

=>(x-2)(x+1)=0

=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)