Cho tam giác ABC, P là điểm bất kì trên BC. I, I1, I2 là tâm đường tròn nội tiếp tam giác ABC, APB, APC. Hạ ID vuông góc BC. Chứng minh rằng I1, I2, P, D cùng thuộc một đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\frac{3+\sqrt{5}}{\sqrt{10}+\sqrt{3+\sqrt{5}}}-\frac{3-\sqrt{5}}{\sqrt{10}+\sqrt{3-\sqrt{5}}}\)
\(A=\frac{3\sqrt{2}+\sqrt{10}}{2\sqrt{5}+\sqrt{6+2\sqrt{5}}}-\frac{3\sqrt{2}-\sqrt{10}}{2\sqrt{5}+\sqrt{6-2\sqrt{5}}}\)
\(A=\frac{3\sqrt{2}+\sqrt{10}}{2\sqrt{5}+\sqrt{\left(\sqrt{5}+1\right)^2}}-\frac{3\sqrt{2}-\sqrt{10}}{2\sqrt{5}+\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(A=\frac{3\sqrt{2}+\sqrt{10}}{2\sqrt{5}+\sqrt{5}+1}-\frac{3\sqrt{2}-\sqrt{10}}{2\sqrt{5}+\sqrt{5}-1}\)
\(A=\frac{3\sqrt{2}+\sqrt{10}}{3\sqrt{5}+1}-\frac{3\sqrt{2}-\sqrt{10}}{3\sqrt{5}-1}\)
\(A=\frac{\left(3\sqrt{2}+\sqrt{10}\right)\left(3\sqrt{5}-1\right)-\left(3\sqrt{2}-\sqrt{10}\right)\left(3\sqrt{5}+1\right)}{\left(3\sqrt{5}\right)^2-1}\)
\(A=\frac{90+3\sqrt{50}-3\sqrt{2}-\sqrt{10}-90+3\sqrt{50}-3\sqrt{2}+\sqrt{10}}{44}\)
\(A=\frac{6\sqrt{50}-6\sqrt{2}}{44}=\frac{\sqrt{2}\left(6\sqrt{25}-6\right)}{44}=\frac{24\sqrt{2}}{44}=\frac{6\sqrt{2}}{11}\)

a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\Rightarrow AC^2=BC^2-AB^2=25-9=16\Rightarrow AC=4\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{3.4}{5}=\frac{12}{5}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{9}{5}\)cm
-> CH = BC - BH = \(5-\frac{9}{5}=\frac{25-9}{5}=\frac{16}{5}\)cm
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH^2=CH.BH\Rightarrow BH=\frac{AH^2}{CH}=25\)cm
-> BC = BH + CH = \(25+144=169\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC=25.169=4225\Rightarrow AB=65\)cm
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\Rightarrow AC^2=BC^2-AB^2=24336\Rightarrow AC=156\)cm

\(a,x-\sqrt{x-4\sqrt{x}+4}=8\)
\(x-\sqrt{\left(\sqrt{x}-2\right)^2}=8\)
\(x-\left|\sqrt{x}-2\right|=8\)
\(TH1:0\le x\le2\)
\(x-2+\sqrt{x}=8\)
\(x+\sqrt{x}-10=0\)
\(\sqrt{\Delta}=1-\left(4.-10\right)=\sqrt{41}\)
\(\orbr{\begin{cases}x_1=\frac{\sqrt{41}-1}{2}\left(KTM\right)\\x_2=\frac{-\sqrt{41}-1}{2}\left(KTM\right)\end{cases}}\)
\(TH2:x>2\)
\(x-\sqrt{x}+2=8\)
\(x-\sqrt{x}-6=0\)
\(\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)=0\)
\(\orbr{\begin{cases}\sqrt{x}+2=0\\\sqrt{x}-3=0\end{cases}\orbr{\begin{cases}\sqrt{x}=-2\left(KTM\right)\\x=9\left(TM\right)\end{cases}}}\)
\(b,\sqrt{\frac{1}{4}x^2+x+1}-\sqrt{6-2\sqrt{5}}=0\)
\(\sqrt{\left(\frac{1}{2}x+1\right)^2}-\sqrt{\sqrt{5}^2-2\sqrt{5}+1}=0\)
\(\left|\frac{1}{2}x+1\right|-\sqrt{\left(\sqrt{5}-1\right)^2}=0\)
\(\left|\frac{1}{2}x+1\right|-\sqrt{5}+1=0\)
\(\left|\frac{1}{2}x+1\right|=\sqrt{5}-1\)
\(\orbr{\begin{cases}\frac{1}{2}x+1=\sqrt{5}-1\\\frac{1}{2}x+1=1-\sqrt{5}\end{cases}\orbr{\begin{cases}\frac{1}{2}x=\sqrt{5}-2\\\frac{1}{2}x=-\sqrt{5}\end{cases}\orbr{\begin{cases}x=2\sqrt{5}-4\\x=-2\sqrt{5}\end{cases}}}}\)
\(c,\sqrt{2x+4+6\sqrt{2x-5}}+\sqrt{2x-4-2\sqrt{2x-5}}=4\)
\(\sqrt{2x-5+6\sqrt{2x-5}+9}+\sqrt{2x-5-2\sqrt{2x-5}+1}=4\)
\(\sqrt{\left(\sqrt{2x-5}+3\right)^2}+\sqrt{\left(\sqrt{2x-5}+1\right)^2}=4\)
\(\left|\sqrt{2x-5}+3\right|+\left|\sqrt{2x-5}+1\right|=4\)
\(\sqrt{2x-5}+3+\sqrt{2x-5}+1=4\)
\(\sqrt{2x-5}=0\)
\(x=\frac{5}{2}\left(TM\right)\)

a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=9+16=25\Rightarrow BC=5\)cm
*Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{12}{5}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{9}{5}\)cm
-> CH = \(5-\frac{9}{5}=\frac{25-9}{5}=\frac{16}{5}\)cm
b, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH^2=BH.CH=9.16=144\Rightarrow AH=12\)cm
-> CH + BH = BC = 16 + 9 = 25
* Áp dụng hệ thức : \(AB^2=BH.BC=9.25=225\Rightarrow AB=15\)cm
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\Rightarrow AC^2=BC^2-AB^2=400\Rightarrow AC=20\)cm

Đặt \(\overline{ab}=x;\overline{cd}=y\Rightarrow\overline{abcd}=100\overline{ab}+\overline{cd}\)
\(=100x+y\left(10\le x\le99;y\ge0\right)\)
\(\Rightarrow100x+y=\left(x+y\right)^2\)
\(=x^2+2xy+y^2\left(1\right)\)
\(\Rightarrow x^2+\left(2y-100\right)x+\left(y^2-y\right)=0\left(2\right)\)
Để \(x,y\inℤ\)thoản mãn (1) \(\Rightarrow\left(2\right)\)có nghiệm nguyên
\(\Rightarrow\Delta'=\left(y-50\right)^2-\left(y^2-y\right)\)
\(=y^2-100y+2500-y^2+y\)
\(=-99y+2500\)
\(\Rightarrow\Delta'\ge0\Leftrightarrow2500-99y\ge0\)
\(\Rightarrow y\le25\)
(1) có nghiệm nguyên khi \(\sqrt{\Delta'}\)là số nguyên
\(\Rightarrow y\in\left\{0;1;25\right\}\)
\(\cdot y=0\Rightarrow\sqrt{\Delta'}=50\Rightarrow\orbr{\begin{cases}x_1=\left(50-y\right)+\sqrt{\Delta'}=50+50=100\\x_2=\left(50-y\right)-\sqrt{\Delta'}=50-50=0\end{cases}\left(loại\right)}\)
tính tương tự với y=1 ; y =25 nha cậu

Ta có:
\(A=\left(1+tan^2x\right)cos^2x-\left(1+cot^2x\right)\left(cos^2x-1\right)\)
\(=\frac{1}{cos^2x}.cos^2x-\frac{1}{sin^2x}.sin^2x\)
\(=1-1=0\)
\(B=tan72^o-cot18^o+sin^230^o+sin^260^o\)
\(=tan72^o-tan72^o+sin^230^o+cos^230^o\)
\(=1\)

e, Đặt \(A=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+2\sqrt{9-5}+3+\sqrt{5}=6+2.2=10\)

\(\frac{2xy^2}{3ab}\sqrt{\frac{9a^3b^4}{8xy^3}}=\frac{2xy^2}{3ab}\frac{3\sqrt{a^2.a}\sqrt{\left(b^2\right)^2}}{2\sqrt{2xy^2.y}}\)
\(=\frac{2xy^2}{3ab}\frac{3a\sqrt{a}b^2}{2y\sqrt{2xy}}=\frac{6xy^2ab^2\sqrt{a}}{6aby\sqrt{2xy}}=\frac{bxy\sqrt{a}}{\sqrt{2xy}}\)
\(=\frac{bxy\sqrt{2axy}}{2xy}=\frac{b\sqrt{2axy}}{2}\)

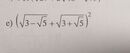
A B C D' E F P I I I 1 2 G
Gọi \(D'\) là điểm liên hợp đẳng giác với \(A\) trong \(\Delta II_1I_2\), \(IB\) giao \(DE\) tại \(G\)
Ta có \(\widehat{BGD}=\widehat{CDE}-\widehat{DBG}=90^0-\widehat{\frac{1}{2}ACB}-\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{BAC}=\widehat{IAE}\)
Suy ra \(\left(A,F,I,E,G\right)_{cyc}\) hay \(\widehat{IGA}=90^0\)
Vì \(\widehat{D'I_1I_2}=\widehat{GI_1A}\) và \(\widehat{I_1D'I_2}=180^0-\widehat{II_1A}-\widehat{II_2A}=180^0-\left(\widehat{BIC}-\frac{1}{2}\widehat{BAC}\right)=90^0\)
nên \(\Delta I_1GA~\Delta I_1D'I_2\), dẫn đến \(\Delta I_1D'G~\Delta I_1I_2A\)
Suy ra \(\widehat{I_1GD'}=\widehat{I_1AI_2}=\widehat{IAE}=180^0-\widehat{IGE}\), do đó \(\overline{E,G,D'}\) hay \(D'\in DE\)
Tương tự ta có \(D'\in DF\). Từ đó \(D\equiv D'\), suy ra \(\widehat{I_1DI_2}=\widehat{I_1D'I_2}=90^0=\widehat{I_1PI_2}\)
Vậy \(\left(I_1,I_2,P,D\right)_{cyc}.\)