Cho 0,5 mol potassium hidroxide KOH tác dụng hoàn toàn với hydrochloride acid HCl . Tính khối lượng muối thu được sau phản ứng >
( Cho K=39, Cl=35,5)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f=4/500
=> Tỷ lệ tần suất của biên cố E " một áo của nhà máy n không sản xuất đạt chât lượng" là 0.008.
Điều này có nghĩa là ước lượng xác suất để một chiếc áo bất kỳ từ nhà máy N không đạt chất lượng là 0.8% (tương đương với 0.008 trong hình thức thập phân)

a) Hàm số trên có:
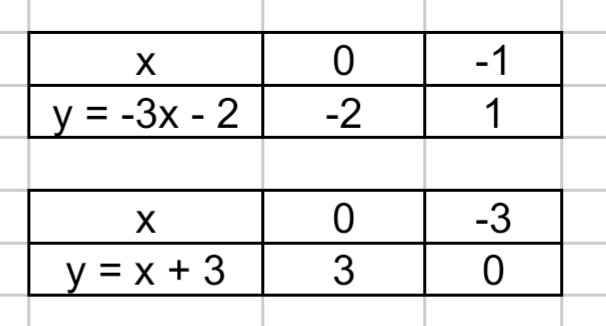
a = -3
b = -2
Đồ thị của hàm số cắt trục tung tại điểm (0; b) nên có tung độ là -2
b) Bảng giá trị:
Đồ thị:
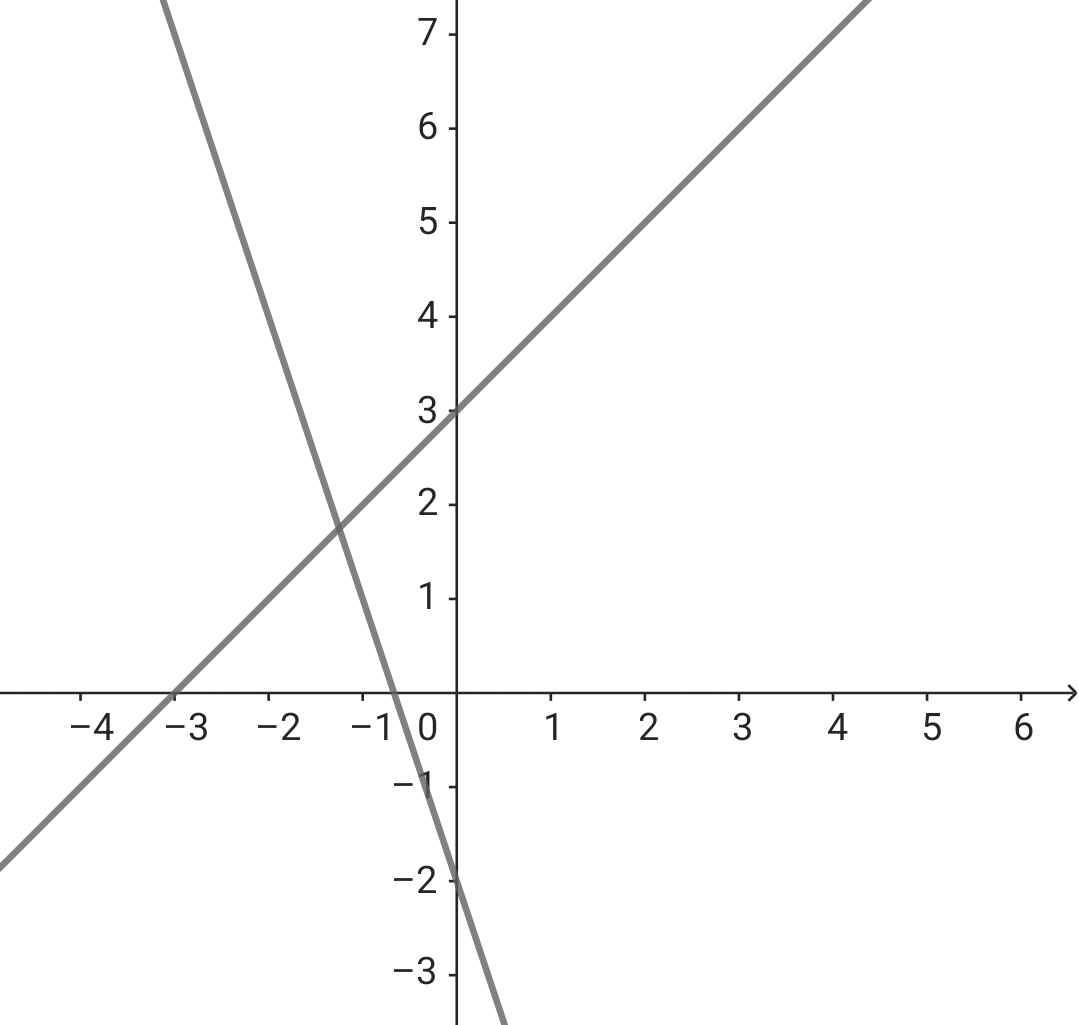
d) Phương trình hoành độ giao điểm của (d) và (d'):
-3x - 2 = x + 3
-3x - x = 3 + 2
-4x = 5
x = -5/4
y = -5/4 + 3 = 7/4
Vậy tọa độ giao điểm của (d) và (d') là (-5/4; 7/4)


Ta có x2 - y2= (x+y)(x-y) = 21(x-y) = 189
=> x-y= 189/21 = 9.
Giá trị x và y tmdk x-y=9 và x+y=21 là x=15, y=6

Gọi độ dài quãng đường AB là x(km)
(ĐK: x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{45}\left(giờ\right)\)
Thời gian đi từ B về A là \(\dfrac{x}{50}\left(giờ\right)\)
Tổng thời gian đi và về là:
1h30p-15p=1h15p=1,25(giờ)
Do đó, ta có phương trình:
\(\dfrac{x}{45}+\dfrac{x}{50}=1,25\)
=>\(\dfrac{10x+9x}{450}=1,25\)
=>19x=1,25*450=562,5
=>\(x=\dfrac{562.5}{19}=\dfrac{1125}{38}\left(nhận\right)\)
Vậy: Độ dài quãng đường AB là 1125/38 km

Gọi số sách ở ngăn 1 lúc đầu là x (quyển) và số sách ở ngăn 2 lúc đầu là y (quyển).
Theo đề bài, ta có:
Thay x = 2/3y vào phương trình thứ hai, ta được:
Thay y = 63 vào x = 2/3y, ta được:
Vậy số sách ở ngăn 1 lúc đầu là 42 quyển và số sách ở ngăn 2 lúc đầu là 63 quyển.

Gọi tuổi hiện nay của mẹ bạn Nam là: 3x
Phương trình biểu thị sự kiện sau 10 năm (3x+10)+(x+10)=76
Có (3x+10)+(x+10)=76
3x+10+x+10=76
4x+20=76
4x=56
x=14
Vậy tuổi của Nam là 14 tuổi và tuổi của mẹ Nam là 42 tuổi.
Vì mỗi năm tuổi mỗi người đều tăng 1 tuổi
=> Sau 10 năm tuổi mẹ Nam vẫn gấp 3 lần tuổi Nam
Gọi số tuổi Nam là a ( tuổi )
Sau 10 năm, tuổi của mẹ Nam là 3a+10
Sau 10 năm, tuổi của Nam là a+10
Theo bài ra, ta có:
\(\left(3a+10\right)+\left(a+10\right)=76\)
\(4a+20=76\)
\(4a=56\)
\(a=14\)
Vậy tuổi của Nam hiện nay là 14 tuổi

a: Xét ΔDBA vuông tại D và ΔABC vuông tại A có
\(\widehat{DBA}\) chung
Do đó: ΔDBA~ΔABC
b: ΔDBA~ΔABC
=>\(\dfrac{BD}{BA}=\dfrac{BA}{BC}\left(1\right)\)
Xét ΔBAD có BF là phân giác
nên \(\dfrac{BD}{BA}=\dfrac{FD}{FA}\left(2\right)\)
Xét ΔBAC có BE là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AE}{EC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{FD}{FA}=\dfrac{AE}{EC}\)
=>\(FD\cdot EC=AE\cdot FA\)
- Mol mass của KCl: 39 +35.3 =74.5 mol/g
-Khối lượng của KCl thu được = 0,5 mol x 74.5 mol/g = 37.25 g