cho đa thức p(x) = (2x-1)6 +(x-2)7=a7x7+a6x6+...+a1x+a0. hãy tính giá trị của T=a7+a6+...+a1+a0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đề bài, ta có \(\overline{qr}+2\overline{ppp}=2022\)
\(\Leftrightarrow\overline{ppp}=\dfrac{2022-\overline{qr}}{2}\) \(\ge\dfrac{2022-99}{2}=961,5\) hay \(\overline{ppp}\ge962\)
Do đó \(\overline{ppp}=999\)
Khi đó \(\overline{qr}=2022-2\overline{ppp}=2022-2.999=24\)
Vậy \(p=9,q=2,r=4\)

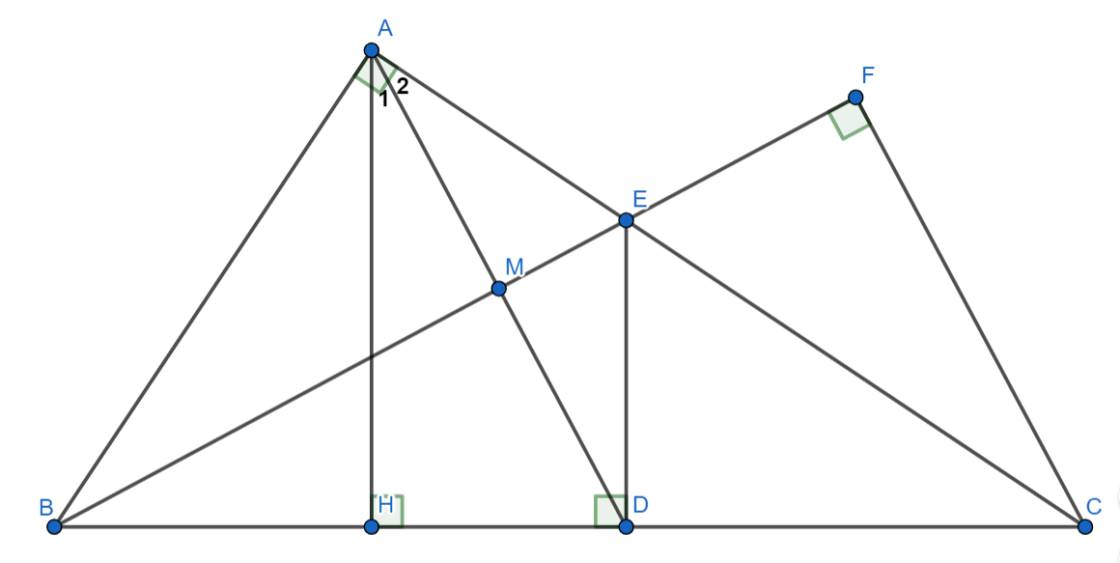
a) Xét \(\Delta BAE\) và \(\Delta BDE\) có:
\(\left\{{}\begin{matrix}\widehat{BAE}=\widehat{BDE}=90^{\circ}\left(\Delta ABC\text{ vuông tại }A;DE\perp BC\right)\\BE\text{ chung}\\BA=BD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta BAE=\Delta BDE\left(ch-cgv\right)\) (đpcm)
b) Ta có: \(BD=BA\Rightarrow B\) là điểm nằm trên đường trung trực của AD (1)
Vì \(\Delta BAE=\Delta BDE\left(cmt\right)\Rightarrow AE=DE\) (2 cạnh tương ứng)
\(\Rightarrow E\) là điểm nằm trên đường trung trực của AD (2)
Từ (1) và (2) \(\Rightarrow BE\) là đường trung trực của AD
Mà: \(BE\cap AD=\left\{M\right\}\) nên \(BM\perp AD\)
hay \(BM\) là đường cao của \(\Delta ABD\) (đpcm)
c) Vì \(AE=DE\Rightarrow\Delta ADE\) cân tại E (t/c)
\(\Rightarrow\widehat{A_2}=\widehat{EDA}\) (t/c) (3)
Lại có: \(\begin{cases} AH\perp CD\\ DE\perp CD \end{cases} \Rightarrow AH//DE\)
\(\Rightarrow\widehat{A_1}=\widehat{EDA}\) (2 góc so le trong) (4)
Từ (3) và (4) \(\Rightarrow\widehat{A_1}=\widehat{A_2}\)
Mà tia AD nằm trong \(\widehat{HAC}\)
nên tia AD là tia phân giác của \(\widehat{HAC}\) (đpcm)
d) Xét \(\Delta EBC\) có: \(\left\{{}\begin{matrix}AB\perp EC\left(\Delta ABC\text{ vuông tại }A;E\in AC\right)\\DE\perp BC\left(gt\right)\\CF\perp BE\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AB,DE,CF\) đồng quy (t/c) (đpcm)
$\text{#}Toru$

Đề là so sánh phân số mới đúng nhé bạn!
a)
Ta có:
Mẫu số chung 2 phân số: 12
$\frac{-3}{4}=\frac{-3\cdot3}{4\cdot3}=\frac{-9}{12}$
$\frac{-2}{3}=\frac{-2\cdot4}{3\cdot4}=\frac{-8}{12}$
Vì $-9<-8$ nên$\frac{-9}{12}<\frac{-8}{12}$
Vậy $\frac{-3}{4}<\frac{-2}{3}$
b)
$\frac{24}{-60}=\frac{24:-12}{-60:-12}=\frac{-2}{5}$
$\frac{-33}{44}=\frac{-33:11}{44:11}=\frac{-3}{4}$
Ta có:
Mẫu số chung 2 phân số: 20
$\frac{-2}{5}=\frac{-2\cdot4}{5\cdot4}=\frac{-8}{20}$
$\frac{-3}{4}=\frac{-3\cdot5}{4\cdot5}=\frac{-15}{20}$
Vì $-8>-15$ nên$\frac{-8}{20}>\frac{-15}{20}$
Vậy $\frac{24}{-60}>\frac{-33}{44}$
c)
$\frac{-75}{85}=\frac{-75:5}{85:5}=\frac{-15}{17}$
$\frac{34}{-68}=\frac{34:-34}{-68:-34}=\frac{-1}{2}$
Ta có:
Mẫu số chung 2 phân số: 34
$\frac{-15}{17}=\frac{-15\cdot2}{17\cdot2}=\frac{-30}{34}$
$\frac{-1}{2}=\frac{-1\cdot17}{2\cdot17}=\frac{-17}{34}$
Vì $-30<-17$ nên$\frac{-30}{34}<\frac{-17}{34}$
Vậy $\frac{-75}{85}<\frac{34}{-68}$

\(-3\left(x^2+5\right)-\left(x+1\right)\left(3x-9\right)=3x+10\)
=>\(-3x^2-15-3x^2+9x-3x+9=3x+10\)
=>\(-6x^2+6x-6-3x-10=0\)
=>\(-6x^2+3x-16=0\)
\(\text{Δ}=3^2-4\cdot\left(-6\right)\left(-16\right)=9-4\cdot96=-375< 0\)
=>Phương trình vô nghiệm
-3(x² + 5) - (x + 1)(3x - 9) = 2x + 10
-3x² - 15 - 3x² + 9x - 3x + 9 = 2x + 10
-6x² + 6x - 6 = 2x + 10
-6x² + 6x - 6 - 2x - 10 = 0
-6x² + 4x - 16 = 0
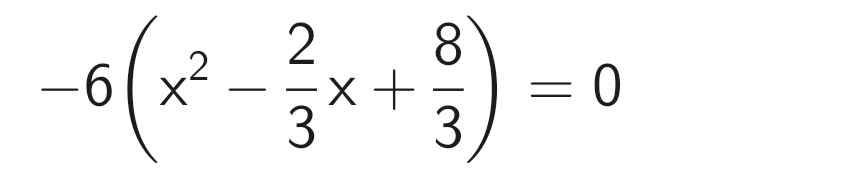 Ta có:
Ta có:
x² - 2/3 x + 8/3
= x² - 2.x.1/3 + (1/3)² + 23/9
= (x - 1/3)² + 23/9 > 0 với mọi x ∈ R
⇒ -6[(x - 1/3)² + 23/9] < 0 với mọi x ∈ R
Vậy không tìm được x thỏa mãn đề bài

a: Vì \(\widehat{xOy};\widehat{zOy}\) là hai góc kề nhau nên tia Oy nằm giữa hai tia Ox,Oz
=>\(\widehat{xOy}+\widehat{zOy}=\widehat{xOz}=120^0\)
mà \(\widehat{xOy}-\widehat{zOy}=40^0\)
nên \(\widehat{xOy}=\dfrac{120^0+40^0}{2}=80^0;\widehat{zOy}=80^0-40^0=40^0\)
b: Ta có: \(\widehat{xOm}+\widehat{xOy}=180^0\)(hai góc kề bù)
=>\(\widehat{xOm}+80^0=180^0\)
=>\(\widehat{xOm}=100^0\)
c: Ta có: \(\widehat{mOn}=\widehat{yOz}\)(hai góc đối đỉnh)
mà \(\widehat{yOz}=40^0\)
nên \(\widehat{mOn}=40^0\)
a) Ta có:
\(\widehat{xOy}+\widehat{zOy}=\widehat{xOz}=120^o\) (hai góc kề nhau)
Mà \(\widehat{xOy}-\widehat{zOy}=40^o\) nên:
\(\widehat{xOy}=\dfrac{120^o+40^o}{2}=80^o\)
Do đó: \(\widehat{zOy}=120^o-80^o=40^o\)
Vậy...
b) Ta có:
\(\widehat{xOy}+\widehat{xOm}=180^o\) (hai góc kề bù)
Mà \(\widehat{xOy}=80^o\) nên:
\(\widehat{xOm}=180^o-80^o=100^o\)
Vậy...
c) Ta có:
\(\widehat{mOn}=\widehat{zOy}\) (hai góc đối đỉnh)
Mà \(\widehat{zOy}=40^o\) nên:
\(\widehat{mOn}=40^o\)
Vậy...

a: \(\dfrac{1}{2}< \dfrac{12}{a}< \dfrac{4}{3}\)
=>\(\dfrac{12}{24}< \dfrac{12}{a}< \dfrac{12}{9}\)
=>9<a<24
mà a nguyên
nên \(a\in\left\{10;11;...;23\right\}\)
b: \(\dfrac{7}{4}< \dfrac{a}{8}< 3\)
=>\(\dfrac{14}{8}< \dfrac{a}{8}< \dfrac{24}{8}\)
=>14<a<24
mà a nguyên
nên \(a\in\left\{15;16;...;23\right\}\)
c: \(\dfrac{2}{3}< \dfrac{a-1}{6}< \dfrac{8}{9}\)
=>\(\dfrac{12}{18}< \dfrac{3\left(a-1\right)}{18}< \dfrac{16}{18}\)
=>12<3a-3<16
=>15<3a<19
=>5<a<19/3
mà a nguyên
nên a=6
d: \(\dfrac{12}{9}< \dfrac{4}{a}< \dfrac{8}{3}\)
=>\(\dfrac{8}{6}< \dfrac{8}{2a}< \dfrac{8}{3}\)
=>3<2a<6
mà a nguyên
nên 2a=4
=>a=2

\(\dfrac{1}{21}\) = \(\dfrac{1\times3}{21\times3}\) = \(\dfrac{3}{63}\) < \(\dfrac{3}{27}\)
Vậy \(\dfrac{1}{21}\) < \(\dfrac{3}{27}\)

a; \(\dfrac{4}{27}\) = \(\dfrac{4\times7}{27\times7}\) = \(\dfrac{28}{189}\)
\(\dfrac{15}{63}\) = \(\dfrac{15\times3}{63\times3}\) = \(\dfrac{45}{189}\)
\(\dfrac{28}{189}\) < \(\dfrac{45}{189}\)
- \(\dfrac{28}{189}\) > - \(\dfrac{45}{189}\)
Vậy - \(\dfrac{4}{27}\) > \(\dfrac{15}{-63}\)
b; \(\dfrac{13}{15}\) = \(\dfrac{13\times9}{15\times9}\) = \(\dfrac{117}{135}\)
\(\dfrac{9}{11}\) = \(\dfrac{9\times13}{11\times13}\) = \(\dfrac{117}{143}\)
\(\dfrac{117}{135}\) > \(\dfrac{117}{143}\)
Vậy \(\dfrac{13}{15}\) > \(\dfrac{9}{11}\)

\(\frac{x+4}{2000}+\frac{x+3}{2001}=\frac{x+2}{2002}+\frac{x+1}{2003}\\\Leftrightarrow \frac{x+4}{2000}+\frac{x+3}{2001}-\frac{x+2}{2002}-\frac{x+1}{2003}=0\\\Leftrightarrow \left(\frac{x+4}{2000}+1\right)+\left(\frac{x+3}{2001}+1\right)-\left(\frac{x+2}{2002}+1\right)-\left(\frac{x+1}{2003}+1\right)=0\\\Leftrightarrow \frac{x+2004}{2000}+\frac{x+2004}{2001}-\frac{x+2004}{2002}-\frac{x+2004}{2003}=0\\\Leftrightarrow (x+2024)\left(\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003}\right)=0\\\Leftrightarrow x+2024=0(\text{vì }\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003} \ne0)\\\Leftrightarrow x=-2024\)
Vậy phương trình có 1 nghiệm duy nhất là $x=-2024$.
 giup em bai nay em cam on
giup em bai nay em cam on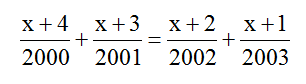
Lời giải:
Ta có:
$P(1)=(2.1-1)^6+(1-2)^7=a_7.1^7+a_6.1^6+....+a_1.1+a_0$
$\Rightarrow 1+(-1)=a_7+a_6+a_5+....+a_1+a_0$
$\Rightarrow a_7+a_6+a_5+....+a_1+a_0=0$