\(\)Gọi \(x_1,x_2\) là nghiệm của phương trình \(x^2-2\left(m-3\right)x-6m-7=0\) vs m là tham số. tính giá trị nhỏ nhất của biểu thức \(C=\left(x_1+x_2\right)^2+8x_1x_2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(AH^2=OH\cdot HM\)
=>\(OH\cdot HM=AH\cdot HB\)
b: Ta có: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)CD tại I
Xét tứ giác OHNI có \(\widehat{OHN}+\widehat{OIN}=90^0+90^0=180^0\)
nên OHNI là tứ giác nội tiếp
c: Xét tứ giác OCKI có \(\widehat{OIC}=\widehat{OKC}=90^0\)
nên OCKI là tứ giác nội tiếp

bài 3:
a: \(x^2-mx-1=0\)
\(a=1;b=-m;c=-1\)
Vì a*c=-1<0
nên phương trình luôn có hai nghiệm trái dấu
b: Theo Vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=m;x_1x_2=\dfrac{c}{a}=-1\)
\(P=\dfrac{x_1^2+x_1-1}{x_1}-\dfrac{x_2^2+x_2-1}{x_2}\)
\(=\left(x_1+1-\dfrac{1}{x_1}\right)-\left(x_2+1-\dfrac{1}{x_2}\right)\)
\(=\left(x_1-x_2\right)-\left(\dfrac{1}{x_1}-\dfrac{1}{x_2}\right)\)
\(=\left(x_1-x_2\right)-\dfrac{x_2-x_1}{x_1x_2}\)
\(=\left(x_1-x_2\right)+\dfrac{x_1-x_2}{x_1x_2}\)
\(=\left(x_1-x_2\right)+\dfrac{x_1-x_2}{-1}\)
=0

Gọi chiều rộng và chiều dài của mảnh đất lần lượt là a(m) và b(m)
(Điều kiện: a>0 và b>0)
Nếu tăng mỗi chiều của mảnh đất thêm 4m thì diện tích tăng thêm 80m2 nên ta có:
(a+4)(b+4)=ab+80
=>ab+4a+4b+16=ab+80
=>4a+4b=64
=>a+b=16(1)
Nếu giảm chiều rộng 2m và tăng chiều dài 5m thì diện tích mảnh đất không đổi nên ta có:
(a-2)(b+5)=ab
=>ab+5a-2b-10=ab
=>5a-2b=10(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=16\\5a-2b=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+2b=32\\5a-2b=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7a=42\\a+b=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=10\end{matrix}\right.\left(nhận\right)\)
Chu vi mảnh đất là \(\left(6+10\right)\cdot2=32\left(m\right)\)
Đặt: Độ dài chiều dài và rộng của mảnh vườn lần lượt là a và b (m; a>b>0)
=> Diện tích mảnh đất đó là ab (m2)
+) Nếu tăng mỗi chiều của mảnh đất đó thêm 4m thì diện tích mảnh đất đó tăng thêm 80m2
=> (a+4)(b+4)=ab+80 (m2)
=> ab+4a+4b+16=ab+80
=>4a+4b+16=80
=>4a+4b=64
=> 4(a+b)=64
=> a+b=16 (1)
+)Nếu giảm chiều rộng 2m và tăng chiều dài thêm 5m thì diện tích mảnh vườn không đổi
=> (a+5)(b-2)=ab(m2)
=>ab-2a+5b-10=ab
=>-2a+5b=10 (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=16\Rightarrow2\left(a+b\right)=2a+2b=32\\-2a+5b=10\end{matrix}\right.\)
\(2a+2b-2a+5b=7b=42\)
\(b=6\)
Thay b = 6 vào (1)
=> a + 6 = 16
=> a = 10
Có a>b>0 (do 10>6>0)
=> tmđk: a = 10 và b = 6
=> Độ dài của chiều dài và rộng lần lượt là 10m và 6m
=> Chu vi mảnh vườn đó là: (10+6).2=32(m)
Đ/S: 32m

Xét ΔIMB vuông tại M và ΔINC vuông tại N có
\(\widehat{MIB}=\widehat{NIC}\)(hai góc đối đỉnh)
Do đó: ΔIMB~ΔINC
=>\(\dfrac{IM}{IN}=\dfrac{IB}{IC}\)
=>\(IM\cdot IC=IB\cdot IN\)

Gọi vận tốc lúc đầu của người đó là x(km/h)
(Điều kiện: x>0)
Thời gian dự kiến ban đầu là \(\dfrac{90}{x}\left(giờ\right)\)
1h9p=1,15h
Sau 1,15h, người đó đi được 1*x=x(km)
Độ dài quãng đường còn lại là 90-x(km)
Thời gian thực tế đi hết quãng đường là:
\(1,15+\dfrac{90-x}{x+4}\left(giờ\right)\)
Theo đề, ta có:
\(\dfrac{90}{x}=1,15+\dfrac{90-x}{x+4}\)
=>\(\dfrac{90}{x}-\dfrac{90-x}{x+4}=1,15\)
=>\(\dfrac{90x+360-90x+x^2}{x\left(x+4\right)}=1,15\)
=>\(1,15\left(x^2+4x\right)=x^2+360\)
=>\(1,15x^2+4,6x-x^2-360=0\)
=>\(0,15x^2+4,6x-360=0\)
=>\(\left[{}\begin{matrix}x=36\left(nhận\right)\\x=-\dfrac{200}{3}\left(loại\right)\end{matrix}\right.\)
Vậy: Vận tốc lúc đầu của người đó là 36km/h

a.
Do MC, MD là các tiếp tuyến \(\Rightarrow\widehat{DMO}=\widehat{DNO}=90^0\)
\(\Rightarrow\)M và N cùng nhìn OD dưới 1 góc vuông nên DMON nội tiếp
b.
Xét hai tam giác MIA và NIM có:
\(\left\{{}\begin{matrix}\widehat{MIA}-chung\\\widehat{IMA}=\widehat{INM}\left(\text{cùng chắn MA}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MIA\sim\Delta NIM\left(g.g\right)\)
\(\Rightarrow\dfrac{MI}{IN}=\dfrac{IA}{MI}\Rightarrow MI^2=IA.IN\)
c.
Theo t/c hai tiếp tuyến cắt nhau ta có \(DM=DN\)
Lại có \(OM=ON=R\)
\(\Rightarrow OD\) là trung trực MN
\(\Rightarrow OD\) vuông góc MN tại H
Xét hai tam giác OHM và OMD có:
\(\left\{{}\begin{matrix}\widehat{MOH}-chung\\\widehat{OHM}=\widehat{OMD}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta OHM\sim\Delta OMD\left(g.g\right)\)
\(\Rightarrow\dfrac{OH}{OM}=\dfrac{OM}{OD}\Rightarrow OM^2=OH.OD\)
\(\Rightarrow R^2=OH.\left(OH+HD\right)=3.\left(3+5\right)=24\)
\(\Rightarrow R=2\sqrt{6}\)

Lời giải:
Ta có:
$\sin B = \frac{AH}{AB}\Rightarrow AB=\frac{AH}{\sin B}=\frac{3}{\frac{3}{4}}=4$
$\sin B=\frac{3}{4}\Rightarrow \widehat{B}=48,6^0$
$\widehat{C}=90^0-\widehat{B}=90^0-48,6^0=41,4^0$


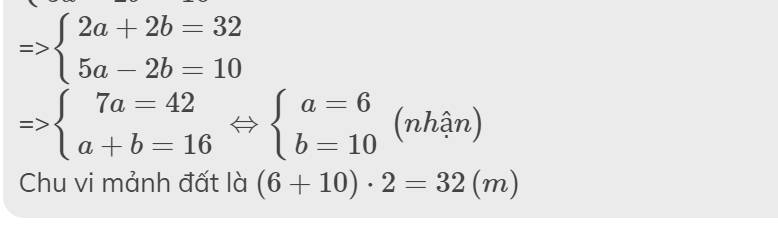

\(\text{Δ}=\left[-2\left(m-3\right)\right]^2-4\cdot1\cdot\left(-6m-7\right)\)
\(=4\left(m^2-6m+9\right)+4\left(6m+7\right)\)
\(=4m^2-24m+36+24m+28\)
\(=4m^2+64>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=2\left(m-3\right);x_1x_2=\dfrac{c}{a}=-6m-7\)
\(C=\left(x_1+x_2\right)^2+8x_1x_2\)
\(=\left(2m-6\right)^2+8\left(-6m-7\right)\)
\(=4m^2-24m+36-48m-56\)
\(=4m^2-72m-20\)
\(=4\left(m^2-18m-5\right)\)
\(=4\left(m^2-18m+81-86\right)\)
\(=4\left(m-9\right)^2-344>=-344\forall m\)
Dấu '=' xảy ra khi m=9