Bài 2: Cho △ABC vuông tại A, đường phân giác BE . Kẻ EH vuông góc với BC (H thuộc BC ). Gọi K là giao điểm của AB và HE. Chứng minh rằng
a,△ABE = △HBE
b,BE là đường trung trục của đoạn thẳng AH
c,EK=EC và AE≤EC
có vẽ hình thì càng tốt :)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

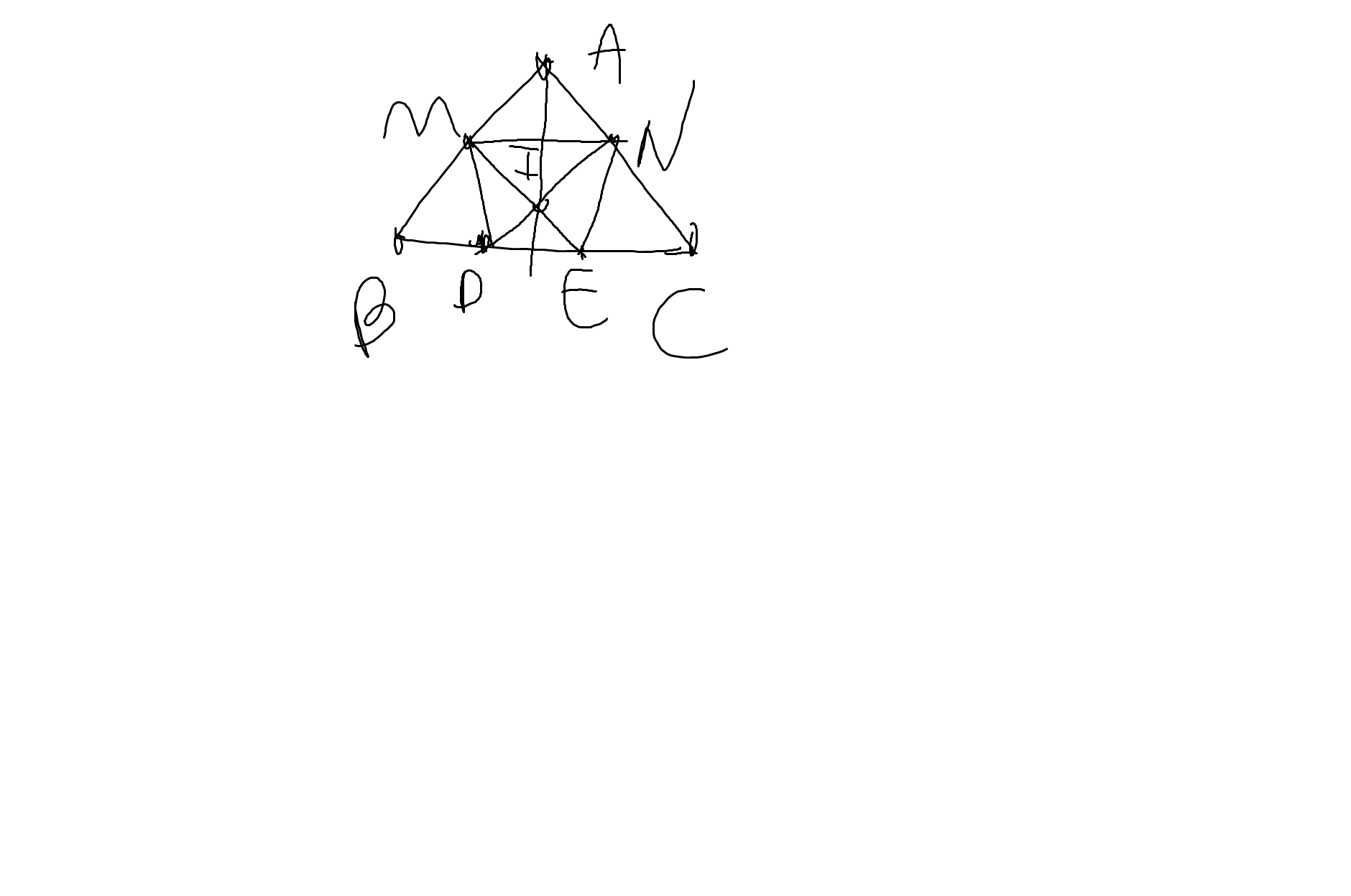
a: BE=BD+DE
CD=CE+DE
mà BD=CE
nên BE=CD
Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔMBE và ΔNCD có
MB=NC
\(\widehat{MBE}=\widehat{NCD}\)
BE=CD
Do đó: ΔMBE=ΔNCD
=>ME=ND
b:
Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
=>MN//DE
Xét tứ giác MNED có
MN//ED
ME=ND
Do đó: MNED là hình bình hành
=>MD=NE
Xét ΔMDE và ΔNED có
MD=NE
DE chung
ME=ND
Do đó: ΔMDE=ΔNED
=>\(\widehat{MED}=\widehat{NDE}\)
=>\(\widehat{IDE}=\widehat{IED}\)
=>ΔIED cân tại I
c: Ta có: \(\widehat{IDE}+\widehat{IDB}=180^0\)(hai góc kề bù)
\(\widehat{IED}+\widehat{IEC}=180^0\)(hai góc kề bù)
mà \(\widehat{IDE}=\widehat{IED}\)
nên \(\widehat{IDB}=\widehat{IEC}\)
Xét ΔIDB và ΔIEC có
ID=IE
\(\widehat{IDB}=\widehat{IEC}\)
DB=EC
Do đó: ΔIDB=ΔIEC
=>IB=IC
=>I nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AI là đường trung trực của BC
=>AI\(\perp\)BC

Bài 7:
p là số nguyên tố lớn hơn 3
=>p=3k+1 hoặc p=3k+2
Nếu p=3k+1 thì \(8p+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)⋮3\)
=>Loại
=>p=3k+2
\(4p+1=4\left(3k+2\right)+1=12k+9=3\left(4k+3\right)⋮3\)
=>4p+1 là hợp số
Bài 6:
a: TH1: p=3
p+2=3+2=5; p+4=3+4=7
=>Nhận
TH2: p=3k+1
p+2=3k+1+2=3k+3=3(k+1)
=>Loại
TH3: p=3k+2
p+4=3k+2+4=3k+6=3(k+2)
=>Loại
b: TH1: p=5
p+2=5+2=7; p+6=5+6=11; p+18=5+18=23; p+24=5+24=29
=>Nhận
TH2: p=5k+1
p+24=5k+1+24=5k+25=5(k+5)
=>Loại
TH3: p=5k+2
p+18=5k+2+18=5k+20=5(k+4)
=>Loại
TH4: p=5k+3
p+2=5k+3+2=5k+5=5(k+1)
=>Loại
TH5: p=5k+4
p+6=5k+4+6=5k+10=5(k+2)
=>Loại
Vậy: p=5
Bài 5:
Với p=2 => 7p+5=7*2 + 5 = 19 (tm)
Với p>3
TH1: p=3k+1
=> 7(3k+1)+5=21k+7+5=21k+12=3(7k+4) ⋮ 3
=> 7p+5 là hợp số
TH2: p=3k+2
=>7(3k+2)+5=21k+14+5=21k+19
Vì p là số nguyên tố lớn hơn 3 => p lẻ => 3k + 2 lẻ => 3k lẻ => k lẻ
k lẻ => 21k lẻ => 21k + 19 chẵn => 21k+19 ⋮ 2
=> 7p+5 là hơn số
Vậy có p=2 là thỏa mãn

Diện tích xung quanh của căn nhà là:
\(2\times\left(25+6\right)\times5=310\left(m^2\right)\)
Diện tích trần nhà là:
\(25\times6=150\left(m^2\right)\)
Diện tích cửa ra vào là:
\(3\times15=45\left(m^2\right)\)
Diện tích hai cửa sổ là:
\(2\times\left(1\times1\right)=2\left(m^2\right)\)
Diện tích cần sơn là:
\(\left(310+150\right)-\left(45+2\right)=413\left(m^2\right)\)
Chi phí để sơn căn phòng là:
\(413:1,2\times30000=10325000\)
Vậy...

a: Ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\)(hai góc kề bù)
=>\(\widehat{yOz}+120^0=180^0\)
=>\(\widehat{yOz}=60^0\)
b: Om là phân giác của góc xOy
=>\(\widehat{xOm}=\widehat{yOm}=\dfrac{\widehat{xOy}}{2}=60^0\)
Ta có: \(\widehat{xOm}+\widehat{zOm}=180^0\)(hai góc kề bù)
=>\(\widehat{zOm}+60^0=180^0\)
=>\(\widehat{zOm}=120^0\)
c: Ta có: \(\widehat{yOz}=\widehat{yOm}\left(=60^0\right)\)
mà tia Oy nằm giữa hai tia Oz và Om(Vì \(\widehat{yOz}+\widehat{yOm}=\widehat{zOm}\))
nên Oy là phân giác của góc zOm

Ta có: \(\widehat{AOD}=\widehat{BOC}\)(hai góc đối đỉnh)
mà \(\widehat{AOD}+\widehat{BOC}=110^0\)
nên \(\widehat{AOD}=\widehat{BOC}=\dfrac{110^0}{2}=55^0\)
Ta có: \(\widehat{AOD}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(\widehat{AOC}+55^0=180^0\)
=>\(\widehat{AOC}=125^0\)
Ta có: \(\widehat{AOC}=\widehat{BOD}\)(hai góc đối đỉnh)
mà \(\widehat{AOC}=125^0\)
nên \(\widehat{BOD}=125^0\)

Ta có: \(\widehat{BOC}=\widehat{AOD}\)(hai góc đối đỉnh)
mà \(\widehat{BOC}=45^0\)
nên \(\widehat{AOD}=45^0\)
Ta có: \(\widehat{AOD}+\widehat{DOB}=180^0\)(hai góc kề bù)
=>\(\widehat{DOB}+45^0=180^0\)
=>\(\widehat{DOB}=135^0\)
Ta có: \(\widehat{DOB}=\widehat{AOC}\)(hai góc đối đỉnh)
mà \(\widehat{DOB}=135^0\)
nên \(\widehat{AOC}=135^0\)

b: (2x+1):2=12:3
=>(2x+1):2=4
=>2x+1=2*4=8
=>2x=7
=>\(x=\dfrac{7}{2}\)
d: \(\dfrac{2x-14}{3}=\dfrac{12}{9}\)
=>\(\dfrac{2x-14}{3}=\dfrac{4}{3}\)
=>2x-14=4
=>2x=18
=>x=9

a: tia OB nằm giữa hai tia OA và OC
=>\(\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\)
=>\(\widehat{BOC}=165^0-20^0=145^0\)
b: Ta có: \(\widehat{BOC}+\widehat{COD}=180^0\)(hai góc kề bù)
=>\(\widehat{COD}+145^0=180^0\)
=>\(\widehat{COD}=35^0\)

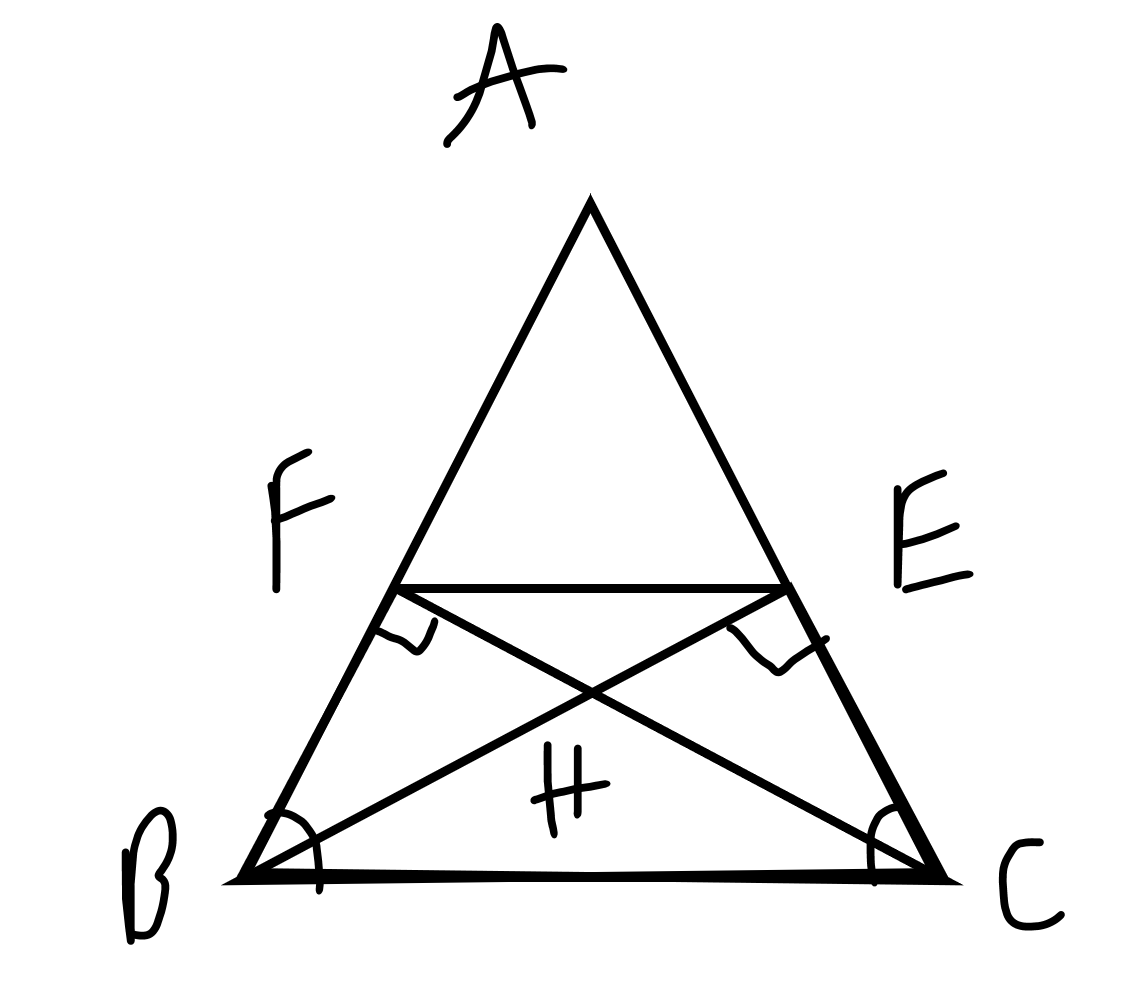
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔAEB=ΔAFC
=>BE=CF
b: ΔAEB=ΔAFC
=>AE=AF
Xét ΔAFH vuông tại F và ΔAEH vuông tại E có
AH chung
AF=AE
Do đó: ΔAFH=ΔAEH
=>HE=HF
=>ΔHEF cân tại H
c: Xét ΔABC có \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
nên EF//BC
d: Ta có: AE=AF
=>A nằm trên đường trung trực của EF(1)
Ta có: HE=HF
=>H nằm trên đường trung trực của EF(2)
Từ (1),(2) suy ra AH là đường trung trực của EF
=>AH\(\perp\)EF


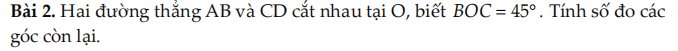

a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>BA=BH và EA=EH
Ta có: BA=BH
=>B nằm trên đường trung trực của AH(1)
Ta có: EA=EH
=>E nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra BE là đường trung trực của AH
c: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔEAK=ΔEHC
=>EK=EC
mà EK>EA(ΔEAK vuông tại A)
nên EC>EA