Tính diện tích hình bên biết ABCD hình thang là AB bằng 6 cm CD = 12 cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔABE~ΔACF
b: Sửa đề: Qua B kẻ song song với CF
Xét tứ giác BICK có
BI//CK
BK//CI
Do đó: BICK là hình bình hành
BI//CK
BI\(\perp\)AC
Do đó: CK\(\perp\)CA
CI//BK
CI\(\perp\)AB
Do đó:BK\(\perp\)BA
Xét tứ giác ABKC có \(\widehat{ABK}+\widehat{ACK}=90^0+90^0=180^0\)
nên ABKC là tứ giác nội tiếp đường tròn đường kính tâm M, đường kính AK
Xét (M) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AKC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AKC}\)
Xét ΔAFI vuông tại F và ΔACK vuông tại C có
\(\widehat{FIA}=\widehat{AKC}\left(=\widehat{ABC}\right)\)
Do đó: ΔAFI~ΔACK
=>\(\dfrac{FA}{CA}=\dfrac{FI}{CK}\)
=>\(\dfrac{FI}{FA}=\dfrac{CK}{CA}\)

Sửa đề: \(\dfrac{x}{2}=\dfrac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x-2y}{2-2\cdot3}=\dfrac{8}{-4}=-2\)
=>\(x=-2\cdot2=-4;y=-2\cdot3=-6\)
\(A=x^3+y^2=\left(-4\right)^3+\left(-6\right)^2=-64+36=-28\)

c: \(P=A:B=\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}:\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
\(=\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{\sqrt{x}-1}=\dfrac{2\sqrt{x}+3}{\sqrt{x}-1}\)
Để P là số nguyên thì \(2\sqrt{x}+3⋮\sqrt{x}-1\)
=>\(2\sqrt{x}-2+5⋮\sqrt{x}-1\)
=>\(5⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{2;0;6;-4\right\}\)
=>\(\sqrt{x}\in\left\{2;0;6\right\}\)
=>\(x\in\left\{4;0;36\right\}\)
mà x lớn nhất
nên x=36

Cửa hàng đã bán được:
\(\dfrac{3}{8}+\dfrac{2}{7}=\dfrac{21}{56}+\dfrac{16}{56}=\dfrac{37}{56}\)(tổng số gạo)

Số học sinh khá chiếm:
\(\dfrac{1}{5}:\dfrac{3}{7}=\dfrac{1}{5}\times\dfrac{7}{3}=\dfrac{7}{15}\)(tổng số học sinh)
Số học sinh trung bình chiếm:
\(1-\dfrac{1}{5}-\dfrac{7}{15}=\dfrac{4}{5}-\dfrac{7}{15}=\dfrac{5}{15}=\dfrac{1}{3}\)(tổng số học sinh)
Tổng số học sinh là \(45:\dfrac{1}{3}=135\left(bạn\right)\)
Số học sinh giỏi là \(135\cdot\dfrac{1}{5}=27\left(bạn\right)\)
Số học sinh khá là:
135-45-27=63(bạn)

a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
=>\(\widehat{ACB}=50^0\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=180^0-2\cdot50^0=80^0\)
b: Xét ΔNBC vuông tại N và ΔMCB vuông tại M có
BC chung
\(\widehat{NBC}=\widehat{MCB}\)(ΔABC cân tại A)
Do đó: ΔNBC=ΔMCB
=>CN=MB
c: ΔNBC=ΔMCB
=>\(\widehat{NCB}=\widehat{MBC}\)
=>\(\widehat{HBC}=\widehat{HCB}\)
=>ΔHBC cân tại H
Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
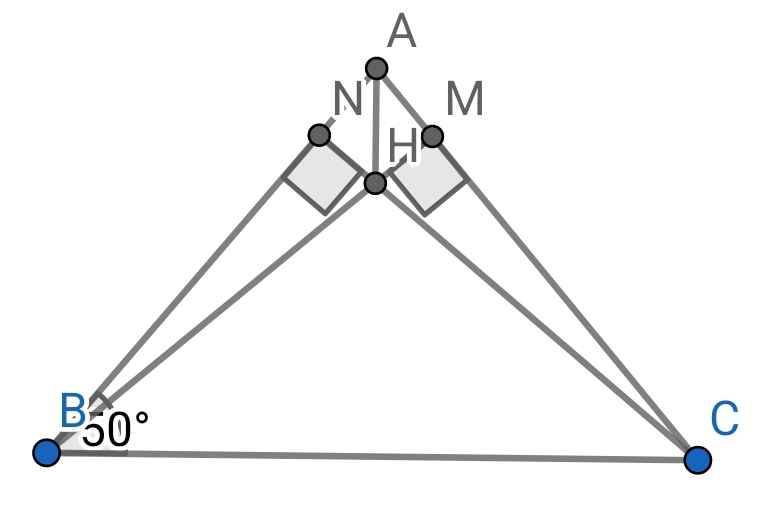
a) ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = 50⁰
∠ABC + ∠ACB + ∠BAC = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠BAC = 180⁰ - (∠ABC + ∠ACB)
= 180⁰ - (50⁰ + 50⁰)
= 80⁰
b) Ta có:
∠ABC = ∠ACB (cmt)
⇒ ∠NBC = ∠MCB
Xét hai tam giác vuông: ∆NBC và ∆MCB có:
BC là cạnh chung
∠NBC = ∠MCB (cmt)
⇒ ∆NBC = ∆MCB (cạnh huyền - góc nhọn)
⇒ CN = BM (hai cạnh tương ứng)
Hay BM = CN
c) ∆ABC cân tại A (gt)
BM là đường cao (gt)
CN là đường cao thứ hai (gt)
⇒ AH là đường cao thứ ba
⇒ AH cũng là đường phân giác
⇒ AH là tia phân giác của ∠BAC
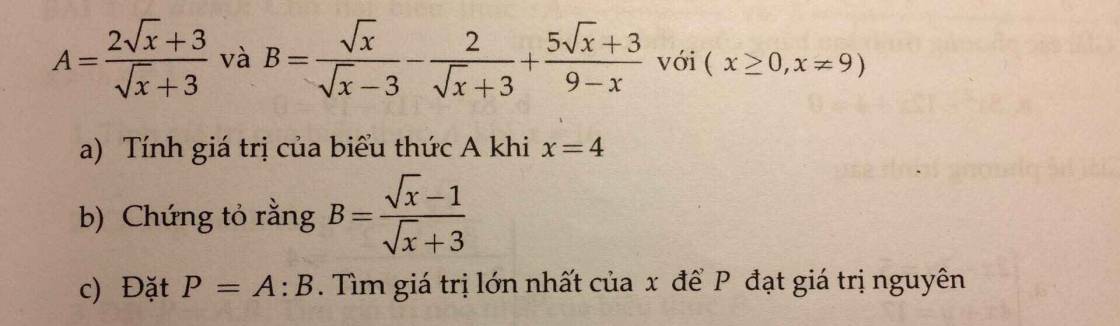
6+12=18