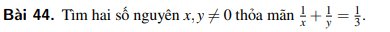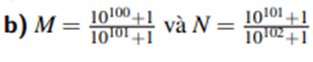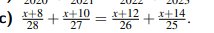Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để giải quyết bài toán này, chúng ta cần xem xét cách ánh sáng phản xạ qua gương phẳng khi gương quay.
Trường hợp a: Trục quay O đi qua điểm tới I
-
Phân tích tình huống:
- Giả sử gương phẳng M đang ở một góc với tia tới, và ánh sáng phản xạ theo định luật phản xạ (góc tới = góc phản xạ).
- Khi gương quay quanh điểm tới I, mỗi điểm trên gương quay cùng một góc α (alpha) quanh điểm I.
-
Tính toán góc quay của tia phản xạ:
-
Khi gương quay một góc α quanh điểm I, các góc tới và phản xạ thay đổi cùng với góc quay của gương.
-
Góc giữa tia tới và gương lúc đầu là góc tới (θ). Khi gương quay một góc α quanh điểm tới I, góc giữa tia tới và gương vẫn là θ (vì điểm tới không thay đổi).
-
Tia phản xạ cũng quay quanh điểm I một góc α.
-
Do định luật phản xạ (góc tới = góc phản xạ), và gương quay góc α quanh điểm tới, tia phản xạ sẽ quay một góc 2α so với vị trí ban đầu.
Kết luận: Trong trường hợp này, khi gương quay quanh điểm tới I một góc α, tia phản xạ quay một góc 2α.
-
Trường hợp b: Trục quay O ở ngoài điểm tới I
-
Phân tích tình huống:
- Giả sử trục quay O nằm ngoài điểm tới I, nghĩa là gương quay quanh một trục không đi qua điểm tới.
-
Tính toán góc quay của tia phản xạ:
-
Trong trường hợp này, khi gương quay một góc α quanh trục O, điểm tới I di chuyển cùng với gương, và góc tới có thể thay đổi.
-
Góc giữa tia tới và gương ban đầu là θ. Khi gương quay một góc α quanh trục O, góc giữa gương và tia phản xạ thay đổi, làm cho tia phản xạ quay một góc không thể tính trực tiếp từ α một cách đơn giản.
-
Để xác định góc quay chính xác của tia phản xạ, chúng ta cần áp dụng các phép toán phức tạp hơn về hình học và động học của ánh sáng trong không gian 3D.
Kết luận: Trong trường hợp này, góc quay của tia phản xạ không đơn giản là 2α mà phụ thuộc vào cách gương quay và cấu trúc không gian. Tuy nhiên, trong thực tiễn, thường sử dụng các phần mềm hoặc tính toán chi tiết hơn để xác định chính xác.
-
Tóm lại, trong trường hợp gương quay quanh điểm tới I, tia phản xạ quay một góc 2α. Trong trường hợp gương quay quanh một trục ngoài điểm tới I, góc quay của tia phản xạ cần được tính toán cụ thể hơn dựa trên vị trí trục quay và cách ánh sáng phản xạ.

Gọi nửa quãng đường là S
\(t_1\) là thời gian đi hết nửa quãng đường đầu
\(t_1=\dfrac{s}{12}\)
\(t_2\) là thời gian đi hết nửa quãng đường sau
\(t_2=\dfrac{S}{v_2}\)
\(v_{tb}=\dfrac{S+S}{t_1+t_2}=\dfrac{2S}{\dfrac{S}{12}+\dfrac{S}{v_2}}=8\)
\(\Leftrightarrow\dfrac{2S}{\dfrac{S\left(12+v_2\right)}{12v_2}}=8\Leftrightarrow\dfrac{24v_2}{12+v_2}=8\Rightarrow v_2=6\) km/h

Câu 1: D
→ A, B, C đều đọc ở phần gạch chân là: /æ/
⇌ Riêng câu D đọc là: /ˈfestɪvl/ Không có /æ/ nên suy ra nó có phát âm khác so với những từ còn lại.
Câu 2: Câu này đề cho sai cậu nhé, phần gạch chân có phát âm là âm /eɪ/ giống nhau nên không có từ nào phát âm khác cả.
Câu 3: Các ed của câu này đều phát âm là /id/ nên suy ra không có câu trả lời đúng
1 sai đề
2 C (đọc là e còn lại là ei)
3 A (đọc là id còn lại là t)

\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{3}\)
\(\dfrac{x+y}{xy}=\dfrac{1}{3}\)
\(3\left(x+y\right)=xy\)
\(xy-3x-3y=0\)
\(xy-3x-3y+9=9\)
\(x\left(y-3\right)-3\left(y-3\right)=9\)
\(\left(x-3\right)\left(y-3\right)=9\)
Ta có bảng sau:
| x-3 | -9 | -3 | -1 | 1 | 3 | 9 |
| y-3 | -1 | -3 | -9 | 9 | 3 | 1 |
| x | -6 | 0 (loại) | 2 | 4 | 6 | 12 |
| y | 2 | 0 (loại) | -6 | 12 | 6 | 4 |
Vậy \(\left(x;y\right)=\left(-6;2\right);\left(2;-6\right);\left(4;12\right);\left(6;6\right);\left(12;4\right)\)

\(10M=\dfrac{10.\left(10^{100}+1\right)}{10^{101}+1}=\dfrac{10^{101}+10}{10^{101}+1}=\dfrac{10^{101}+1+9}{10^{101}+1}=1+\dfrac{9}{10^{101}+1}\)
\(10N=\dfrac{10.\left(10^{101}+1\right)}{10^{102}+1}=\dfrac{10^{102}+10}{10^{102}+1}=\dfrac{10^{102}+1+9}{10^{102}+1}=1+\dfrac{9}{10^{102}+1}\)
Do \(10^{101}< 10^{102}\Rightarrow10^{101}+1< 10^{102}+1\)
\(\Rightarrow\dfrac{9}{10^{101}+1}>\dfrac{9}{10^{102}+1}\)
\(\Rightarrow1+\dfrac{9}{10^{101}+1}>1+\dfrac{9}{10^{102}+1}\)
\(\Rightarrow10M>10N\)
\(\Rightarrow M>N\)

\(\dfrac{x+8}{28}+\dfrac{x+10}{27}=\dfrac{x+12}{26}+\dfrac{x+14}{25}\)
\(\left(\dfrac{x+8}{28}+2\right)+\left(\dfrac{x+10}{27}+2\right)=\left(\dfrac{x+12}{26}+2\right)+\left(\dfrac{x+14}{25}+2\right)\)
\(\dfrac{x+64}{28}+\dfrac{x+64}{27}=\dfrac{x+64}{26}+\dfrac{x+64}{25}\)
\(\dfrac{x+64}{28}+\dfrac{x+64}{27}-\dfrac{x+64}{26}-\dfrac{x+64}{25}=0\)
\(\left(x+64\right)\left(\dfrac{1}{28}+\dfrac{1}{27}-\dfrac{1}{26}-\dfrac{1}{25}\right)=0\)
\(x+64=0\) (do \(\dfrac{1}{28}+\dfrac{1}{27}-\dfrac{1}{26}-\dfrac{1}{25}\ne0\))
\(x=-64\)

a: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(30^0< 100^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
=>\(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
=>\(\widehat{yOz}=100^0-30^0=70^0\)
Vì tia Ot nằm trong góc yOz
nên tia Ot nằm giữa hai tia Oy,Oz
=>\(\widehat{yOt}+\widehat{zOt}=\widehat{yOz}\)
=>\(\widehat{zOt}=70^0-20^0=50^0\)
Vì \(\widehat{yOt}< \widehat{zOt}\left(20^0< 50^0\right)\)
nên Ot không là phân giác của góc yOz
b: Vì \(\widehat{zOt}< \widehat{zOx}\left(50^0< 100^0\right)\)
nên tia Ot nằm giữa hai tia Oz và Ox
=>\(\widehat{tOz}+\widehat{tOx}=\widehat{xOz}\)
=>\(\widehat{xOt}=100^0-50^0=50^0\)
Ta có: tia Ot nằm giữa hai tia Ox và Oz
mà \(\widehat{xOt}=\widehat{zOt}\left(=50^0\right)\)
nên Ot là phân giác của góc xOz

a) Căn bậc 2 số học của `121` là `11`
Căn bậc 2 của `121` là ` +-11`
b) Căn bậc 2 số học của `(-5/6)^2 ` là ` 5/6`
Căn bậc 2 của `(-5/6)^2` là ` +-5/6`