SO SÁNH : A = 3^123 +1 / 3^125 + 1 và B = 3^122/ 3^124 + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


7x - 33 = 27 : 24
7\(x\) - 27 = 23
7\(x\) = 8 + 27
7\(x\) = 35
\(x\) = 5

\(3n+9⋮n+1\left(n\inℕ\right)\)
\(\Rightarrow3n+9-3\left(n+1\right)⋮n+1\)
\(\Rightarrow3n+9-3n-3⋮n+1\)
\(\Rightarrow6⋮n+1\)
\(\Rightarrow n+1\in\left\{1;2;3;6\right\}\)
\(\Rightarrow n\in\left\{0;1;2;5\right\}\left(n\inℕ\right)\)

Bổ sung đề : Tìm n thuộc Z
+) \(11⋮\left(n-2\right)=>n-2\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\\ =>n\in\left\{3;1;13;-9\right\}\)
+) \(\left(n+7\right)⋮\left(n-3\right)\\ =>\left(n-3\right)+10⋮\left(n-3\right)\\ =>10⋮\left(n-3\right)\\ =>n-3\inƯ\left(10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\\ =>n\in\left\{4;2;5;1;8;-2;13;-7\right\}\)

A = 5 + 52 + 53 +...+ 58
A = (5 + 52) +( 53 + 54) +...+ ( 57 + 58)
A = 30 + 52.(5 + 52) +...+ 56.(5 + 52)
A = 30.( 1 + 52 +...+ 56) (đpcm)

Bài 2
a) x/8 = 5,4/3
x = 8 . 5,4/3
x = 14,4
b) 2,5 : 7,5 = x : 3/5
x = 3/5 × 1/3
x = 1/5
c) 2 2/3 : x = 1 7/9 : 0,2
8/3 : x = 16/9 : 1/5
x = 8/3 : (16/9 : 1/5)
x = 8/3 : 80/9
x = 3/10
d) 4/x = x/0,16
x² = 4 . 0,16
x² = 0,64
x = 0,8 hoặc x = -0,8
Bài 3
a) x/9 = y/11 và x + y = 60
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/9 + y/11 = (x + y)/(9 + 11) = 60/20 = 3
x/9 = 3 ⇒ x = 9.3 = 27
y/11 = 3 ⇒ y = 11.3 = 33
Vậy x = 27; y = 33
b) x/3 = y/5 ⇒ 2x/6 = y/5 và 2x - y = 8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x/6 = y/5 = (2x - y)/(6 - 5) = 8/1 = 8
2x/6 = 8 ⇒ x = 6.8:2 = 24
y/5 = 8 ⇒ y = 5.8 = 40
Vậy x = 24; y = 40
c) 7x = 4y ⇒ y/7 = x/4 và y - x = 24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
y/7 = x/4 = (y - x)/(7 - 4) = 24/3 = 8
x/4 = 8 ⇒ x = 4.8 = 32
y/7 = 8 ⇒ y = 7.8 = 56
Vậy x = 32; y = 56

A = 2.4.6.8.10.12 - 40
A = 40.2.6.8.12 - 40
A =40.( 2.6.8.12 - 1) ⋮ 20; 8
A = 2.4.6.8.10.12 - 40
2.4.6.8.10.12 ⋮ 6
40 không chia hết cho 6
Vậy A không chia hết cho 6
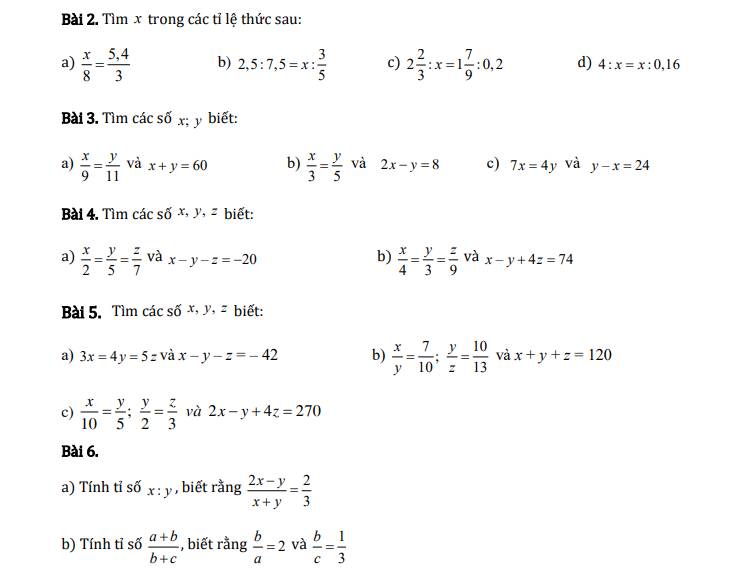
A = \(\dfrac{3^{123}+1}{3^{125}+1}\) Vì 3123 + 1 < 2125 + 1 Nên A = \(\dfrac{3^{123}+1}{3^{125}+1}\)< \(\dfrac{3^{123}+1+2}{3^{125}+1+2}\)
A < \(\dfrac{3^{123}+3}{3^{125}+3}\) = \(\dfrac{3.\left(3^{122}+1\right)}{3.\left(3^{124}+1\right)}\) = \(\dfrac{3^{122}+1}{3^{124}+1}\) = B
Vậy A < B