
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều dài ban đầu của hình chữ nhật đó là x(m) (đk : 0 < x < 32)
Khi đó chiều rộng ban đầu của hình chữ nhật đó là : 32 - x (m)
Diện tích ban đầu của hình chữ nhật đó là : x(32 - x) (m²)
Chiều dài của hình chữ nhật đó sau khi bị giảm 2m là : x - 2 (m)
Chiều rộng của hình chữ nhật đó sau khi tăng 3m là : 32 - x +3 = 35 - x (m)
Diện tích của hình chữ nhật đó sau khi tăng chiều rộng lên 3m và giảm chiều dài 2m là : (x - 2)(35 - x) (m²)
Theo đề bài , ta có phương trình : (x - 2)(35 - x) - x(32 - x) = 20
35x - x² - 70 + 2x - 32x + x² = 20
5x - 70 = 20
5x = 90
x = 18
Giá trị này của x thỏa mã điều kiện của ẩn
Diện tích hình chữ nhật ban đầu là : 18(32 - 18) = 252 (m²)
Vậy diện tích hình chữ nhật ban đầu là 252 m²



a: x-4=1
=>x=5
Thay x=5 vào B, ta được:
\(B=\dfrac{5+1}{5-3}=\dfrac{6}{2}=3\)
b: \(A=\dfrac{x}{x-3}-\dfrac{x+1}{x+3}+\dfrac{3x-3}{x-3}\)
\(=\dfrac{x+3x-3}{x-3}-\dfrac{x+1}{x+3}\)
\(=\dfrac{4x-3}{x-3}-\dfrac{x+1}{x+3}\)
\(=\dfrac{\left(4x-3\right)\left(x+3\right)-\left(x-3\right)\left(x+1\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{4x^2+12x-3x-9-\left(x^2-2x-3\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{4x^2+9x-9-x^2+2x+3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{3x^2+11x-6}{\left(x-3\right)\left(x+3\right)}\)
c: \(M=B:A=\dfrac{3x^2+11x-6}{\left(x-3\right)\left(x+3\right)}:\dfrac{x}{x-3}\)
\(=\dfrac{3x^2+11x-6}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{x}=\dfrac{3x^2+11x-6}{x^2+3x}\)
M=5
=>\(5\left(x^2+3x\right)=3x^2+11x-6\)
=>\(5x^2+15x-3x^2-11x+6=0\)
=>\(2x^2-4x+6=0\)
=>\(x^2-2x+3=0\)
=>\(\left(x-1\right)^2+2=0\)(vô lý)

Gọi vận tốc của xe máy là x(km/h)
(ĐK: x>0)
Vận tốc của ô tô là x+10(km/h)
Tổng vận tốc của hai xe là 140:2=70(km/h)
Do đó,ta có phương trình:
x+x+10=70
=>2x=60
=>x=30(nhận)
vậy: vận tốc xe máy là 30km/h
vận tốc ô tô là 30+10=40km/h

3 - 4x(25 - 2x) = 8x² + x - 300
3 - 100x + 8x² = 8x² + x - 300
-100x + 8x² - 8x² - x = -300 - 3
-101x = -303
x = -303 : (-101)
x = 3
Vậy S = {3}

ĐKXĐ: \(x\notin\left\{0;3;-3;-\dfrac{3}{2}\right\}\)
\(\dfrac{x^2-6}{x-3}+\dfrac{x^2+3x}{2x+3}\left(\dfrac{x}{x^2-9}-\dfrac{x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\left(\dfrac{x}{\left(x-3\right)\left(x+3\right)}-\dfrac{x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\dfrac{x^2-\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x^2-x^2-6x-9}{\left(2x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-6}{x-3}-\dfrac{3}{x-3}=\dfrac{x^2-9}{x-3}=x+3\)

Đây là dạng toán nâng cao chuyên đề phép chia đa thức, cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay, Olm.vn sẽ hưỡng dẫn các em giải chi tiết dạng này bằng bezout như sau:
Giải:
F(\(x\)) = \(x^3\) + a\(x\) + b ⋮ (\(x\) + 1)(\(x\) + 2)
Theo bezout ta có: F(\(x\)) ⋮ (\(x\) + 1)(\(x\) + 2) khi và chỉ khi: \(\left\{{}\begin{matrix}F\left(-1\right)=0\\F\left(-2\right)=0\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}F\left(-1\right)=\left(-1\right)^3+a.\left(-1\right)+b=0\\F\left(-2\right)=\left(-2\right)^3+a.\left(-2\right)+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}-1-a+b=0\\-8-2a+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}-1-a+b-\left(-8-2a+b\right)=0\\-8-2a+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}-1-a+b+8+2a-b=0\\-8-2a+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\left(-1+8\right)+\left(2a-a\right)+\left(b-b\right)=0\\-8-2a+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}7+a=0\\-8-2a+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a=-7\\-8-2a+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a=-7\\-8-2.\left(-7\right)+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a=-7\\6+b=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a=-7\\b=-6\end{matrix}\right.\)
Kết luận: \(x^3\) + a\(x\) + b ⋮ (\(x\) + 1)(\(x\) + 2) ⇔ a = -7; b = - 6
Vậy \(x^3\) + a\(x\) + b = \(x^3\) - 7\(x\) - 6

a: Xét ΔCNI vuông tại N và ΔCAB vuông tại A có
\(\widehat{NCI}\) chung
Do đó: ΔCNI~ΔCAB
=>\(\dfrac{CN}{CA}=\dfrac{CI}{CB}\)
=>\(CN\cdot CB=CI\cdot CA\)
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
\(NB^2-NC^2\)
\(=BI^2-IN^2-\left(CI^2-IN^2\right)\)
\(=BI^2-CI^2=BI^2-AI^2=BA^2\)
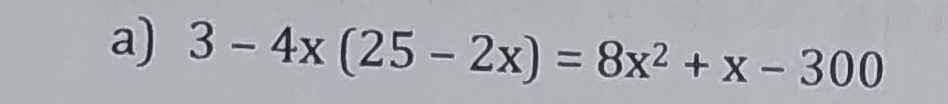
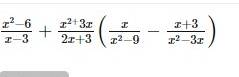 giúp tui zới mn oi bí quá
giúp tui zới mn oi bí quá