29-109=? HIHIHIHI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực


MD
0


8 tháng 11 2021
539675839865548654654565785 - 4859499386948569498349865743 = -4.3198235e+27
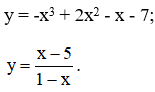 các bạn nào lớp 1 đến 11 thì không nên làm nhé
các bạn nào lớp 1 đến 11 thì không nên làm nhé
đáp án -80 nha bn
80 nha bởi vì 29-109=109 - 29 80