đến năm 2006, số dân của phường đó là:

15.500 x (100% + 1,2%) = 15686 (người)

Bài 5:

a: Diện tích xung quanh là:

\(\left(4,5+2,5\right)\times2\times1,8=25,2\left(m^2\right)\)

Diện tích toàn phần là:

25,2+4,5x2,5=36,45(m²)

b: Thể tích nước tối đa bể có thể chứa được là:

4,5x2,5x1,8=20,25(m³)=20250(lít)

c: Chiều cao hiện tại của mực nước là:

16,2:4,5:2,5=1,44(m)

\(P\left(x\right)=x^{2023}-2022x^{2022}-2022x^{2021}-\dots-2022x^2-2022x+1\)

\(\Rightarrow P\left(2023\right)=2023^{2023}-2022\cdot2023^{2022}-2022\cdot2023^{2021}-\dots-2022\cdot2023^2-2022\cdot2023+1\)

\(=2023^{2023}-\left(2023-1\right)\cdot2023^{2022}-\left(2023-1\right)\cdot2023^{2021}-\dots-\left(2023-1\right)\cdot2023^2-\left(2023-1\right)\cdot2023+1\)

\(=2023^{2023}-2023^{2023}+2023^{2022}-2023^{2022}+2023^{2021}-\dots-2023^3+2023^2-2023^2+2023+1\)

\(=2024\)

___

Cách giải: Tách các hệ số để làm xuất hiện các lũy thừa của \(2023\)

 Ta thấy:    \(x=2023\Rightarrow x-1=2022\) 

Ta có:

\(P\left(x\right)=x^{2023}-\left(x-1\right)\times x^{2022}-\left(x-1\right)\times x^{2021}-...-\left(x-1\right)\times x^2-\left(x-1\right)\times x+1\)\(P\left(x\right)=x^{2023}-x^{2023}+x^{2022}-x^{2022}+x^{2021}-....-x^3+x^2-x^2+x+1\)

\(P\left(x\right)=x+1\)

Thay x=2023, ta có:

\(P\left(2023\right)=2023+1=2024\)

Bài 1:

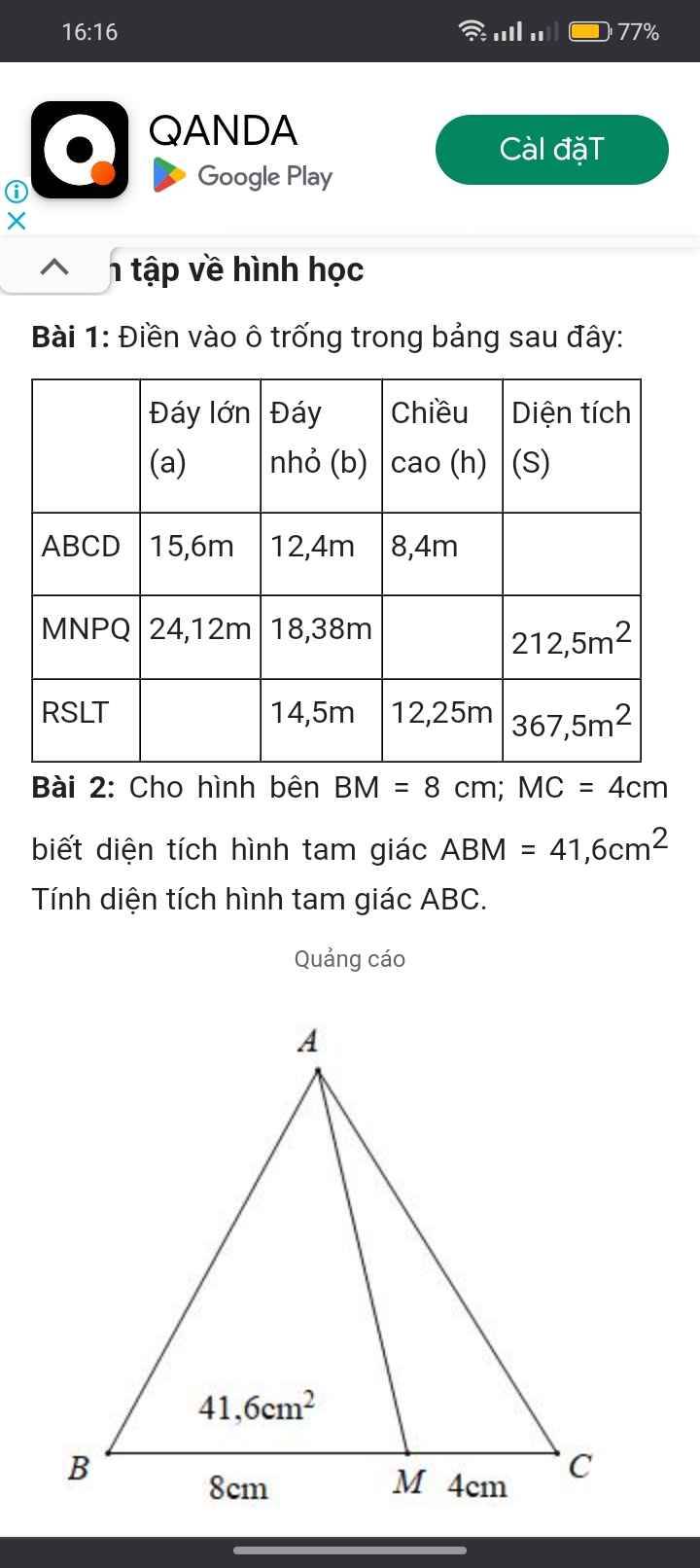
Bài 2:

Chiều cao tam giác ABM (hay cũng là chiều cao tam giác ABC) là:

$41,6\times 2:8=10,4$ (cm)

Diện tích tam giác $ABC$ là:

$10,4\times (8+4):2=62,4$ (cm²)

giúp mình với mình đang cần gấp

Bài 3:

112,4x10=1124

68,3x100=6830

4,351x1000=4351

112,4x0,1=11,24

68,3x0,01=0,683

4,351x0,001=0,004351

Bài 1:

a: \(\dfrac{3}{4}+\dfrac{2}{3}=\dfrac{9}{12}+\dfrac{8}{12}=\dfrac{17}{12}\)

\(\dfrac{3}{5}+\dfrac{7}{10}=\dfrac{6}{10}+\dfrac{7}{10}=\dfrac{13}{10}\)

\(\dfrac{2}{9}+\dfrac{1}{5}+\dfrac{7}{9}+\dfrac{4}{5}=\left(\dfrac{2}{9}+\dfrac{7}{9}\right)+\left(\dfrac{1}{5}+\dfrac{4}{5}\right)=1+1=2\)

b: \(\dfrac{2}{3}-\dfrac{2}{7}=\dfrac{14}{21}-\dfrac{6}{21}=\dfrac{8}{21}\)

\(\dfrac{3}{4}-\dfrac{5}{12}=\dfrac{9}{12}-\dfrac{5}{12}=\dfrac{4}{12}=\dfrac{1}{3}\)

\(\dfrac{5}{12}+\dfrac{5}{6}-\dfrac{3}{4}=\dfrac{5}{12}+\dfrac{10}{12}-\dfrac{9}{12}=\dfrac{6}{12}=\dfrac{1}{2}\)

c: \(\dfrac{2}{5}\times\dfrac{3}{7}=\dfrac{2\times3}{5\times7}=\dfrac{6}{35}\)

\(\dfrac{4}{9}\times\dfrac{3}{10}=\dfrac{4\times3}{9\times10}=\dfrac{12}{90}=\dfrac{2}{15}\)

\(\dfrac{1}{3}\times\dfrac{3}{5}\times\dfrac{5}{9}=\dfrac{1\times3\times5}{3\times5\times9}=\dfrac{15}{135}=\dfrac{1}{9}\)

d: \(\dfrac{7}{8}:2=\dfrac{7}{8\times2}=\dfrac{7}{16}\)

\(\dfrac{3}{8}:\dfrac{7}{5}=\dfrac{3}{8}\times\dfrac{5}{7}=\dfrac{15}{56}\)

\(\dfrac{15}{16}:\dfrac{3}{8}\times\dfrac{3}{4}=\dfrac{15}{16}\times\dfrac{8}{3}\times\dfrac{3}{4}=\dfrac{15\times8\times3}{16\times3\times4}=\dfrac{360}{192}=\dfrac{15}{8}\)

\(\left(\dfrac{7}{12}+\dfrac{5}{9}\times\dfrac{3}{8}\right):\dfrac{19}{15}\)

\(=\left(\dfrac{7}{12}+\dfrac{15}{72}\right):\dfrac{19}{15}\)

\(=\left(\dfrac{42}{72}+\dfrac{15}{72}\right):\dfrac{19}{15}\)

\(=\dfrac{57}{72}\times\dfrac{15}{19}=\dfrac{57}{19}\times\dfrac{15}{72}=3\times\dfrac{5}{24}=\dfrac{15}{24}=\dfrac{5}{8}\)

Chiều dài thửa ruộng:

100 : 2/3 = 150 (m)

Diện tích thửa ruộng:

150 × 100 = 15000 (m²)

a) Thể tích viên gạch:

2 × 2 × 2 = 8 (dm³)

Thể tích lòng bể:

8 × 500 = 4000 (dm³)

b) Mỗi giờ, tổng thể tích nước hai vòi chảy vào bể:

2600 + 2400 = 5000 (l)

Thời gian để hai vòi chảy đầy bể:

4000 : 5000 = 0,8 (giờ) = 48 (phút)

Phải là hỏi độ dài quãng đường AB là bao nhiêu km chứ bạn?

Lời giải:

Thời gian ô tô đi quãng đường AB (không kể thời gian nghỉ) là:
9 giờ 50 phút - 7 giờ 15 phút - 20 phút = 2 giờ 15 phút = 2,25 giờ

Độ dài quãng đường AB:

$64\times 2,25=144$ (km)