
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1B:
a)
\(\dfrac{-1}{16}+\dfrac{-1}{24}\\ =\dfrac{-3}{48}+\dfrac{-2}{48}\\ =\dfrac{-5}{48}\)
b)
\(\dfrac{-1}{8}-\dfrac{3}{20}\\ =\dfrac{-5}{40}-\dfrac{6}{40}\\ =\dfrac{-11}{40}\)
c)
\(-\dfrac{18}{10}+0,4\\ =\dfrac{-9}{5}+\dfrac{2}{5}\\ =\dfrac{-7}{5}\)
d)
\(6,5-\left(-\dfrac{1}{5}\right)\\ =\dfrac{13}{2}+\dfrac{1}{5}\\ =\dfrac{65}{10}+\dfrac{2}{10}\\ =\dfrac{67}{10}\)

Đây là toán nâng cao chuyên đề phân số, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp giải ngược như sau:
Giải:
Nếu lần thứ ba người đó chỉ bán \(\dfrac{1}{2}\) số cam còn lại mà không bán thêm 1 quả thì số cam còn lại sau khi bán là:
10 + 1 = 11 (quả)
11 quả ứng với phân số là:
1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\) (số cam còn lại sau lần bán thứ hai)
Số cam còn lại sau lần bán thứ hai là:
11 : \(\dfrac{1}{2}\) = 22 (quả)
Nếu lần thứ hai người đó chỉ bán \(\dfrac{1}{2}\) số cam còn lại mà không bán thêm 1 quả thì sau khi bán còn lại số cam là:
22 + 1 = 23 (quả)
23 quả ứng với số cam là:
1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\) (số cam còn lại sau lần bán thứ nhất)
Số cam còn lại sau lần bán thứ nhất là:
23 : \(\dfrac{1}{2}\) = 46 (quả)
Nếu lần thứ nhất người đó chỉ bán \(\dfrac{1}{2}\) số cam và không bán thêm 1 quả thì số cam còn lại sau lần bán thứ nhất là:
46 + 1 = 47 (quả)
47 quả ứng với phân số là:
1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\) (số cam)
Ban đầu người đó có số cam là"
47 : \(\dfrac{1}{2}\) = 94 (quả)
Đáp số:...
1/2 số quả cam còn lại sau lần bán thứ hai là:
10+1=11(quả)
Số quả cam còn lại sau khi bán lần 2 là \(11:\dfrac{1}{2}=22\left(quả\right)\)
1/2 số quả cam còn lại sau khi bán lần thứ nhất là:
22+1=23(quả)
Số quả cam còn lại sau khi bán lần thứ nhất là:
\(23:\dfrac{1}{2}=46\left(quả\right)\)
Số quả cam ban đầu là:
\(\left(46+1\right):\dfrac{1}{2}=94\left(quả\right)\)

Các phương trình bậc nhất 2 ẩn là: `3x-y=3;x+2y=8;y+3y=11`
Hệ số a,b,c của các pt là:
+) `3x-y=3` có `a=3; b=-1;c=3`
+) `x+2y=8` có `a=1;b=2;c=8`
+) `y+3x=11` có `a=3;b=1;c=11`

Vì em cần gấp nên chị sẽ tham khảo nhanh nhé:
Có 66 số chia hết cho 3 nhỏ hơn 200 là 3, 6, ..., 198.
Tổng các số này là (3 + 198) × 66 : 2 = 6633.
Có 39 số chia hết cho 5 nhỏ hơn 200 là 5, 10, ...,195.
Tổng các số này là (5 + 195) × 39 : 2 = 3900.
Có 13 số chia hết cho cả 3 và 5 là 15, 30, ..., 195.
Tổng các số này là (15 + 195) × 13 : 2 = 1365.
Tổng các số theo yêu cầu đề bài là
6633 + 3900 – 1365 = 9168.

Câu 3:
12 + x = 23
x = 23 - 12
x = 11
_____
x : 14 = 1234 + 2314
x : 14 = 3548
x = 49672
Câu 1:
176234 + 341257 + 21
= 517491 + 21
= 517512
Chọn C. 517512

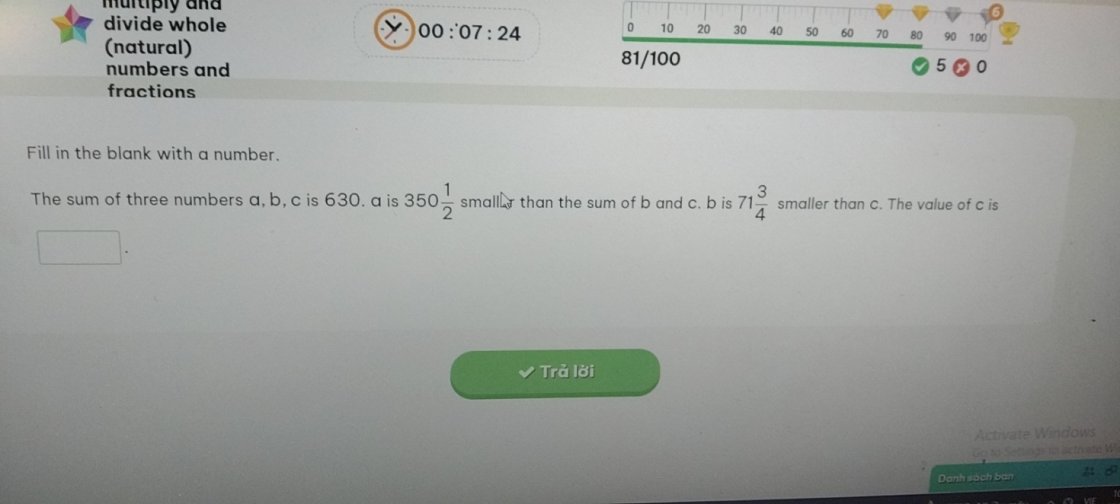
Tổng của ba số a; b; c là 630
a nhỏ hơn tổng của hai số b và c là 350\(\dfrac{1}{2}\)
b nhỏ hơn c là 71\(\dfrac{3}{4}\)
Tìm giá trị của c

Đổi \(435dm^3=435l\)
Thể tích nước trong bể là:
\(435\text{}\times75\%=326,25\) (l nước)
Đáp số: 326,25 l nước

8)
a) Tam giác ABI và ACK có:
\(\widehat{AIB}=\widehat{AKC}=90^o;\widehat{BAC}\) chung
\(\Rightarrow\Delta ABI\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AI}{AK}\)
\(\Rightarrow\dfrac{AK}{AC}=\dfrac{AI}{AB}\)
Tam giác AIK và ABC có:
\(\dfrac{AK}{AC}=\dfrac{AI}{AB};\widehat{BAC}\) chung
\(\Rightarrow\Delta AIK\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{S_{AIK}}{S_{ABC}}=\left(\dfrac{AI}{AB}\right)^2=cos^2A\)
\(\Rightarrow S_{AIK}=S_{ABC}.cos^2A\)
b) Có \(S_{BCIK}=S_{ABC}-S_{AIK}\)
\(=S_{ABC}-S_{ABC}.cos^2A\)
\(=S_{ABC}\left(1-cos^2A\right)\)
\(=S_{ABC}.sin^2A\)
c) \(S_{HIK}=S_{ABC}-S_{AKI}-S_{BHK}-S_{CHI}\)
\(=S_{ABC}-S_{ABC}.cos^2A-S_{ABC}.cos^2B-S_{ABC}.cos^2C\)
\(=S_{ABC}\left(1-cos^2A-cos^2B-cos^2C\right)\)
d) Có \(cotB=\dfrac{BH}{AH};cotC=\dfrac{CH}{AH}\)
\(\Rightarrow cotB+cotC=\dfrac{BH}{AH}+\dfrac{CH}{AH}=\dfrac{BC}{AH}\)
Nếu \(cotB+cotC\ge\dfrac{2}{3}\) thì \(\dfrac{BC}{AH}\ge\dfrac{2}{3}\Leftrightarrow BC\ge\dfrac{2}{3}AH\)
Nhưng điều này chưa chắc đã đúng tùy vào cách vẽ hình nên bạn cần bổ sung thêm điều kiện gì đó vào câu này nhé.


2B:
a) C1: \(\dfrac{-7}{12}=\dfrac{-6-1}{12}=\dfrac{-6}{12}+\dfrac{-1}{12}=\dfrac{-1}{2}+\dfrac{-1}{12}\)
C2: \(\dfrac{-7}{12}=\dfrac{-3-4}{12}=\dfrac{-3}{12}+\dfrac{-4}{12}=\dfrac{-1}{4}+\dfrac{-1}{3}\)
C4: \(\dfrac{-7}{12}=\dfrac{-2-5}{12}=\dfrac{-2}{12}+\dfrac{-5}{12}\)
b) C1: \(\dfrac{-7}{12}=\dfrac{4-11}{12}=\dfrac{4}{12}-\dfrac{11}{12}=\dfrac{1}{3}-\dfrac{11}{12}\)
C2: \(\dfrac{-7}{12}=\dfrac{2-9}{12}=\dfrac{2}{12}-\dfrac{9}{12}=\dfrac{1}{6}-\dfrac{3}{4}\)
C3: \(\dfrac{-7}{12}=\dfrac{3-10}{12}=\dfrac{3}{12}-\dfrac{10}{12}=\dfrac{1}{4}-\dfrac{5}{6}\)