43-28=?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


200x53+47x156+47x44
\(=200\cdot53+47\cdot\left(156+44\right)\)
\(=53\cdot200+47\cdot200=200\cdot\left(53+47\right)\)
\(=200\cdot100=20000\)

a: Ta có: \(AK=KB=\dfrac{AB}{2}\)
\(DI=IC=\dfrac{DC}{2}\)
mà AB=CD
nên AK=KB=DI=IC
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AI//CK và AI=CK
b: Xét ΔDNC có
I là trung điểm của DC
IM//NC
Do đó: M là trung điểm của DN
=>DM=MN
Xét ΔBAM có
K là trung điểm của BA
KN//AM
Do đó: N là trung điểm của BM
=>BN=NM
=>BN=NM=DM
c: Xét tứ giác BKDI có
BK//DI
BK=DI
Do đó: BKDI là hình bình hành
=>DK//BI
=>EK//FI
ta có: AI//CK
=>IE//KF
Xét tứ giác EKFI có
EK//FI
EI//KF
Do đó: EKFI là hình bình hành



a, \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow cosx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=-\dfrac{3}{5}:\left(\dfrac{4}{5}\right)=-\dfrac{3}{4}\)
\(cotx=-\dfrac{4}{3}\)
c, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=\dfrac{3}{4}\)
b, \(cos^2x+sin^2x=1\Leftrightarrow sin^2x=1-\dfrac{1}{16}=\dfrac{15}{16}\Leftrightarrow sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{\sqrt{15}}\)
d, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{25}{169}=\dfrac{144}{169}\Leftrightarrow sinx=\dfrac{12}{13}\)
\(tanx=\dfrac{12}{13}:\left(-\dfrac{5}{13}\right)=-\dfrac{12}{5}\)
\(cotx=-\dfrac{5}{12}\)
a: \(\Omega< x< \dfrac{3}{2}\Omega\)
=>cosx<0
Ta có: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}\)
mà cosx<0
nên \(cosx=-\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-3}{5}:\dfrac{-4}{5}=\dfrac{3}{4}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{4}{3}\)
b: \(0< x< \dfrac{\Omega}{2}\)
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà sin x>0
nên \(sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{1}{\sqrt{15}}=\dfrac{\sqrt{15}}{15}\)
c: 0<x<90 độ
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}=\left(\dfrac{4}{5}\right)^2\)
mà sin x>0
nên \(sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=1:\dfrac{4}{3}=\dfrac{3}{4}\)
d: \(180^0< x< 270^0\)
=>sin x<0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(-\dfrac{5}{13}\right)^2=1-\dfrac{25}{169}=\dfrac{144}{169}\)
mà sin x<0
nên \(sinx=-\dfrac{12}{13}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-12}{13}:\dfrac{-5}{13}=\dfrac{12}{5}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{5}{12}\)

a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔABH~ΔCBA
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{6}=\dfrac{CD}{10}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{5}\)
mà AD+CD=AC=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{8}{8}=1\)
=>\(AD=3\cdot1=3\left(cm\right);CD=5\cdot1=5\left(cm\right)\)
c:
ΔBAD vuông tại A
=>\(S_{BAD}=\dfrac{1}{2}\cdot BA\cdot AD=\dfrac{1}{2}\cdot6\cdot3=9\left(cm^2\right)\)
ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
Xét ΔBAD vuông tại A và ΔBHI vuông tại H có
\(\widehat{ABD}=\widehat{HBI}\)
Do đó: ΔBAD~ΔBHI
=>\(\dfrac{S_{BAD}}{S_{BHI}}=\left(\dfrac{BA}{BH}\right)^2=\left(\dfrac{5}{3}\right)^2=\dfrac{25}{9}\)
=>\(S_{BHI}=S_{BAD}\cdot\dfrac{9}{25}=\dfrac{81}{25}\left(cm^2\right)\)

Tỉ số giữa số vải còn lại sau buổi sáng so với ban đầu là:
\(1-\dfrac{3}{11}=\dfrac{8}{11}\)
Tỉ số giữa số vải còn lại sau buổi chiều so với ban đầu là:
\(\dfrac{8}{11}\times\left(1-\dfrac{3}{8}\right)=\dfrac{8}{11}\times\dfrac{5}{8}=\dfrac{5}{11}\)
Độ dài tấm vải đó là:
\(16:\dfrac{5}{11}=16\times\dfrac{11}{5}=35,2\left(m\right)\)
Buổi sáng bán được:
\(35,2\times\dfrac{3}{11}=9,6\left(m\right)\)
Buổi chiều bán được:
35,2-9,6-16=9,6(m)
Số vải còn lại sau khi bán vào buổi sáng là:
\(1-\dfrac{3}{11}=\dfrac{8}{11}\) (tấm vải)
Số vải bán vào buổi chiều là:
\(\dfrac{8}{11}\times\dfrac{3}{8}=\dfrac{3}{11}\) (tấm vải)
Số vải còn lại sau khi bán vào buổi chiều là:
\(\dfrac{8}{11}-\dfrac{3}{11}=\dfrac{5}{11}\) (tấm vải)
Số mét vải ban đầu là:
\(16:\dfrac{5}{11}=35,2\) (m)
Số mét vải bán vào buổi sáng là:
\(35,2\times\dfrac{3}{11}=9,6\) (m)
Số mét vải bán vào buổi chiều là:
\(35,2\times\dfrac{3}{11}=9,6\) (m)
Đáp số:...


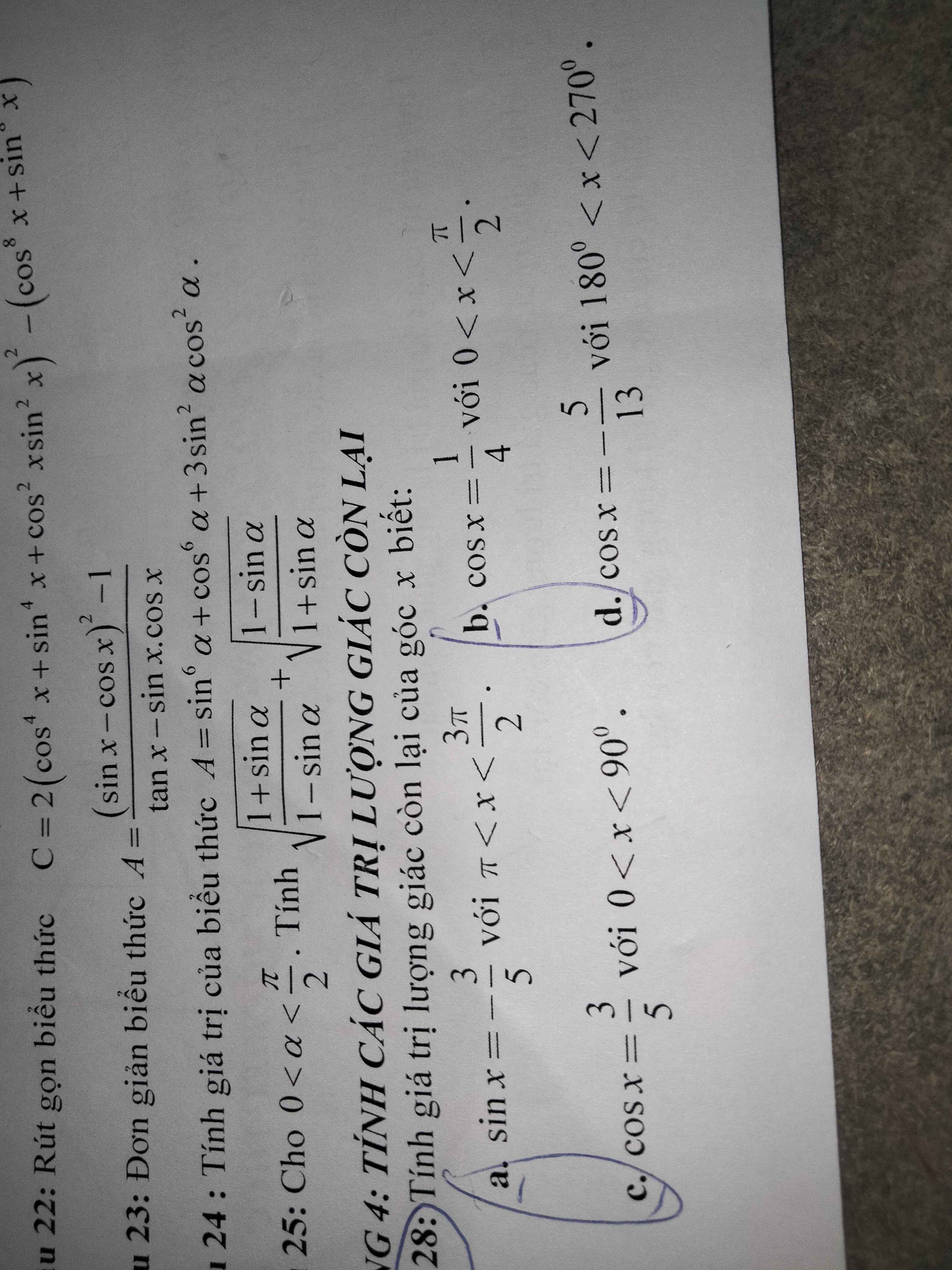

43 - 28 = 15
15