giải giúp mình nhanh nha cảm ơn nhiều💕💕
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng vận tốc của 2 xe là:
142 + 58 = 200 ( km/h )
2 xe gặp nhau sau thời gian là:
168 : 200 = 0,84 ( giờ )
Đáp số: 0,84 giờ
* Bạn kiểm tra lại đề xem có nhầm ở đâu không tại vì thường không có ô tô nào đi trên đường với vận tốc 142 km/h cả ( ngoại trừ đường cao tốc nhưng thường thì xe máy không đi trên đường cao tốc ).

\(B=x^{15}-8x^{14}+8x^3-8x^2+...-8x^2+8x-5\)
Vì \(x=7\) nên
\(x+1=8\)
\(B=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^3-\left(x+1\right)x^2+...-\left(x+1\right)x^2+\left(x+1\right)x-5\)
\(B=x^{15}-x^{15}-x^{14}+x^{14}+x^3-x^3-x^2+...-x^2+x^2+x-5\)
\(B=x-5\)
\(B=>7-5=2\)
Vậy \(B=2\)

\(A=\dfrac{3.5.7.11.13.37-10101}{1212120+40404}\)
\(A=\dfrac{5.11.3.7.11.13-3.7.11.13}{120.10101+4.10101}\)
\(A=\dfrac{3.7.11.13.\left(5.11-1\right)}{10101\cdot\left(120+4\right)}\)
\(A=\dfrac{10101.54}{10101.124}\)
\(A=\dfrac{54}{124}=\dfrac{27}{62}\)
\(\Rightarrow\) Vậy \(A=\dfrac{27}{62}\)

Bốn năm nữa số tuổi của cha hơn số tuổi của con 30 tuổi
Hiệu số phần bằng nhau:
3 - 1 = 2 (phần)
Tuổi của con sau 4 năm:
30 : 2 × 1 = 15 (tuổi)
Tuổi con hiện nay:
15 - 4 = 11 (tuổi)

Chiều cao tăng thêm khi thả hòn non bộ:
47 - 35 = 12 (cm) = 0,12 (m)
Thể tích hòn non bộ:
1,2 × 0,4 × 0,12 = 0,576 (m³)
Chọn A
D bạn nhé
B1: bn tính thể tích khi cho hòn non bộ vào
B2: bn tính thế tích khi chưa cho hòn non bộ vào
B3: lấy cái đầu trừ đi

Bài 2
a) 5/3 - x = 2 1/3
5/3 - x = 7/3
x = 5/3 - 7/3
x = -2/3
b) 3,5 - 1/2 x = -5/4
1/2 x = 3,5 - (-5/4)
1/2 x = 19/4
x = 19/4 : 1/2
x = 19/2
c) 4/(2 - x) - 2/3 = 0
4/(2 - x) = 2/3
2(2 - x) = 3.4
2(2 - x) = 12
2 - x = 12 : 2
2 - x = 6
x = 2 - 6
x = -4
d) 0,25 + 7,5% x = 2 5/6
3/40 x = 17/6 - 0,25
3/40 x = 31/12
x = 31/12 : 3/40
x = 310/9
Bài 4
a) Số học sinh xếp loại tốt:
120 . 4/15 = 32 (học sinh)
Số học sinh xếp loại khá:
32 : 80% = 40 (học sinh)
Số học sinh xếp loại đạt:
120 - 32 - 40 = 48 (học sinh)
b) Tỉ số phần trăm của số học sinh xếp loại khá so với cả khối:
40 . 100% : 120 ≈ 33,33%

Điều kiện:
\(\left\{{}\begin{matrix}x+\dfrac{3}{x}=\dfrac{x^2+3}{x}\ge0\\\dfrac{x^2+7}{2\left(x+1\right)}\ge0\end{matrix}\right.\)
mà \(x^2\ge0\forall x\Rightarrow\left\{{}\begin{matrix}x^2+3>0\forall x\\x^2+7>0\forall x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x^2+3}{x}\ge0\\\dfrac{x^2+7}{2\left(x+1\right)}\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>0\\2\left(x+1\right)>0\Leftrightarrow x+1>0\Leftrightarrow x>-1\end{matrix}\right.\)
\(\Leftrightarrow x>0\)
\(\sqrt{x+\dfrac{3}{x}}=\dfrac{x^2+7}{2\left(x+1\right)}\)
\(\Leftrightarrow\sqrt{\dfrac{x^2+3}{x}}=\dfrac{x^2+7}{2\left(x+1\right)}\)
\(\Leftrightarrow\left(\sqrt{\dfrac{x^2+3}{x}}\right)^2=\left[\dfrac{x^2+7}{2\left(x+1\right)}\right]^2\)
\(\Leftrightarrow\dfrac{x^2+3}{x}=\dfrac{\left(x^2+7\right)^2}{\left[2\left(x+1\right)\right]^2}\)
\(\Leftrightarrow\dfrac{x^2+3}{x}=\dfrac{x^4+14x^2+49}{4\left(x+1\right)^2}=\dfrac{x^4+14x^2+49}{4\left(x^2+2x+1\right)}=\dfrac{x^4+14x^2+49}{4x^2+8x+4}\)
\(\Leftrightarrow\dfrac{\left(x^2+3\right)\left(4x^2+8x+4\right)}{x\left(4x^2+8x+4\right)}=\dfrac{x\left(x^4+14x^2+49\right)}{x\left(4x^2+8x+4\right)}\)
\(\Leftrightarrow\left(x^2+3\right)\left(4x^2+8x+4\right)=x\left(x^4+14x^2+49\right)\)
\(\Leftrightarrow x^2\left(4x^2+8x+4\right)+3\left(4x^2+8x+4\right)=x\left(x^4+14x^2+49\right)\)
\(\Leftrightarrow4x^4+8x^3+4x^2+12x^2+24x+12=x^5+14x^3+49x\)
\(\Leftrightarrow4x^4+8x^3+16x^2+24x+12=x^5+14x^3+49x\)
\(\Leftrightarrow x^5-4x^4+14x^3-8x^3-16x^2+49x-24x-12=0\)
\(\Leftrightarrow x^5-4x^4+6x^3-16x^2+25x-12=0\)
\(\Leftrightarrow x^5-x^4-3x^4+3x^3+3x^3-3x^2-13x^2+13x+12x-12=0\)
\(\Leftrightarrow x^4\left(x-1\right)-3x^3\left(x-1\right)+3x^2\left(x-1\right)-13x\left(x-1\right)+12\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^4-3x^3+3x^2-13x+12\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^4-x^3-2x^3+2x^2+x^2-x-12x+12\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^3\left(x-1\right)-2x^2\left(x-1\right)+x\left(x-1\right)-12\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-1\right)\left(x^3-2x^2+x-12\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^3-2x^2+x-12\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^3-3x^2+x^2-3x+4x-12\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left[x^2\left(x-3\right)+x\left(x-3\right)+4\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x-3\right)\left(x^2+x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\\x^2+x+4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=3\left(tm\right)\\x^2+x+\dfrac{1}{4}+\dfrac{15}{4}=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=3\left(tm\right)\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{15}{4}=0\end{matrix}\right.\)
Có: \(\left(x+\dfrac{1}{2}\right)^2\ge0\forall x\Rightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{15}{4}>0\forall x\)
\(\Rightarrow x^2+x+4=0\) vô nghiệm
Vậy: \(x\in\left\{1;3\right\}\)


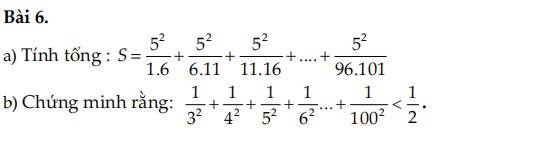

a: \(A=\dfrac{2x^2-4x+7}{x^2-2x+2}\)
\(=\dfrac{2x^2-4x+4+3}{x^2-2x+2}\)
\(=2+\dfrac{3}{x^2-2x+2}=2+\dfrac{3}{\left(x-1\right)^2+1}\)
\(\left(x-1\right)^2+1>=1\forall x\)
=>\(\dfrac{3}{\left(x-1\right)^2+1}< =\dfrac{3}{1}=3\forall x\)
=>\(A=\dfrac{3}{\left(x-1\right)^2+1}+2< =3+2=5\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1