8 + 800 + 80

= 888

Chọn B.888

B

 Đây  là toán nâng cao cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp khử như sau:

                                     Giải:

50% số học sinh lớp 5A và 50% số học sinh lớp 5B là:

           72 x 50 : 100 = 36 (học sinh)

44 học sinh hơn 36 học sinh là: 44 - 36 = 8 (học sinh)

8 học sinh ứng với: 70% - 50% =  20% (số học sinh lớp 5A)

Số học sinh lớp 5A là: 8 : 20 x 100 = 40 (học sinh)

Đáp số: 40 học sinh

a: Trên tia Ox, ta có: OM<ON

nên M nằm giữa O và N

b: Ta có: M nằm giữa O và N

=>OM+MN=ON

=>MN+6=12

=>MN=6(cm)

c: Sửa đề: M có phải là trung điểm của ON không

Ta có: M nằm giữa O và N

mà MO=MN(=6cm)

nên M là trung điểm của ON

Em cần làm gì với biểu thức này!

giúp mình với

Gọi số vở mà ba bạn A,B,C đã mua lần lượt là a(quyển),b(quyển),c(quyển)

(Điều kiện: \(a,b,c\in Z^+\))

2/3 số vở của học sinh A bằng số vở của học sinh B bằng 2/5 số vở của học sinh C

=>\(\dfrac{2}{3}a=b=\dfrac{2}{5}c\)

=>\(\dfrac{a}{1,5}=\dfrac{b}{1}=\dfrac{c}{2,5}\)

Tổng số vở là 120 nên a+b+c=120

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{1,5}=\dfrac{b}{1}=\dfrac{c}{2,5}=\dfrac{a+b+c}{1,5+1+2,5}=\dfrac{120}{5}=24\)

=>\(a=24\cdot1,5=36\left(nhận\right);b=24\cdot1=24\left(nhận\right);c=24\cdot2,5=60\left(nhận\right)\)

vậy: A mua 36 quyển; B mua 24 quyển; C mua 60 quyển

Cái  thì tui chịu

Sửa đề:

ABC cân tại A có BH và CK là hai đường cao

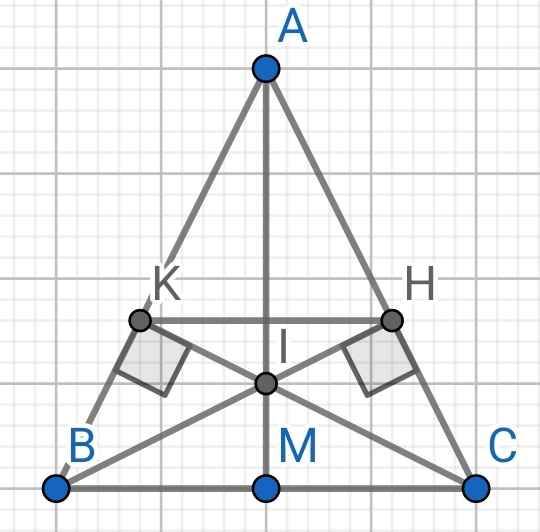
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆AHB và ∆AKC có:

AB = AC (cmt)

∠A chung

⇒ ∆AHB = ∆AKC (cạnh huyền - góc nhọn)

⇒ AH = AK (hai cạnh tương ứng)

⇒ ∆AKH cân tại A

b) ∆ABC cân tại A (gt)

BH và CK là hai đường cao cắt nhau tại I (gt)

⇒ AI là đường cao thứ ba

⇒ AI ⊥ BC

⇒ IM ⊥ BC

Do ∆ABC cân tại A có

AI là đường cao (cmt)

⇒ AM là đường cao

⇒ AM cũng là đường trung tuyến

⇒ M là trung điểm của BC

⇒ MB = MC

Xét hai tam giác vuông: ∆IBM và ∆ICM có:

IM là cạnh chung

MB = MC (cmt)

⇒ ∆IBM = ∆ICM (hai cạnh góc vuông)

⇒ ∠BIM = ∠CIM (hai góc tương ứng)

⇒ IM là tia phân giác của ∠BIC

c) Xét hai tam giác vuông: ∆AHI và ∆AKI có:

AI là cạnh chung

AH = AK (cmt)

⇒ ∆AHI = ∆AKI (cạnh huyền - cạnh góc vuông)

⇒ IH = IK (hai cạnh tương ứng)

⇒ I nằm trên đường trung trực của HK (1)

Do AH = AK (cmt)

⇒ A nằm trên đường trung trực của HK (2)

Từ (1) và (2) ⇒ AI là đường trung trực của HK

⇒ AI ⊥ HK

Lại có:

AI ⊥ BC (cmt)

⇒ HK // BC

Chu vi của cái sân hình vuông là:

78 + (3 + 8) x 2 = 100 (m)

Cạnh của cái sân hình vuông là:

  100 : 4  =  25 (m)

Chiều dài của cái sân hình chữ nhật ban đầu là:

   25 - 3 = 22 (m)

Chiều rộng của cái sân hình chữ nhật ban đầu là:

  25 - 8 = 17 (m)

Em cần tính diện tích của sân bóng lúc đầu hay lúc sau?

a: Ta có: \(\widehat{AOC}+\widehat{BOC}=180^0\)(hai góc kề bù)

\(\widehat{AOC}-\widehat{BOC}=80^0\)

Do đó: \(\widehat{AOC}=\dfrac{180^0+80^0}{2}=130^0\); \(\widehat{BOC}=130^0-80^0=50^0\)

b: \(5\cdot\widehat{AOC}=7\cdot\widehat{BOC}\)

=>\(\widehat{AOC}=\dfrac{7}{5}\cdot\widehat{BOC}\)

Ta có: \(\widehat{AOC}+\widehat{BOC}=180^0\)(hai góc kề bù)

=>\(\dfrac{7}{5}\cdot\widehat{BOC}+\widehat{BOC}=180^0\)

=>\(\dfrac{12}{5}\cdot\widehat{BOC}=180^0\)

=>\(\widehat{BOC}=180^0:\dfrac{12}{5}=75^0\)

=>\(\widehat{AOC}=180^0-75^0=105^0\)

Bài 1:

a: D

b: B

c: C

d: B

Bài 2:

a: 7,1>7,08

b: 42,090=42,09

c: 18,279<18,28

d: 0,48>0,4799

Bài 3:

a: S

b: Đ

c: Đ

d: S

Bài 1

a) Đề sai, nếu đề đúng thì chọn câu D

b) B

c) D

d) B